
Question Number 24569 by ajfour last updated on 21/Nov/17

Commented by ajfour last updated on 21/Nov/17

$${In}\:{a}\:{gravity}\:{free}\:{cubical}\:{box},\:{a} \\ $$$${ball}\:{bounces}\:{elastically}.\:{If}\:{it}\:{be} \\ $$$${projected}\:{from}\:{origin}\:{O}\:{towards} \\ $$$${A}\left(\mathrm{4},\:\mathrm{13},\:\mathrm{16}\right),\:{a}\:{point}\:{on}\:{the}\:{roof} \\ $$$${plane}\:{then}\:{find}\:{the}\:{second}\:{and} \\ $$$${third}\:{bounce}\:{points}\:\boldsymbol{{B}},\:\boldsymbol{{C}}\:. \\ $$$${The}\:{edge}\:{length}\:{of}\:{the}\:{cube}\:{is} \\ $$$$\mathrm{16}\:{units}. \\ $$
Commented by ajfour last updated on 22/Nov/17
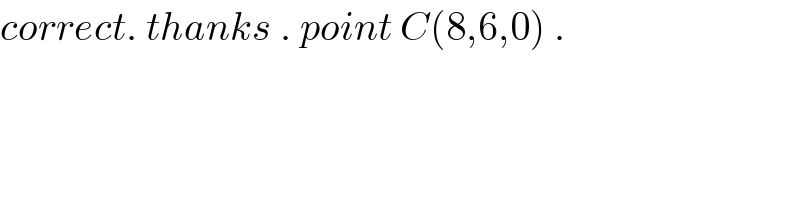
$${correct}.\:{thanks}\:.\:{point}\:{C}\left(\mathrm{8},\mathrm{6},\mathrm{0}\right)\:. \\ $$
Commented by jota last updated on 21/Nov/17

$${B}\:{esta}\:{en}\:{el}\:{plano}\:{y}=\frac{\mathrm{13}}{\mathrm{4}}{x} \\ $$$$\:\Rightarrow\mathrm{16}=\frac{\mathrm{13}}{\mathrm{4}}{x}_{{B}} \\ $$$${En}\:{ese}\:{plano}\:{por}\:{semejanza}\:{de} \\ $$$$\:{triangulos} \\ $$$$\frac{\mathrm{16}}{\mathrm{13}}=\frac{\mathrm{16}−{z}_{{B}} }{\mathrm{3}} \\ $$$$\Rightarrow{B}\left(\frac{\mathrm{64}}{\mathrm{13}}\:\:\:\mathrm{16}\:\:\mathrm{12}\frac{\mathrm{4}}{\mathrm{13}}\right) \\ $$$$ \\ $$
Answered by mrW1 last updated on 22/Nov/17
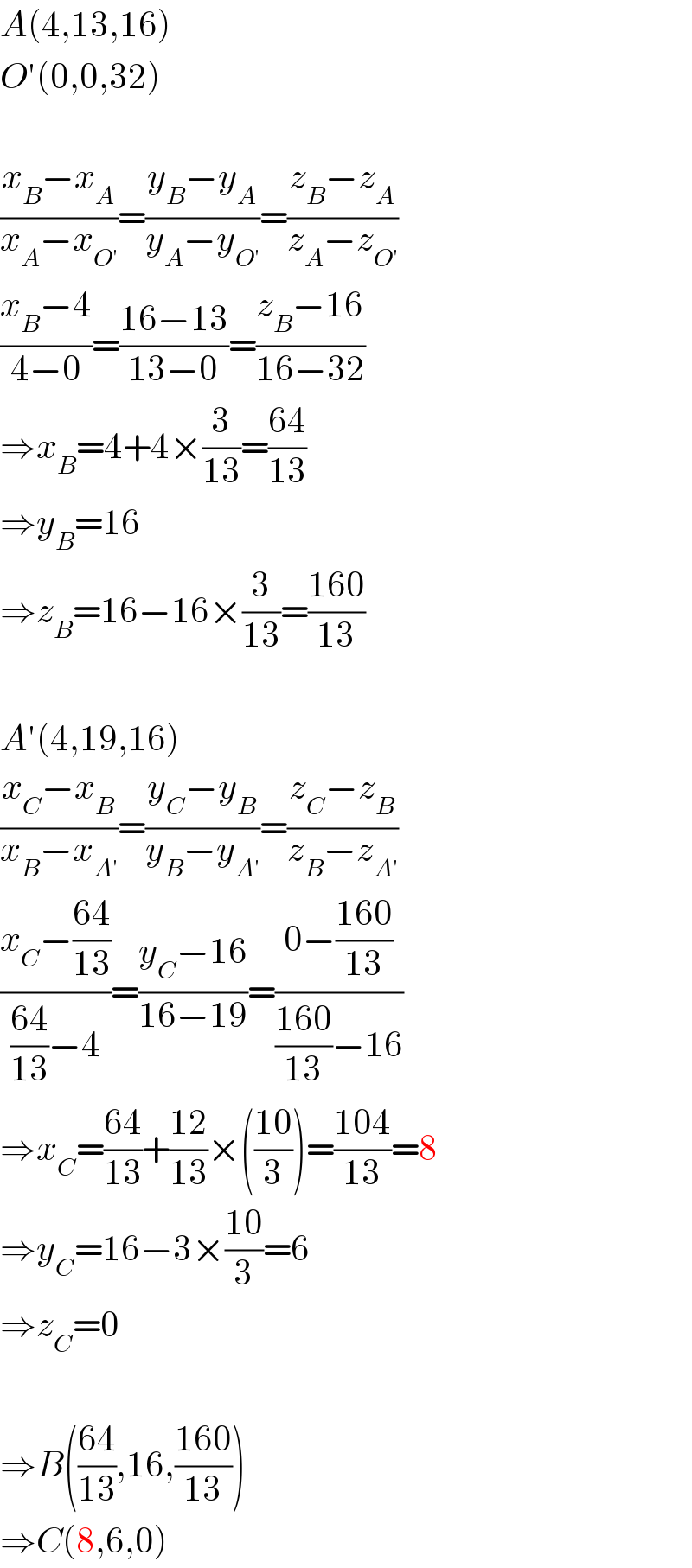
$${A}\left(\mathrm{4},\mathrm{13},\mathrm{16}\right) \\ $$$${O}'\left(\mathrm{0},\mathrm{0},\mathrm{32}\right) \\ $$$$ \\ $$$$\frac{{x}_{{B}} −{x}_{{A}} }{{x}_{{A}} −{x}_{{O}'} }=\frac{{y}_{{B}} −{y}_{{A}} }{{y}_{{A}} −{y}_{{O}'} }=\frac{{z}_{{B}} −{z}_{{A}} }{{z}_{{A}} −{z}_{{O}'} } \\ $$$$\frac{{x}_{{B}} −\mathrm{4}}{\mathrm{4}−\mathrm{0}}=\frac{\mathrm{16}−\mathrm{13}}{\mathrm{13}−\mathrm{0}}=\frac{{z}_{{B}} −\mathrm{16}}{\mathrm{16}−\mathrm{32}} \\ $$$$\Rightarrow{x}_{{B}} =\mathrm{4}+\mathrm{4}×\frac{\mathrm{3}}{\mathrm{13}}=\frac{\mathrm{64}}{\mathrm{13}} \\ $$$$\Rightarrow{y}_{{B}} =\mathrm{16} \\ $$$$\Rightarrow{z}_{{B}} =\mathrm{16}−\mathrm{16}×\frac{\mathrm{3}}{\mathrm{13}}=\frac{\mathrm{160}}{\mathrm{13}} \\ $$$$ \\ $$$${A}'\left(\mathrm{4},\mathrm{19},\mathrm{16}\right) \\ $$$$\frac{{x}_{{C}} −{x}_{{B}} }{{x}_{{B}} −{x}_{{A}'} }=\frac{{y}_{{C}} −{y}_{{B}} }{{y}_{{B}} −{y}_{{A}'} }=\frac{{z}_{{C}} −{z}_{{B}} }{{z}_{{B}} −{z}_{{A}'} } \\ $$$$\frac{{x}_{{C}} −\frac{\mathrm{64}}{\mathrm{13}}}{\frac{\mathrm{64}}{\mathrm{13}}−\mathrm{4}}=\frac{{y}_{{C}} −\mathrm{16}}{\mathrm{16}−\mathrm{19}}=\frac{\mathrm{0}−\frac{\mathrm{160}}{\mathrm{13}}}{\frac{\mathrm{160}}{\mathrm{13}}−\mathrm{16}} \\ $$$$\Rightarrow{x}_{{C}} =\frac{\mathrm{64}}{\mathrm{13}}+\frac{\mathrm{12}}{\mathrm{13}}×\left(\frac{\mathrm{10}}{\mathrm{3}}\right)=\frac{\mathrm{104}}{\mathrm{13}}=\mathrm{8} \\ $$$$\Rightarrow{y}_{{C}} =\mathrm{16}−\mathrm{3}×\frac{\mathrm{10}}{\mathrm{3}}=\mathrm{6} \\ $$$$\Rightarrow{z}_{{C}} =\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow{B}\left(\frac{\mathrm{64}}{\mathrm{13}},\mathrm{16},\frac{\mathrm{160}}{\mathrm{13}}\right) \\ $$$$\Rightarrow{C}\left(\mathrm{8},\mathrm{6},\mathrm{0}\right) \\ $$
Commented by ajfour last updated on 22/Nov/17

$${thank}\:{you}\:{sir}\:! \\ $$
Commented by mrW1 last updated on 22/Nov/17

$${Related}\:{question}:\:{which}\:{point}\left({s}\right)\:{A} \\ $$$${on}\:{the}\:{roof}\:{plane}\:{can}\:{be}\:{selected} \\ $$$${such}\:{that}\:\boldsymbol{{C}}=\boldsymbol{{O}}? \\ $$
Commented by mrW1 last updated on 23/Nov/17
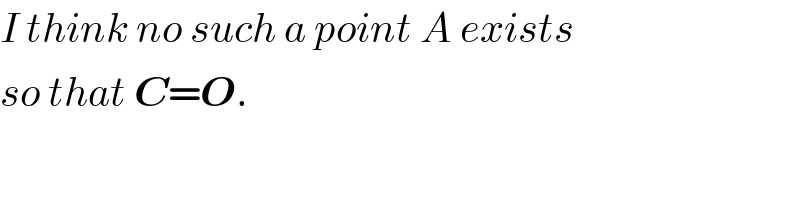
$${I}\:{think}\:{no}\:{such}\:{a}\:{point}\:{A}\:{exists} \\ $$$${so}\:{that}\:\boldsymbol{{C}}=\boldsymbol{{O}}. \\ $$
Commented by ajfour last updated on 22/Nov/17
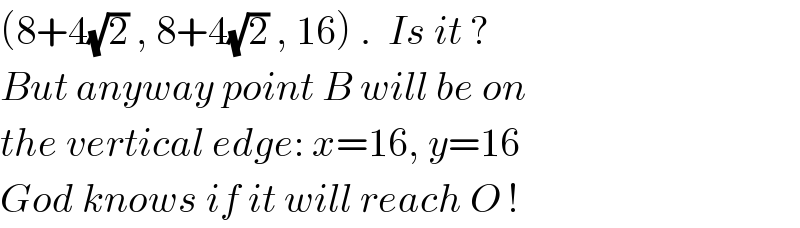
$$\left(\mathrm{8}+\mathrm{4}\sqrt{\mathrm{2}}\:,\:\mathrm{8}+\mathrm{4}\sqrt{\mathrm{2}}\:,\:\mathrm{16}\right)\:.\:\:{Is}\:{it}\:? \\ $$$${But}\:{anyway}\:{point}\:{B}\:{will}\:{be}\:{on} \\ $$$${the}\:{vertical}\:{edge}:\:{x}=\mathrm{16},\:{y}=\mathrm{16} \\ $$$${God}\:{knows}\:{if}\:{it}\:{will}\:{reach}\:{O}\:! \\ $$
