
Question Number 24555 by ajfour last updated on 20/Nov/17
Commented by ajfour last updated on 20/Nov/17

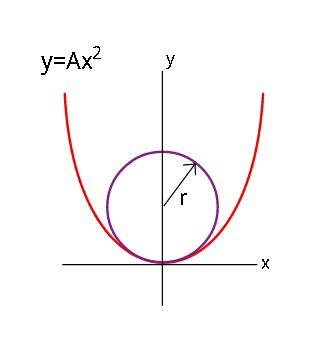
$${Find}\:{the}\:{maximum}\:{radius}\:{of} \\ $$$${a}\:{circle}\:{such}\:{that}\:{it}\:{touches}\:{the} \\ $$$${parabola}\:{y}={Ax}^{\mathrm{2}} \:{at}\:{its}\:{vertex}, \\ $$$${and}\:{lies}\:{above}\:{it}\:{and}\:{cuts}\:{it} \\ $$$${nowhere}. \\ $$
Commented by mrW1 last updated on 21/Nov/17
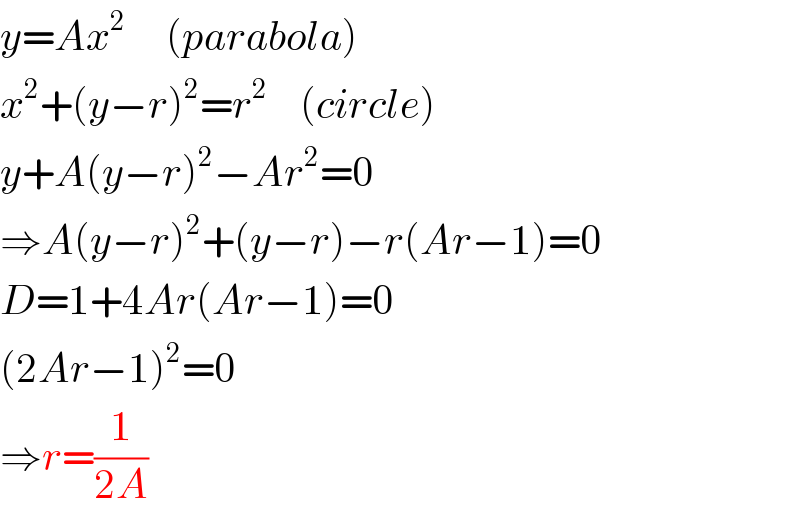
$${y}={Ax}^{\mathrm{2}} \:\:\:\:\:\left({parabola}\right) \\ $$$${x}^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \:\:\:\:\left({circle}\right) \\ $$$${y}+{A}\left({y}−{r}\right)^{\mathrm{2}} −{Ar}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{A}\left({y}−{r}\right)^{\mathrm{2}} +\left({y}−{r}\right)−{r}\left({Ar}−\mathrm{1}\right)=\mathrm{0} \\ $$$${D}=\mathrm{1}+\mathrm{4}{Ar}\left({Ar}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\left(\mathrm{2}{Ar}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{r}=\frac{\mathrm{1}}{\mathrm{2}{A}} \\ $$
Commented by ajfour last updated on 20/Nov/17

$${thank}\:{you}\:{sir}. \\ $$
Answered by ajfour last updated on 20/Nov/17
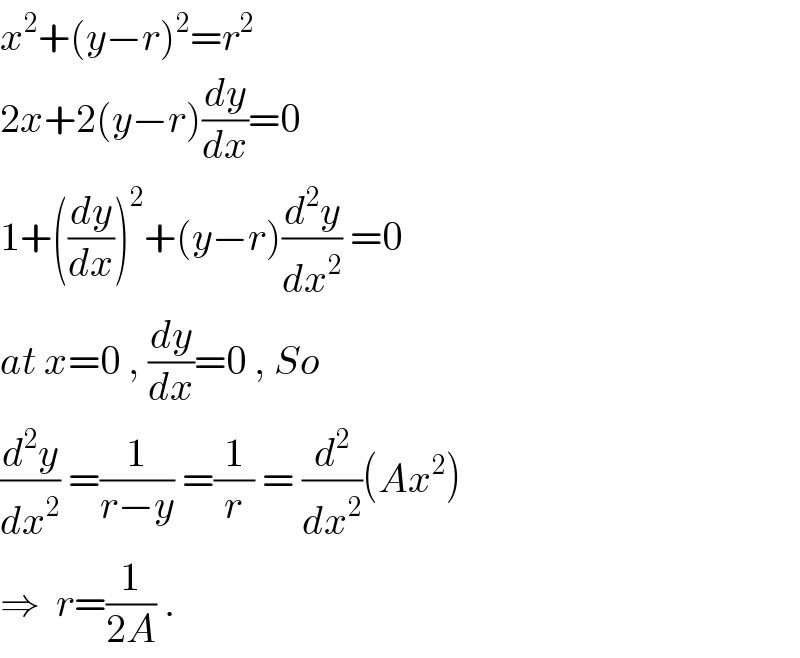
$${x}^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\mathrm{2}{x}+\mathrm{2}\left({y}−{r}\right)\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\mathrm{1}+\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} +\left({y}−{r}\right)\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\mathrm{0} \\ $$$${at}\:{x}=\mathrm{0}\:,\:\frac{{dy}}{{dx}}=\mathrm{0}\:,\:{So} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{{r}−{y}}\:=\frac{\mathrm{1}}{{r}}\:=\:\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left({Ax}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:{r}=\frac{\mathrm{1}}{\mathrm{2}{A}}\:. \\ $$
