
Question Number 24548 by Physics lover last updated on 20/Nov/17
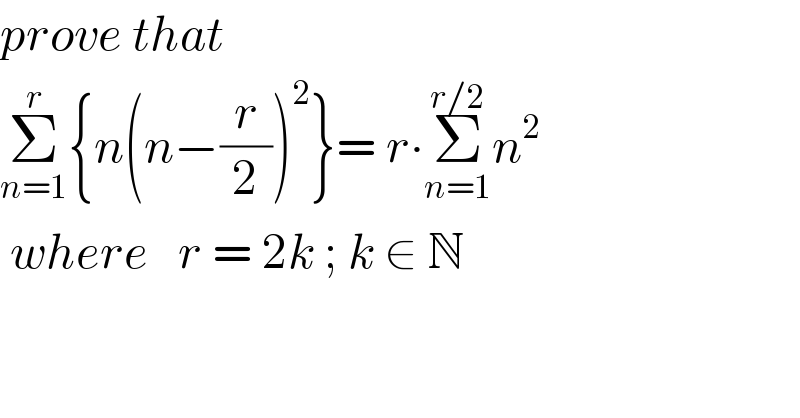
$${prove}\:{that}\: \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{r}} {\sum}}\left\{{n}\left({n}−\frac{{r}}{\mathrm{2}}\right)^{\mathrm{2}} \right\}=\:{r}\centerdot\underset{{n}=\mathrm{1}} {\overset{{r}/\mathrm{2}} {\sum}}{n}^{\mathrm{2}} \\ $$$$\:{where}\:\:\:{r}\:=\:\mathrm{2}{k}\:;\:{k}\:\in\:\mathbb{N} \\ $$
Answered by jota last updated on 21/Nov/17
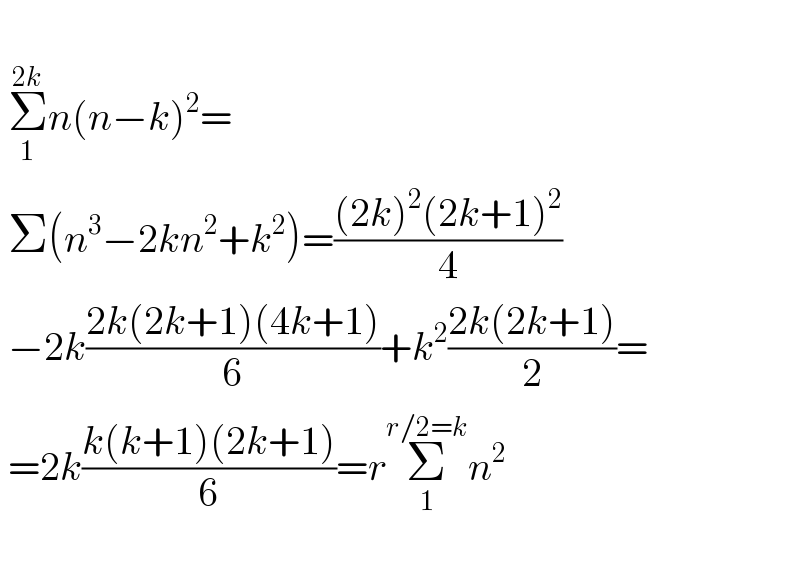
$$\: \\ $$$$\:\underset{\mathrm{1}} {\overset{\mathrm{2}{k}} {\sum}}{n}\left({n}−{k}\right)^{\mathrm{2}} = \\ $$$$\:\Sigma\left({n}^{\mathrm{3}} −\mathrm{2}{kn}^{\mathrm{2}} +{k}^{\mathrm{2}} \right)=\frac{\left(\mathrm{2}{k}\right)^{\mathrm{2}} \left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\:−\mathrm{2}{k}\frac{\mathrm{2}{k}\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{4}{k}+\mathrm{1}\right)}{\mathrm{6}}+{k}^{\mathrm{2}} \frac{\mathrm{2}{k}\left(\mathrm{2}{k}+\mathrm{1}\right)}{\mathrm{2}}= \\ $$$$\:=\mathrm{2}{k}\frac{{k}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}{\mathrm{6}}={r}\underset{\mathrm{1}} {\overset{{r}/\mathrm{2}={k}} {\sum}}{n}^{\mathrm{2}} \\ $$$$ \\ $$
Commented by Physics lover last updated on 21/Nov/17
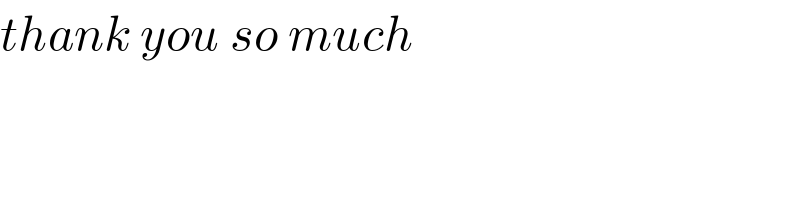
$${thank}\:{you}\:{so}\:{much} \\ $$
