Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 24520 by Tinkutara last updated on 19/Nov/17

A particle moves in a straight line along x-axis. At t = 0 it passes origin with some velocity towards positive x-axis and with an acceleration a which is given as, a = − Kx, where x is in metre and K is a positive constant. The time at which its velocity becomes half of its value at t = 0 for the first time, is

$$\mathrm{A}\:\mathrm{particle}\:\mathrm{moves}\:\mathrm{in}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}\:\mathrm{along} \\ $$$${x}-\mathrm{axis}.\:\mathrm{At}\:{t}\:=\:\mathrm{0}\:\mathrm{it}\:\mathrm{passes}\:\mathrm{origin}\:\mathrm{with} \\ $$$$\mathrm{some}\:\mathrm{velocity}\:\mathrm{towards}\:\mathrm{positive}\:{x}-\mathrm{axis} \\ $$$$\mathrm{and}\:\mathrm{with}\:\mathrm{an}\:\mathrm{acceleration}\:{a}\:\mathrm{which}\:\mathrm{is} \\ $$$$\mathrm{given}\:\mathrm{as},\:{a}\:=\:−\:{Kx},\:\mathrm{where}\:{x}\:\mathrm{is}\:\mathrm{in}\:\mathrm{metre} \\ $$$$\mathrm{and}\:{K}\:\mathrm{is}\:\mathrm{a}\:\mathrm{positive}\:\mathrm{constant}.\:\mathrm{The}\:\mathrm{time} \\ $$$$\mathrm{at}\:\mathrm{which}\:\mathrm{its}\:\mathrm{velocity}\:\mathrm{becomes}\:\mathrm{half}\:\mathrm{of}\:\mathrm{its} \\ $$$$\mathrm{value}\:\mathrm{at}\:{t}\:=\:\mathrm{0}\:\mathrm{for}\:\mathrm{the}\:\mathrm{first}\:\mathrm{time},\:\mathrm{is} \\ $$

Answered by mrW1 last updated on 19/Nov/17

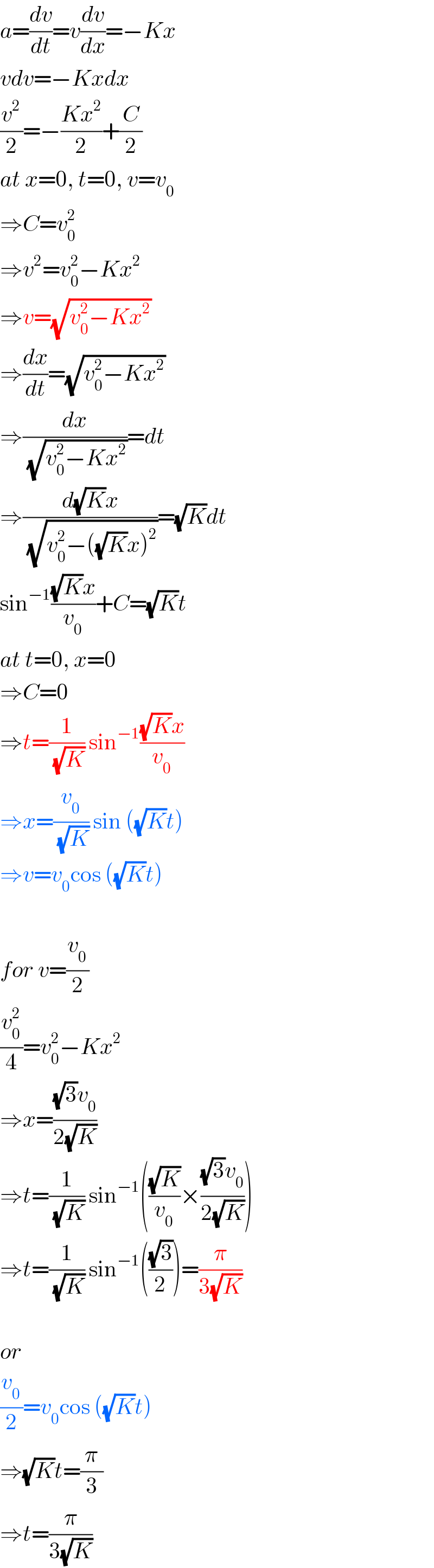
a=(dv/dt)=v(dv/dx)=−Kx vdv=−Kxdx (v^2 /2)=−((Kx^2 )/2)+(C/2) at x=0, t=0, v=v_0 ⇒C=v_0 ^2 ⇒v^2 =v_0 ^2 −Kx^2 ⇒v=(√(v_0 ^2 −Kx^2 )) ⇒(dx/dt)=(√(v_0 ^2 −Kx^2 )) ⇒(dx/(√(v_0 ^2 −Kx^2 )))=dt ⇒((d(√K)x)/(√(v_0 ^2 −((√K)x)^2 )))=(√K)dt sin^(−1) (((√K)x)/v_0 )+C=(√K)t at t=0, x=0 ⇒C=0 ⇒t=(1/(√K)) sin^(−1) (((√K)x)/v_0 ) ⇒x=(v_0 /(√K)) sin ((√K)t) ⇒v=v_0 cos ((√K)t) for v=(v_0 /2) (v_0 ^2 /4)=v_0 ^2 −Kx^2 ⇒x=(((√3)v_0 )/(2(√K))) ⇒t=(1/(√K)) sin^(−1) (((√K)/v_0 )×(((√3)v_0 )/(2(√K)))) ⇒t=(1/(√K)) sin^(−1) (((√3)/2))=(π/(3(√K))) or (v_0 /2)=v_0 cos ((√K)t) ⇒(√K)t=(π/3) ⇒t=(π/(3(√K)))

$${a}=\frac{{dv}}{{dt}}={v}\frac{{dv}}{{dx}}=−{Kx} \\ $$$${vdv}=−{Kxdx} \\ $$$$\frac{{v}^{\mathrm{2}} }{\mathrm{2}}=−\frac{{Kx}^{\mathrm{2}} }{\mathrm{2}}+\frac{{C}}{\mathrm{2}} \\ $$$${at}\:{x}=\mathrm{0},\:{t}=\mathrm{0},\:{v}={v}_{\mathrm{0}} \\ $$$$\Rightarrow{C}={v}_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$\Rightarrow{v}^{\mathrm{2}} ={v}_{\mathrm{0}} ^{\mathrm{2}} −{Kx}^{\mathrm{2}} \\ $$$$\Rightarrow{v}=\sqrt{{v}_{\mathrm{0}} ^{\mathrm{2}} −{Kx}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{dx}}{{dt}}=\sqrt{{v}_{\mathrm{0}} ^{\mathrm{2}} −{Kx}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{dx}}{\sqrt{{v}_{\mathrm{0}} ^{\mathrm{2}} −{Kx}^{\mathrm{2}} }}={dt} \\ $$$$\Rightarrow\frac{{d}\sqrt{{K}}{x}}{\sqrt{{v}_{\mathrm{0}} ^{\mathrm{2}} −\left(\sqrt{{K}}{x}\right)^{\mathrm{2}} }}=\sqrt{{K}}{dt} \\ $$$$\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{{K}}{x}}{{v}_{\mathrm{0}} }+{C}=\sqrt{{K}}{t} \\ $$$${at}\:{t}=\mathrm{0},\:{x}=\mathrm{0} \\ $$$$\Rightarrow{C}=\mathrm{0} \\ $$$$\Rightarrow{t}=\frac{\mathrm{1}}{\sqrt{{K}}}\:\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{{K}}{x}}{{v}_{\mathrm{0}} } \\ $$$$\Rightarrow{x}=\frac{{v}_{\mathrm{0}} }{\sqrt{{K}}}\:\mathrm{sin}\:\left(\sqrt{{K}}{t}\right) \\ $$$$\Rightarrow{v}={v}_{\mathrm{0}} \mathrm{cos}\:\left(\sqrt{{K}}{t}\right) \\ $$$$ \\ $$$${for}\:{v}=\frac{{v}_{\mathrm{0}} }{\mathrm{2}} \\ $$$$\frac{{v}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{4}}={v}_{\mathrm{0}} ^{\mathrm{2}} −{Kx}^{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\sqrt{\mathrm{3}}{v}_{\mathrm{0}} }{\mathrm{2}\sqrt{{K}}} \\ $$$$\Rightarrow{t}=\frac{\mathrm{1}}{\sqrt{{K}}}\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\sqrt{{K}}}{{v}_{\mathrm{0}} }×\frac{\sqrt{\mathrm{3}}{v}_{\mathrm{0}} }{\mathrm{2}\sqrt{{K}}}\right) \\ $$$$\Rightarrow{t}=\frac{\mathrm{1}}{\sqrt{{K}}}\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=\frac{\pi}{\mathrm{3}\sqrt{{K}}} \\ $$$$ \\ $$$${or} \\ $$$$\frac{{v}_{\mathrm{0}} }{\mathrm{2}}={v}_{\mathrm{0}} \mathrm{cos}\:\left(\sqrt{{K}}{t}\right) \\ $$$$\Rightarrow\sqrt{{K}}{t}=\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow{t}=\frac{\pi}{\mathrm{3}\sqrt{{K}}} \\ $$

Commented by Tinkutara last updated on 20/Nov/17

Thank you very much Sir! That′s I want because I had not studied SHM.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$$$\mathrm{That}'\mathrm{s}\:\mathrm{I}\:\mathrm{want}\:\mathrm{because}\:\mathrm{I}\:\mathrm{had}\:\mathrm{not} \\ $$$$\mathrm{studied}\:\mathrm{SHM}. \\ $$

Answered by ajfour last updated on 20/Nov/17

a=−ω^2 x for S.H.M. along x. lets take x=Asin (ωt+φ) as x=0 at t=0 ⇒ φ = 0, π v=ωAcos (ωt+φ) as v>0 at t=0 ⇒ φ=0 and ≠π so x=Asin 𝛚t and v=ωAcos ωt v_0 =ωA so (v_0 /2)=((ωA)/2) v_1 = ((ωA)/2) =ωAcos ωt_1 ⇒ cos ωt_1 =(1/2) or t_1 =(π/(3ω)) = (π/(3(√K))) .

$${a}=−\omega^{\mathrm{2}} {x}\:\:\:{for}\:\:{S}.{H}.{M}.\:{along}\:{x}. \\ $$$${lets}\:{take}\:\:\:\:\:\:{x}={A}\mathrm{sin}\:\left(\omega{t}+\phi\right) \\ $$$${as}\:{x}=\mathrm{0}\:\:{at}\:\:{t}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\phi\:=\:\mathrm{0},\:\pi \\ $$$${v}=\omega{A}\mathrm{cos}\:\left(\omega{t}+\phi\right) \\ $$$${as}\:{v}>\mathrm{0}\:{at}\:{t}=\mathrm{0}\:\:\:\Rightarrow\:\:\:\phi=\mathrm{0}\:{and}\:\neq\pi \\ $$$${so}\:\:\:\:\:\boldsymbol{{x}}=\boldsymbol{{A}}\mathrm{sin}\:\boldsymbol{\omega{t}} \\ $$$${and}\:{v}=\omega{A}\mathrm{cos}\:\omega{t} \\ $$$${v}_{\mathrm{0}} =\omega{A}\:\:\:\:\:{so}\:\:\frac{{v}_{\mathrm{0}} }{\mathrm{2}}=\frac{\omega{A}}{\mathrm{2}} \\ $$$$\:\:\:{v}_{\mathrm{1}} =\:\frac{\omega{A}}{\mathrm{2}}\:=\omega{A}\mathrm{cos}\:\omega{t}_{\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{cos}\:\omega{t}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${or}\:\:\:{t}_{\mathrm{1}} =\frac{\pi}{\mathrm{3}\omega}\:=\:\frac{\pi}{\mathrm{3}\sqrt{{K}}}\:. \\ $$

Commented by Tinkutara last updated on 20/Nov/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Commented by Tinkutara last updated on 20/Nov/17

Using SHM, I will need it later.

$$\mathrm{Using}\:\mathrm{SHM},\:\mathrm{I}\:\mathrm{will}\:\mathrm{need}\:\mathrm{it}\:\mathrm{later}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com