
Question Number 24482 by Tinkutara last updated on 18/Nov/17

$$\mathrm{Neglecting}\:\mathrm{friction}\:\mathrm{and}\:\mathrm{mass}\:\mathrm{of}\:\mathrm{pulleys}, \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{acceleration}\:\mathrm{of}\:\mathrm{mass}\:{B}? \\ $$
Commented by ajfour last updated on 18/Nov/17
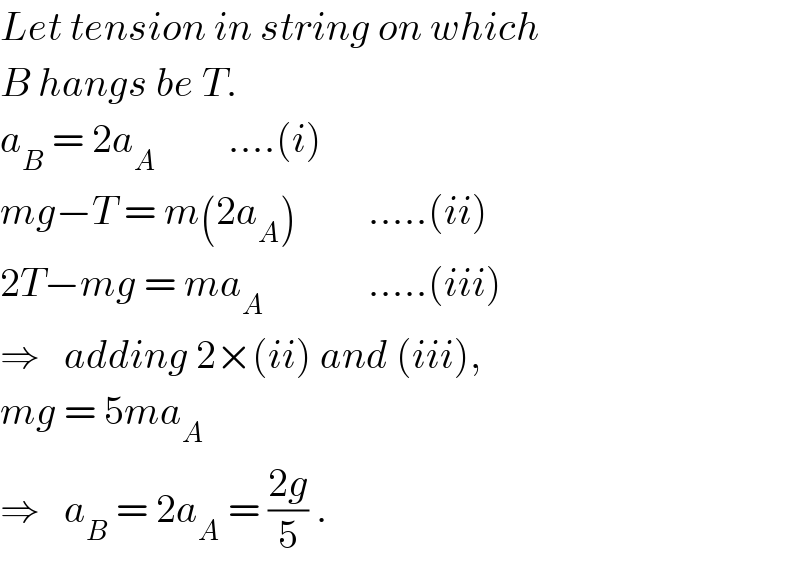
$${Let}\:{tension}\:{in}\:{string}\:{on}\:{which} \\ $$$${B}\:{hangs}\:{be}\:{T}. \\ $$$${a}_{{B}} \:=\:\mathrm{2}{a}_{{A}} \:\:\:\:\:\:\:\:\:....\left({i}\right) \\ $$$${mg}−{T}\:=\:{m}\left(\mathrm{2}{a}_{{A}} \right)\:\:\:\:\:\:\:\:\:.....\left({ii}\right) \\ $$$$\mathrm{2}{T}−{mg}\:=\:{ma}_{{A}} \:\:\:\:\:\:\:\:\:\:\:\:\:.....\left({iii}\right) \\ $$$$\Rightarrow\:\:\:{adding}\:\mathrm{2}×\left({ii}\right)\:{and}\:\left({iii}\right), \\ $$$${mg}\:=\:\mathrm{5}{ma}_{{A}} \\ $$$$\Rightarrow\:\:\:{a}_{{B}} \:=\:\mathrm{2}{a}_{{A}} \:=\:\frac{\mathrm{2}{g}}{\mathrm{5}}\:. \\ $$
Commented by Tinkutara last updated on 18/Nov/17
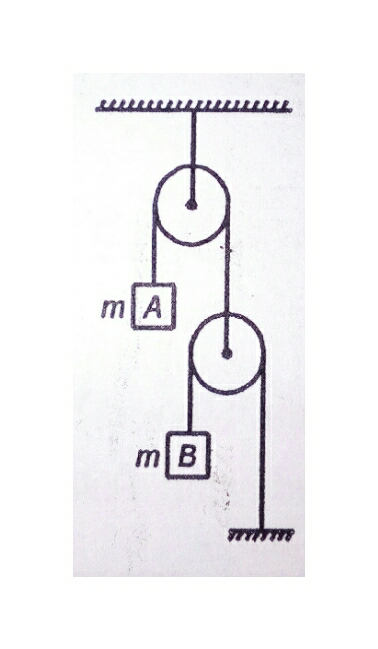
Commented by mrW1 last updated on 18/Nov/17
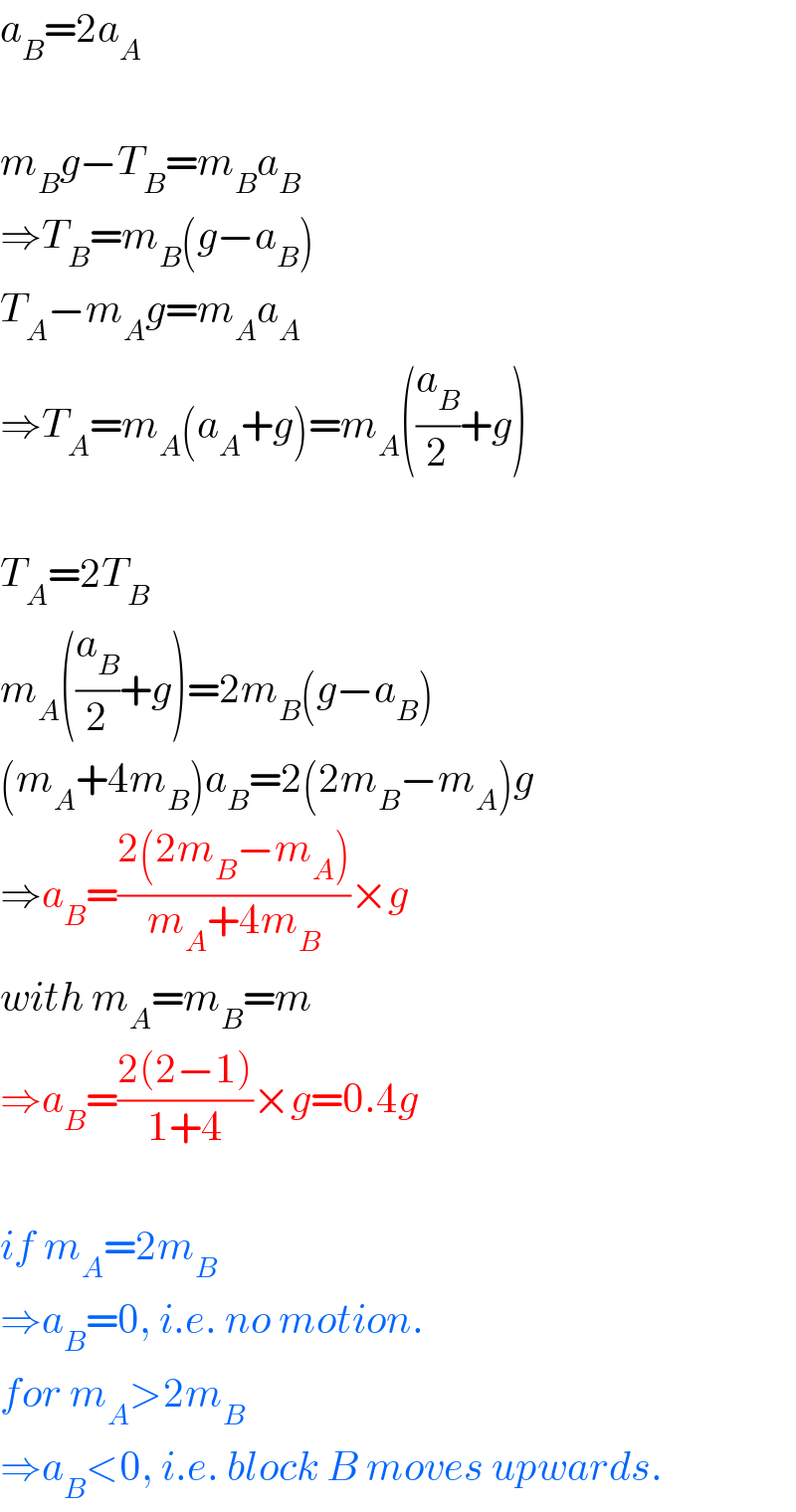
$${a}_{{B}} =\mathrm{2}{a}_{{A}} \\ $$$$ \\ $$$${m}_{{B}} {g}−{T}_{{B}} ={m}_{{B}} {a}_{{B}} \\ $$$$\Rightarrow{T}_{{B}} ={m}_{{B}} \left({g}−{a}_{{B}} \right) \\ $$$${T}_{{A}} −{m}_{{A}} {g}={m}_{{A}} {a}_{{A}} \\ $$$$\Rightarrow{T}_{{A}} ={m}_{{A}} \left({a}_{{A}} +{g}\right)={m}_{{A}} \left(\frac{{a}_{{B}} }{\mathrm{2}}+{g}\right) \\ $$$$ \\ $$$${T}_{{A}} =\mathrm{2}{T}_{{B}} \\ $$$${m}_{{A}} \left(\frac{{a}_{{B}} }{\mathrm{2}}+{g}\right)=\mathrm{2}{m}_{{B}} \left({g}−{a}_{{B}} \right) \\ $$$$\left({m}_{{A}} +\mathrm{4}{m}_{{B}} \right){a}_{{B}} =\mathrm{2}\left(\mathrm{2}{m}_{{B}} −{m}_{{A}} \right){g} \\ $$$$\Rightarrow{a}_{{B}} =\frac{\mathrm{2}\left(\mathrm{2}{m}_{{B}} −{m}_{{A}} \right)}{{m}_{{A}} +\mathrm{4}{m}_{{B}} }×{g} \\ $$$${with}\:{m}_{{A}} ={m}_{{B}} ={m} \\ $$$$\Rightarrow{a}_{{B}} =\frac{\mathrm{2}\left(\mathrm{2}−\mathrm{1}\right)}{\mathrm{1}+\mathrm{4}}×{g}=\mathrm{0}.\mathrm{4}{g} \\ $$$$ \\ $$$${if}\:{m}_{{A}} =\mathrm{2}{m}_{{B}} \\ $$$$\Rightarrow{a}_{{B}} =\mathrm{0},\:{i}.{e}.\:{no}\:{motion}. \\ $$$${for}\:{m}_{{A}} >\mathrm{2}{m}_{{B}} \\ $$$$\Rightarrow{a}_{{B}} <\mathrm{0},\:{i}.{e}.\:{block}\:{B}\:{moves}\:{upwards}. \\ $$
Commented by Tinkutara last updated on 19/Nov/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sirs}! \\ $$
