
Question Number 23700 by Tinkutara last updated on 04/Nov/17
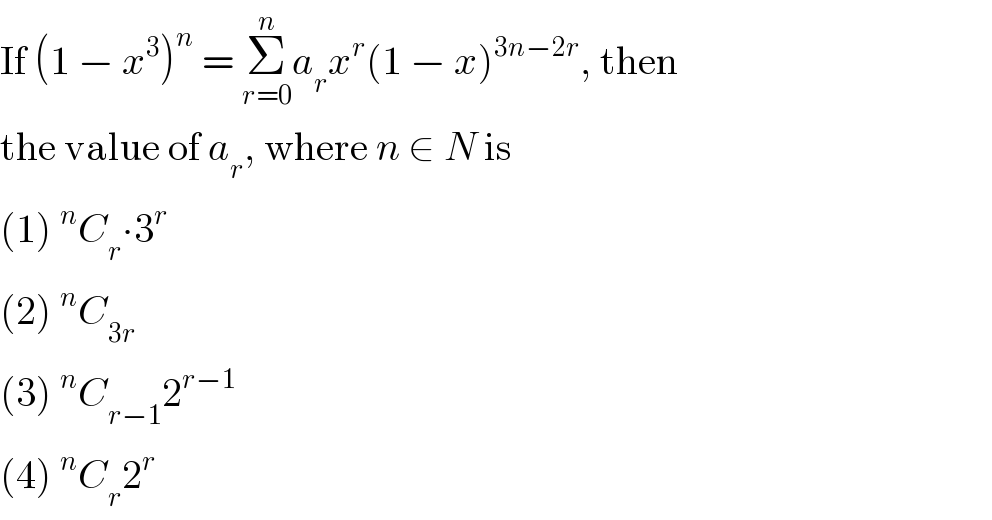
$$\mathrm{If}\:\left(\mathrm{1}\:−\:{x}^{\mathrm{3}} \right)^{{n}} \:=\:\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{r}} {x}^{{r}} \left(\mathrm{1}\:−\:{x}\right)^{\mathrm{3}{n}−\mathrm{2}{r}} ,\:\mathrm{then} \\ $$$$\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{a}_{{r}} ,\:\mathrm{where}\:{n}\:\in\:{N}\:\mathrm{is} \\ $$$$\left(\mathrm{1}\right)\:^{{n}} {C}_{{r}} \centerdot\mathrm{3}^{{r}} \\ $$$$\left(\mathrm{2}\right)\:^{{n}} {C}_{\mathrm{3}{r}} \\ $$$$\left(\mathrm{3}\right)\:^{{n}} {C}_{{r}−\mathrm{1}} \mathrm{2}^{{r}−\mathrm{1}} \\ $$$$\left(\mathrm{4}\right)\:^{{n}} {C}_{{r}} \mathrm{2}^{{r}} \\ $$
Commented by ajfour last updated on 04/Nov/17

$${If}\:{n}=\mathrm{1} \\ $$$$\mathrm{1}−{x}^{\mathrm{3}} ={a}_{\mathrm{0}} \left(\mathrm{1}−{x}\right)^{\mathrm{3}} +{a}_{\mathrm{1}} {x}\left(\mathrm{1}−{x}\right) \\ $$$$\Rightarrow\:{a}_{\mathrm{0}} =\mathrm{1}\:\:{and}\:\:{a}_{\mathrm{1}} =\mathrm{3} \\ $$$${if}\:{we}\:{check}\:{options}\:{with}\:{n}=\mathrm{1} \\ $$$$\left(\mathrm{1}\right)\:{gives}\:{a}_{\mathrm{0}} =\mathrm{1},\:{a}_{\mathrm{1}} =\mathrm{3} \\ $$$$\left(\mathrm{2}\right)\:{a}_{\mathrm{0}} =\mathrm{1},\:{a}_{\mathrm{1}} =! \\ $$$$\left(\mathrm{3}\right)\:{a}_{\mathrm{0}} =!\:,\:{a}_{\mathrm{1}} =\mathrm{1} \\ $$$$\left(\mathrm{4}\right)\:{a}_{\mathrm{0}} =\mathrm{1}\:,\:{a}_{\mathrm{1}} =\mathrm{2} \\ $$$${So}\:{only}\:{option}\:\left(\mathrm{1}\right)\:{qualifies}.. \\ $$
Commented by Tinkutara last updated on 05/Nov/17

$$\mathrm{Not}\:\mathrm{any}\:\mathrm{proof}? \\ $$
Commented by ajfour last updated on 05/Nov/17

$${i}\:{will}\:{try}\:.. \\ $$
