Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 175457 by Rasheed.Sindhi last updated on 30/Aug/22

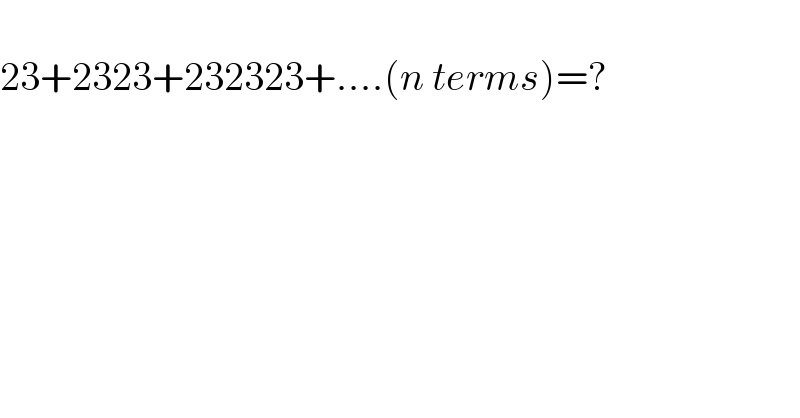
23+2323+232323+....(n terms)=?

$$ \\ $$$$\mathrm{23}+\mathrm{2323}+\mathrm{232323}+....\left({n}\:{terms}\right)=? \\ $$$$ \\ $$

Answered by Rasheed.Sindhi last updated on 01/Sep/22

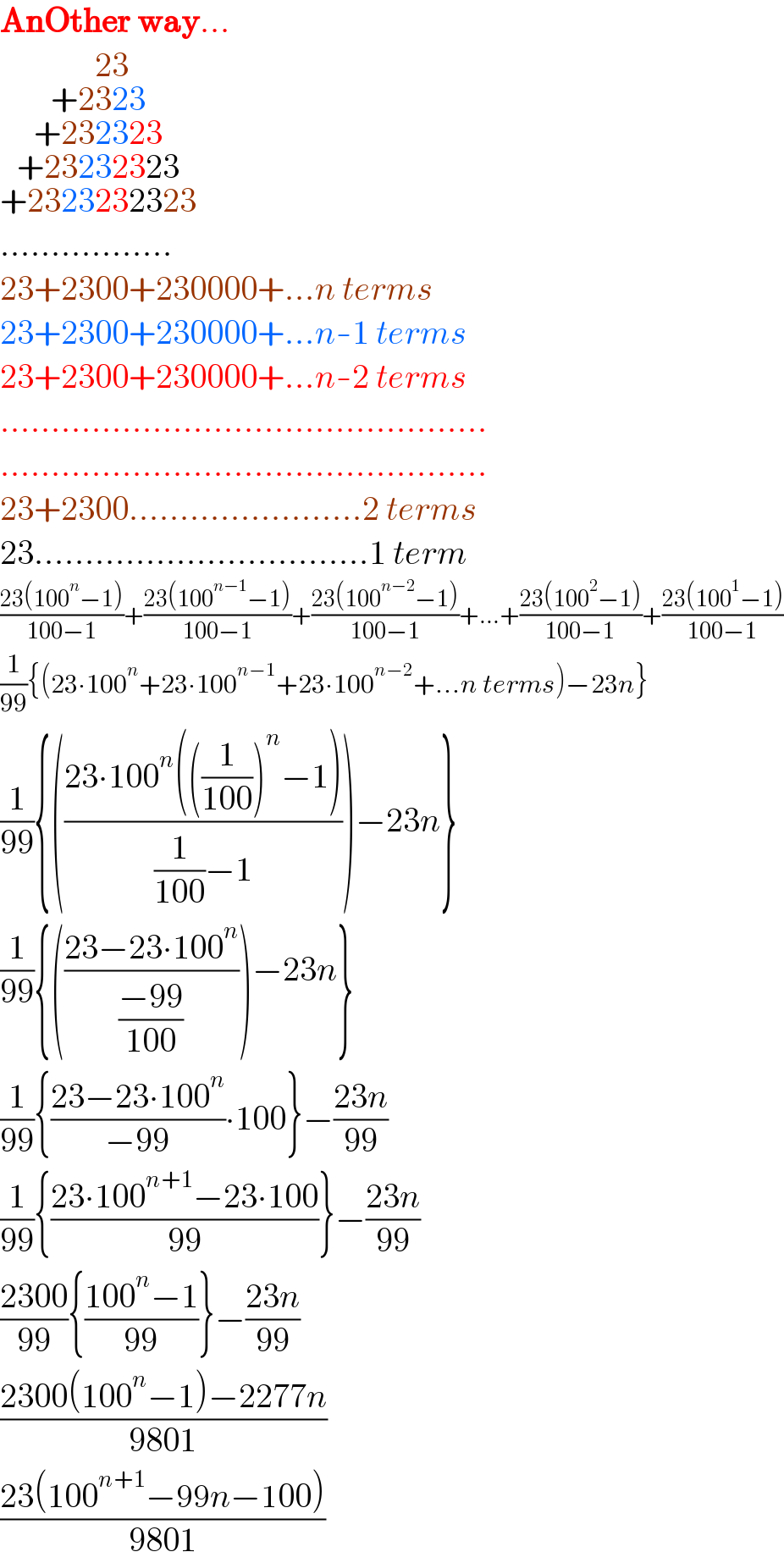
AnOther way... 23_(+2323_(+232323_(+23232323_(+2323232323) ) ) ) ................. 23+2300+230000+...n terms 23+2300+230000+...n-1 terms 23+2300+230000+...n-2 terms ................................................ ................................................ 23+2300.......................2 terms 23.................................1 term ((23(100^n −1))/(100−1))+((23(100^(n−1) −1))/(100−1))+((23(100^(n−2) −1))/(100−1))+...+((23(100^2 −1))/(100−1))+((23(100^1 −1))/(100−1)) (1/(99)){(23∙100^n +23∙100^(n−1) +23∙100^(n−2) +...n terms)−23n} (1/(99)){(((23∙100^n (((1/(100)))^n −1))/((1/(100))−1)))−23n} (1/(99)){(((23−23∙100^n )/((−99)/(100))))−23n} (1/(99)){((23−23∙100^n )/(−99))∙100}−((23n)/(99)) (1/(99)){((23∙100^(n+1) −23∙100)/(99))}−((23n)/(99)) ((2300)/(99)){((100^n −1)/(99))}−((23n)/(99)) ((2300(100^n −1)−2277n)/(9801)) ((23(100^(n+1) −99n−100))/(9801))

$$\boldsymbol{\mathrm{AnOther}}\:\boldsymbol{\mathrm{way}}... \\ $$$$\underset{\underset{\underset{\underset{+\mathrm{2323232323}} {+\mathrm{23232323}}} {+\mathrm{232323}}} {+\mathrm{2323}}} {\:\:\:\:\mathrm{23}} \\ $$$$................. \\ $$$$\mathrm{23}+\mathrm{2300}+\mathrm{230000}+...{n}\:{terms} \\ $$$$\mathrm{23}+\mathrm{2300}+\mathrm{230000}+...{n}-\mathrm{1}\:{terms} \\ $$$$\mathrm{23}+\mathrm{2300}+\mathrm{230000}+...{n}-\mathrm{2}\:{terms} \\ $$$$................................................ \\ $$$$................................................ \\ $$$$\mathrm{23}+\mathrm{2300}.......................\mathrm{2}\:{terms} \\ $$$$\mathrm{23}.................................\mathrm{1}\:{term} \\ $$$$\frac{\mathrm{23}\left(\mathrm{100}^{{n}} −\mathrm{1}\right)}{\mathrm{100}−\mathrm{1}}+\frac{\mathrm{23}\left(\mathrm{100}^{{n}−\mathrm{1}} −\mathrm{1}\right)}{\mathrm{100}−\mathrm{1}}+\frac{\mathrm{23}\left(\mathrm{100}^{{n}−\mathrm{2}} −\mathrm{1}\right)}{\mathrm{100}−\mathrm{1}}+...+\frac{\mathrm{23}\left(\mathrm{100}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{100}−\mathrm{1}}+\frac{\mathrm{23}\left(\mathrm{100}^{\mathrm{1}} −\mathrm{1}\right)}{\mathrm{100}−\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{99}}\left\{\left(\mathrm{23}\centerdot\mathrm{100}^{{n}} +\mathrm{23}\centerdot\mathrm{100}^{{n}−\mathrm{1}} +\mathrm{23}\centerdot\mathrm{100}^{{n}−\mathrm{2}} +...{n}\:{terms}\right)−\mathrm{23}{n}\right\} \\ $$$$\frac{\mathrm{1}}{\mathrm{99}}\left\{\left(\frac{\mathrm{23}\centerdot\mathrm{100}^{{n}} \left(\left(\frac{\mathrm{1}}{\mathrm{100}}\right)^{{n}} −\mathrm{1}\right)}{\frac{\mathrm{1}}{\mathrm{100}}−\mathrm{1}}\right)−\mathrm{23}{n}\right\} \\ $$$$\frac{\mathrm{1}}{\mathrm{99}}\left\{\left(\frac{\mathrm{23}−\mathrm{23}\centerdot\mathrm{100}^{{n}} }{\frac{−\mathrm{99}}{\mathrm{100}}}\right)−\mathrm{23}{n}\right\} \\ $$$$\frac{\mathrm{1}}{\mathrm{99}}\left\{\frac{\mathrm{23}−\mathrm{23}\centerdot\mathrm{100}^{{n}} }{−\mathrm{99}}\centerdot\mathrm{100}\right\}−\frac{\mathrm{23}{n}}{\mathrm{99}} \\ $$$$\frac{\mathrm{1}}{\mathrm{99}}\left\{\frac{\mathrm{23}\centerdot\mathrm{100}^{{n}+\mathrm{1}} −\mathrm{23}\centerdot\mathrm{100}}{\mathrm{99}}\right\}−\frac{\mathrm{23}{n}}{\mathrm{99}} \\ $$$$\frac{\mathrm{2300}}{\mathrm{99}}\left\{\frac{\mathrm{100}^{{n}} −\mathrm{1}}{\mathrm{99}}\right\}−\frac{\mathrm{23}{n}}{\mathrm{99}} \\ $$$$\frac{\mathrm{2300}\left(\mathrm{100}^{{n}} −\mathrm{1}\right)−\mathrm{2277}{n}}{\mathrm{9801}} \\ $$$$\frac{\mathrm{23}\left(\mathrm{100}^{{n}+\mathrm{1}} −\mathrm{99}{n}−\mathrm{100}\right)}{\mathrm{9801}} \\ $$

Commented by infinityaction last updated on 01/Sep/22

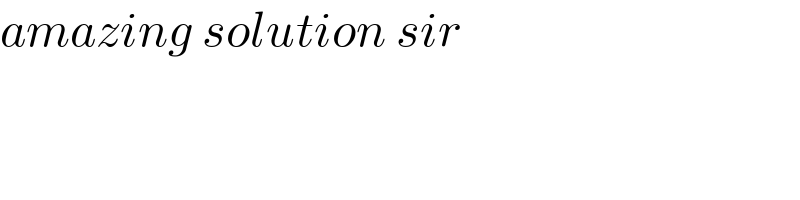
amazing solution sir

$${amazing}\:{solution}\:{sir} \\ $$

Commented by Rasheed.Sindhi last updated on 01/Sep/22

Thanks sir!

$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{sir}}! \\ $$

Commented by Tawa11 last updated on 15/Sep/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Commented by Rasheed.Sindhi last updated on 15/Sep/22

T^(H^A N) X_(MISS!)

$$\underset{\mathcal{MISS}!} {\mathbb{T}^{\mathbb{H}^{\mathbb{A}} \mathbb{N}} \mathbb{X}} \\ $$

Answered by Ar Brandon last updated on 30/Aug/22

Σu_n =23+2323+232323+23232323+... Δu_n =2300+230000+23000000+..., r=100 ⇒u_n =a×100^(n−1) +a_0 u_1 =23=a+a_0 u_2 =2323=100a+a_0 ⇒ { ((a+a_0 =23)),((100a+a_0 =2323)) :} ⇒a=((2300)/(99)), a_0 =23−((2300)/(99))=−((23)/(99)) ⇒u_n =((2300)/(99))×100^(n−1) −((23)/(99))=((23)/(99))(100^n −1) ⇒Σu_n =((2300)/(99))(((100^n −1)/(99)))−((23n)/(99)) =((23.100^(n+1) −2277n−2300)/(9801))

$$\Sigma{u}_{{n}} =\mathrm{23}+\mathrm{2323}+\mathrm{232323}+\mathrm{23232323}+... \\ $$$$\Delta{u}_{{n}} =\mathrm{2300}+\mathrm{230000}+\mathrm{23000000}+...,\:{r}=\mathrm{100} \\ $$$$\Rightarrow{u}_{{n}} ={a}×\mathrm{100}^{{n}−\mathrm{1}} +{a}_{\mathrm{0}} \\ $$$${u}_{\mathrm{1}} =\mathrm{23}={a}+{a}_{\mathrm{0}} \\ $$$${u}_{\mathrm{2}} =\mathrm{2323}=\mathrm{100}{a}+{a}_{\mathrm{0}} \:\Rightarrow\begin{cases}{{a}+{a}_{\mathrm{0}} =\mathrm{23}}\\{\mathrm{100}{a}+{a}_{\mathrm{0}} =\mathrm{2323}}\end{cases} \\ $$$$\Rightarrow{a}=\frac{\mathrm{2300}}{\mathrm{99}},\:{a}_{\mathrm{0}} =\mathrm{23}−\frac{\mathrm{2300}}{\mathrm{99}}=−\frac{\mathrm{23}}{\mathrm{99}} \\ $$$$\Rightarrow{u}_{{n}} =\frac{\mathrm{2300}}{\mathrm{99}}×\mathrm{100}^{{n}−\mathrm{1}} −\frac{\mathrm{23}}{\mathrm{99}}=\frac{\mathrm{23}}{\mathrm{99}}\left(\mathrm{100}^{{n}} −\mathrm{1}\right) \\ $$$$\Rightarrow\Sigma{u}_{{n}} =\frac{\mathrm{2300}}{\mathrm{99}}\left(\frac{\mathrm{100}^{{n}} −\mathrm{1}}{\mathrm{99}}\right)−\frac{\mathrm{23}{n}}{\mathrm{99}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{23}.\mathrm{100}^{{n}+\mathrm{1}} −\mathrm{2277}{n}−\mathrm{2300}}{\mathrm{9801}} \\ $$

Commented by Rasheed.Sindhi last updated on 01/Sep/22

Thanks sir!

$$\mathbb{T}\mathrm{han}\Bbbk\mathrm{s}\:\mathrm{sir}! \\ $$

Answered by Rasheed.Sindhi last updated on 31/Aug/22

S_n =23+2323+232323+....(n terms) (S_n /(23))=1+101+10101+1010101+...(n terms) ((99S_n )/(23))=99+9999+999999+99999999+...(n terms) =(100−1)+(10000−1)+(1000000−1)+...(n terms) =(10^2 +10^4 +10^6 +...(n terms))−n =((10^2 (10^(2n) −1))/(10^2 −1))−n =((10^(2n+2) −99n−10^2 )/(99)) S_n =((23(10^(2n+2) −99n−100))/(99×99)) =((23(10^(2n+2) −99n−100))/(9801))

$${S}_{{n}} =\mathrm{23}+\mathrm{2323}+\mathrm{232323}+....\left({n}\:{terms}\right) \\ $$$$\frac{{S}_{{n}} }{\mathrm{23}}=\mathrm{1}+\mathrm{101}+\mathrm{10101}+\mathrm{1010101}+...\left({n}\:{terms}\right) \\ $$$$\frac{\mathrm{99}{S}_{{n}} }{\mathrm{23}}=\mathrm{99}+\mathrm{9999}+\mathrm{999999}+\mathrm{99999999}+...\left({n}\:{terms}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{100}−\mathrm{1}\right)+\left(\mathrm{10000}−\mathrm{1}\right)+\left(\mathrm{1000000}−\mathrm{1}\right)+...\left({n}\:{terms}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\left(\mathrm{10}^{\mathrm{2}} +\mathrm{10}^{\mathrm{4}} +\mathrm{10}^{\mathrm{6}} +...\left({n}\:{terms}\right)\right)−{n} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{10}^{\mathrm{2}} \left(\mathrm{10}^{\mathrm{2}{n}} −\mathrm{1}\right)}{\mathrm{10}^{\mathrm{2}} −\mathrm{1}}−{n} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{10}^{\mathrm{2}{n}+\mathrm{2}} −\mathrm{99}{n}−\mathrm{10}^{\mathrm{2}} }{\mathrm{99}} \\ $$$${S}_{{n}} =\frac{\mathrm{23}\left(\mathrm{10}^{\mathrm{2}{n}+\mathrm{2}} −\mathrm{99}{n}−\mathrm{100}\right)}{\mathrm{99}×\mathrm{99}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{23}\left(\mathrm{10}^{\mathrm{2}{n}+\mathrm{2}} −\mathrm{99}{n}−\mathrm{100}\right)}{\mathrm{9801}} \\ $$

Commented by peter frank last updated on 31/Aug/22

thanks

$$\mathrm{thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com