
Question Number 22872 by Physics lover last updated on 23/Oct/17
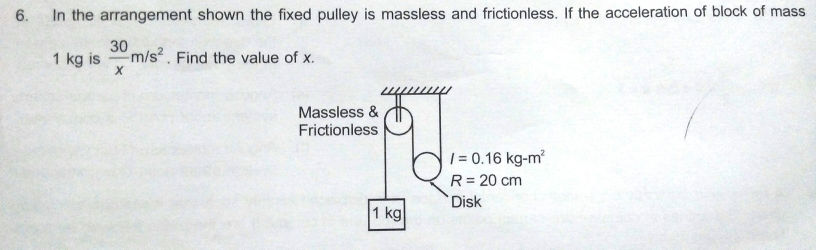
Commented by ajfour last updated on 23/Oct/17

Commented by ajfour last updated on 24/Oct/17
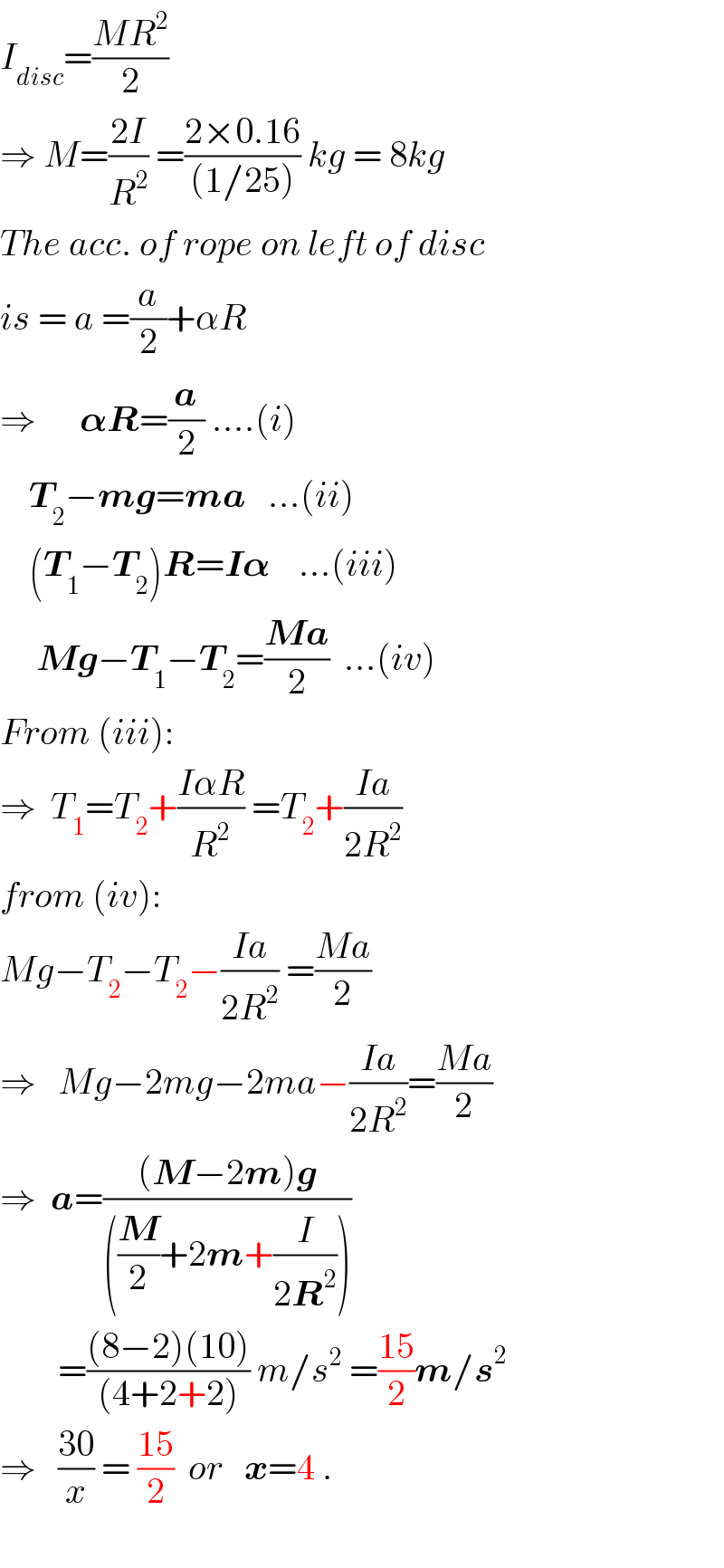
$${I}_{{disc}} =\frac{{MR}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\:{M}=\frac{\mathrm{2}{I}}{{R}^{\mathrm{2}} }\:=\frac{\mathrm{2}×\mathrm{0}.\mathrm{16}}{\left(\mathrm{1}/\mathrm{25}\right)}\:{kg}\:=\:\mathrm{8}{kg} \\ $$$${The}\:{acc}.\:{of}\:{rope}\:{on}\:{left}\:{of}\:{disc} \\ $$$${is}\:=\:{a}\:=\frac{{a}}{\mathrm{2}}+\alpha{R} \\ $$$$\Rightarrow\:\:\:\:\:\:\boldsymbol{\alpha{R}}=\frac{\boldsymbol{{a}}}{\mathrm{2}}\:....\left({i}\right) \\ $$$$\:\:\:\:\boldsymbol{{T}}_{\mathrm{2}} −\boldsymbol{{mg}}=\boldsymbol{{ma}}\:\:\:...\left({ii}\right) \\ $$$$\:\:\:\:\left(\boldsymbol{{T}}_{\mathrm{1}} −\boldsymbol{{T}}_{\mathrm{2}} \right)\boldsymbol{{R}}=\boldsymbol{{I}\alpha}\:\:\:\:...\left({iii}\right) \\ $$$$\:\:\:\:\:\boldsymbol{{Mg}}−\boldsymbol{{T}}_{\mathrm{1}} −\boldsymbol{{T}}_{\mathrm{2}} =\frac{\boldsymbol{{Ma}}}{\mathrm{2}}\:\:...\left({iv}\right) \\ $$$${From}\:\left({iii}\right): \\ $$$$\Rightarrow\:\:{T}_{\mathrm{1}} ={T}_{\mathrm{2}} +\frac{{I}\alpha{R}}{{R}^{\mathrm{2}} }\:={T}_{\mathrm{2}} +\frac{{Ia}}{\mathrm{2}{R}^{\mathrm{2}} } \\ $$$${from}\:\left({iv}\right): \\ $$$${Mg}−{T}_{\mathrm{2}} −{T}_{\mathrm{2}} −\frac{{Ia}}{\mathrm{2}{R}^{\mathrm{2}} }\:=\frac{{Ma}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:{Mg}−\mathrm{2}{mg}−\mathrm{2}{ma}−\frac{{Ia}}{\mathrm{2}{R}^{\mathrm{2}} }=\frac{{Ma}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\boldsymbol{{a}}=\frac{\left(\boldsymbol{{M}}−\mathrm{2}\boldsymbol{{m}}\right)\boldsymbol{{g}}}{\left(\frac{\boldsymbol{{M}}}{\mathrm{2}}+\mathrm{2}\boldsymbol{{m}}+\frac{{I}}{\mathrm{2}\boldsymbol{{R}}^{\mathrm{2}} }\right)} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\left(\mathrm{8}−\mathrm{2}\right)\left(\mathrm{10}\right)}{\left(\mathrm{4}+\mathrm{2}+\mathrm{2}\right)}\:{m}/{s}^{\mathrm{2}} \:=\frac{\mathrm{15}}{\mathrm{2}}\boldsymbol{{m}}/\boldsymbol{{s}}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\frac{\mathrm{30}}{{x}}\:=\:\frac{\mathrm{15}}{\mathrm{2}}\:\:{or}\:\:\:\boldsymbol{{x}}=\mathrm{4}\:. \\ $$$$ \\ $$
Commented by Physics lover last updated on 24/Oct/17
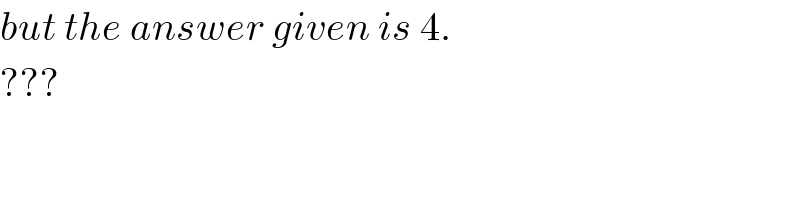
$${but}\:{the}\:{answer}\:{given}\:{is}\:\mathrm{4}. \\ $$$$??? \\ $$
Commented by Physics lover last updated on 24/Oct/17
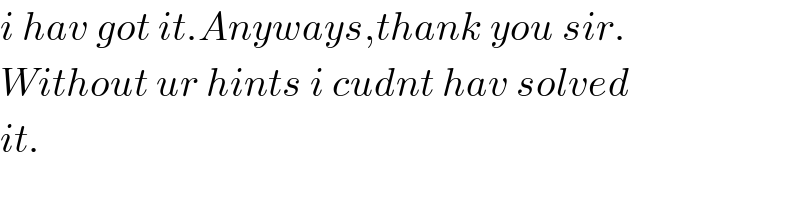
$${i}\:{hav}\:{got}\:{it}.{Anyways},{thank}\:{you}\:{sir}. \\ $$$${Without}\:{ur}\:{hints}\:{i}\:{cudnt}\:{hav}\:{solved} \\ $$$${it}. \\ $$
Answered by Physics lover last updated on 24/Oct/17
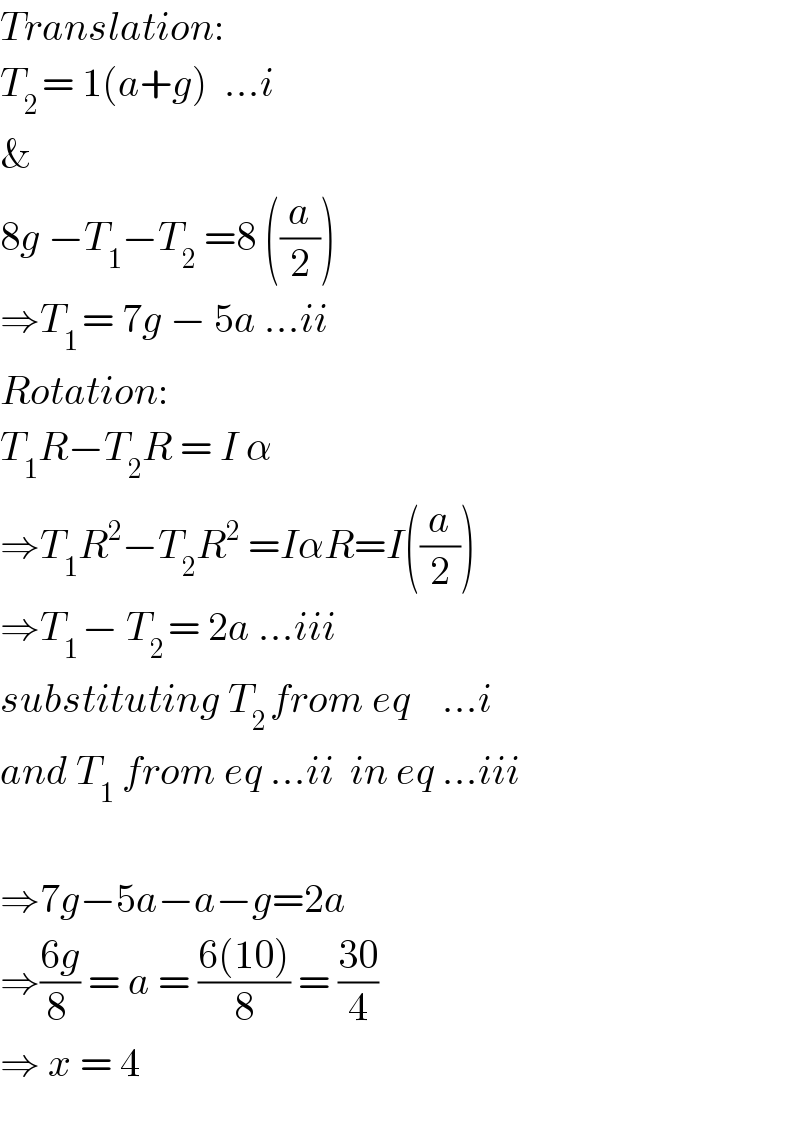
$${Translation}: \\ $$$${T}_{\mathrm{2}\:} =\:\mathrm{1}\left({a}+{g}\right)\:\:...{i} \\ $$$$\& \\ $$$$\mathrm{8}{g}\:−{T}_{\mathrm{1}} −{T}_{\mathrm{2}} \:=\mathrm{8}\:\left(\frac{{a}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{T}_{\mathrm{1}\:} =\:\mathrm{7}{g}\:−\:\mathrm{5}{a}\:...{ii} \\ $$$${Rotation}: \\ $$$${T}_{\mathrm{1}} {R}−{T}_{\mathrm{2}} {R}\:=\:{I}\:\alpha \\ $$$$\Rightarrow{T}_{\mathrm{1}} {R}^{\mathrm{2}} −{T}_{\mathrm{2}} {R}^{\mathrm{2}} \:={I}\alpha{R}={I}\left(\frac{{a}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{T}_{\mathrm{1}\:} −\:{T}_{\mathrm{2}\:} =\:\mathrm{2}{a}\:...{iii} \\ $$$${substituting}\:{T}_{\mathrm{2}\:} {from}\:{eq}\:\:\:\:...{i} \\ $$$${and}\:{T}_{\mathrm{1}} \:{from}\:{eq}\:...{ii}\:\:{in}\:{eq}\:...{iii} \\ $$$$ \\ $$$$\Rightarrow\mathrm{7}{g}−\mathrm{5}{a}−{a}−{g}=\mathrm{2}{a} \\ $$$$\Rightarrow\frac{\mathrm{6}{g}}{\mathrm{8}\:}\:=\:{a}\:=\:\frac{\mathrm{6}\left(\mathrm{10}\right)}{\mathrm{8}}\:=\:\frac{\mathrm{30}}{\mathrm{4}} \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{4} \\ $$$$ \\ $$
