
Question Number 22768 by math solver last updated on 22/Oct/17
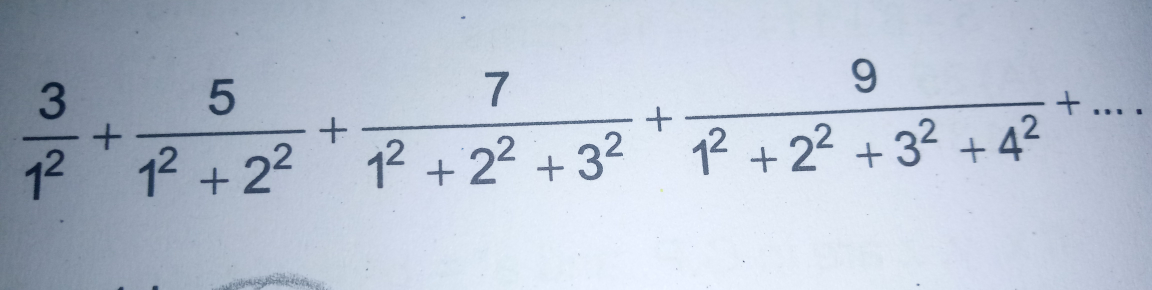
Commented by math solver last updated on 22/Oct/17
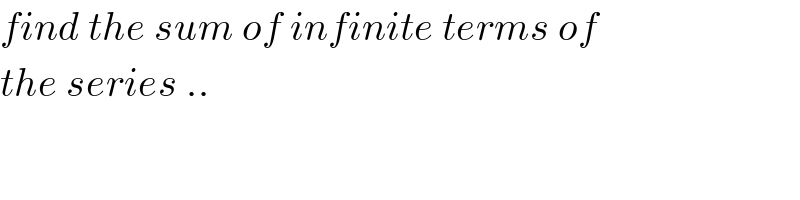
$${find}\:{the}\:{sum}\:{of}\:{infinite}\:{terms}\:{of}\: \\ $$$${the}\:{series}\:.. \\ $$
Commented by math solver last updated on 22/Oct/17
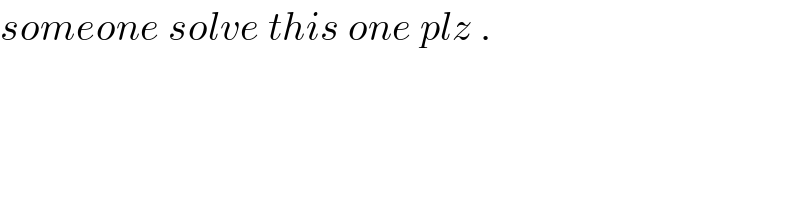
$${someone}\:{solve}\:{this}\:{one}\:{plz}\:. \\ $$
Answered by $@ty@m last updated on 22/Oct/17

$${N}^{{r}} {of}\:{t}_{{n}} =\mathrm{2}{n}+\mathrm{1} \\ $$$${D}^{{r}} {of}\:{t}_{{n}} =\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +...+{n}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\Sigma{n}^{\mathrm{2}} =\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}} \\ $$$$\left({you}\:{can}\:{find}\:{its}\:{proof}\:{in}\:{your}\:{textbook}\right) \\ $$$$ \\ $$$$\therefore\:{t}_{{n}} =\frac{\mathrm{6}\left(\mathrm{2}{n}+\mathrm{1}\right)}{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{6}}{{n}\left({n}+\mathrm{1}\right)} \\ $$$$=\mathrm{6}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$\therefore{S}_{{n}} =\mathrm{6}\left\{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\right)+.....+\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)\right\} \\ $$$$=\mathrm{6}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{6}{n}}{{n}+\mathrm{1}} \\ $$$${S}_{\infty} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\:\:\frac{\mathrm{6}{n}}{{n}+\mathrm{1}} \\ $$$${S}_{\infty} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\:\:\frac{\mathrm{6}}{\mathrm{1}+\frac{\mathrm{1}}{{n}}}=\mathrm{6}\:{Ans}. \\ $$
Commented by math solver last updated on 22/Oct/17
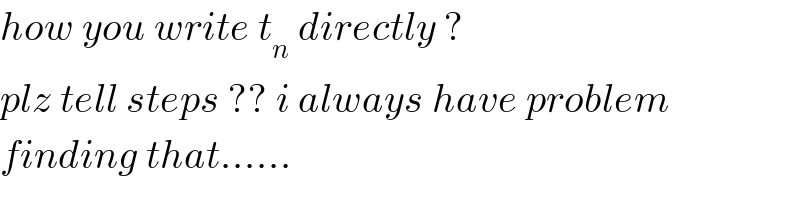
$${how}\:{you}\:{write}\:{t}_{{n}} \:{directly}\:? \\ $$$${plz}\:{tell}\:{steps}\:??\:{i}\:{always}\:{have}\:{problem} \\ $$$${finding}\:{that}...... \\ $$
Commented by $@ty@m last updated on 22/Oct/17

$${Is}\:{it}\:{clear}\:{now}? \\ $$
Commented by math solver last updated on 22/Oct/17

$${yes}\:\:,\:{thanks}\:{bro}! \\ $$
