
Question Number 21321 by Tinkutara last updated on 20/Sep/17
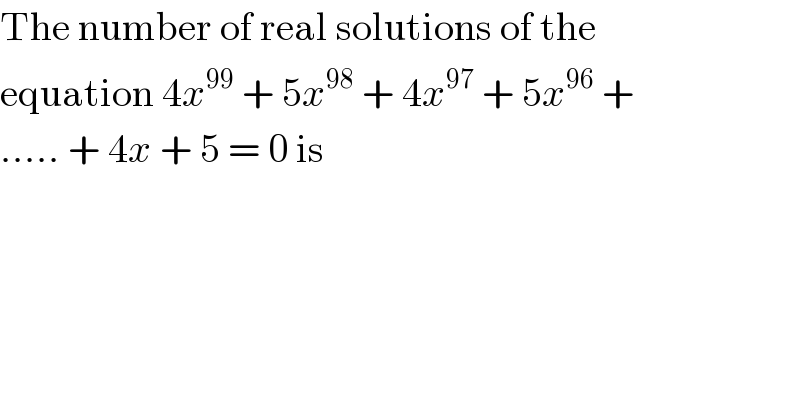
$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{real}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{equation}\:\mathrm{4}{x}^{\mathrm{99}} \:+\:\mathrm{5}{x}^{\mathrm{98}} \:+\:\mathrm{4}{x}^{\mathrm{97}} \:+\:\mathrm{5}{x}^{\mathrm{96}} \:+ \\ $$$$.....\:+\:\mathrm{4}{x}\:+\:\mathrm{5}\:=\:\mathrm{0}\:\mathrm{is} \\ $$
Answered by dioph last updated on 21/Sep/17
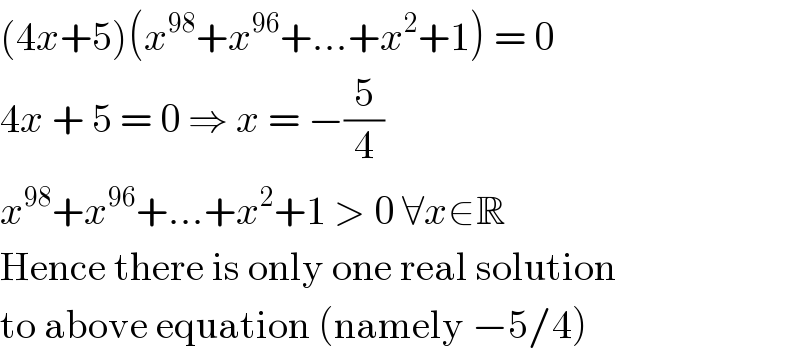
$$\left(\mathrm{4}{x}+\mathrm{5}\right)\left({x}^{\mathrm{98}} +{x}^{\mathrm{96}} +...+{x}^{\mathrm{2}} +\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{4}{x}\:+\:\mathrm{5}\:=\:\mathrm{0}\:\Rightarrow\:{x}\:=\:−\frac{\mathrm{5}}{\mathrm{4}} \\ $$$${x}^{\mathrm{98}} +{x}^{\mathrm{96}} +...+{x}^{\mathrm{2}} +\mathrm{1}\:>\:\mathrm{0}\:\forall{x}\in\mathbb{R} \\ $$$$\mathrm{Hence}\:\mathrm{there}\:\mathrm{is}\:\mathrm{only}\:\mathrm{one}\:\mathrm{real}\:\mathrm{solution} \\ $$$$\mathrm{to}\:\mathrm{above}\:\mathrm{equation}\:\left(\mathrm{namely}\:−\mathrm{5}/\mathrm{4}\right) \\ $$
Commented by Tinkutara last updated on 21/Sep/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
Commented by dioph last updated on 21/Sep/17

$$\mathrm{Degree}\:\mathrm{is}\:\mathrm{even}\:\left(\mathrm{98}\right),\:\mathrm{and}\:\mathrm{every}\:\mathrm{term} \\ $$$$\mathrm{is}\:\mathrm{positive}\:\left(+\mathrm{1}\right)\:\mathrm{so}\:\mathrm{the}\:\mathrm{functions} \\ $$$$\mathrm{graph}\:\mathrm{never}\:\mathrm{gets}\:\mathrm{to}\:\mathrm{cross}\:\mathrm{the}\:{x}\:\mathrm{axis} \\ $$
Commented by $@ty@m last updated on 21/Sep/17
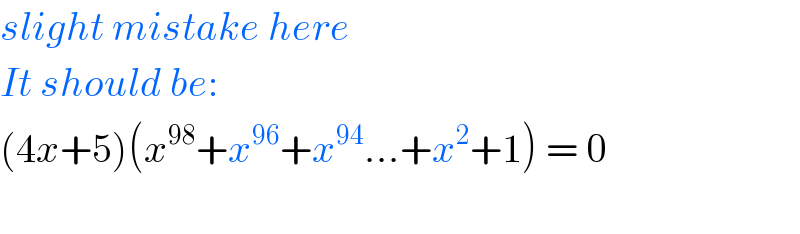
$${slight}\:{mistake}\:{here} \\ $$$${It}\:{should}\:{be}: \\ $$$$\left(\mathrm{4}{x}+\mathrm{5}\right)\left({x}^{\mathrm{98}} +{x}^{\mathrm{96}} +{x}^{\mathrm{94}} ...+{x}^{\mathrm{2}} +\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$ \\ $$
Commented by dioph last updated on 21/Sep/17

$$\mathrm{indeed},\:\mathrm{thanks}\:\mathrm{for}\:\mathrm{pointing}\:\mathrm{it}\:\mathrm{out}. \\ $$$$\mathrm{i}\:\mathrm{am}\:\mathrm{most}\:\mathrm{sorry}\:\mathrm{and}\:\mathrm{it}\:\mathrm{is}\:\mathrm{now}\:\mathrm{corrected} \\ $$
