
Question Number 21316 by Tinkutara last updated on 20/Sep/17
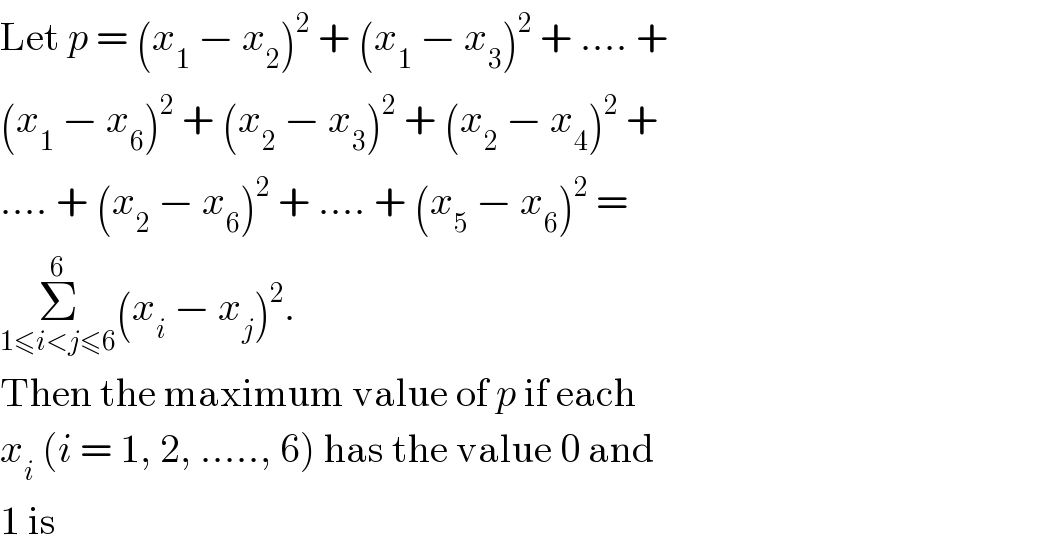
$$\mathrm{Let}\:{p}\:=\:\left({x}_{\mathrm{1}} \:−\:{x}_{\mathrm{2}} \right)^{\mathrm{2}} \:+\:\left({x}_{\mathrm{1}} \:−\:{x}_{\mathrm{3}} \right)^{\mathrm{2}} \:+\:....\:+ \\ $$ $$\left({x}_{\mathrm{1}} \:−\:{x}_{\mathrm{6}} \right)^{\mathrm{2}} \:+\:\left({x}_{\mathrm{2}} \:−\:{x}_{\mathrm{3}} \right)^{\mathrm{2}} \:+\:\left({x}_{\mathrm{2}} \:−\:{x}_{\mathrm{4}} \right)^{\mathrm{2}} \:+ \\ $$ $$....\:+\:\left({x}_{\mathrm{2}} \:−\:{x}_{\mathrm{6}} \right)^{\mathrm{2}} \:+\:....\:+\:\left({x}_{\mathrm{5}} \:−\:{x}_{\mathrm{6}} \right)^{\mathrm{2}} \:= \\ $$ $$\underset{\mathrm{1}\leqslant{i}<{j}\leqslant\mathrm{6}} {\overset{\mathrm{6}} {\sum}}\left({x}_{{i}} \:−\:{x}_{{j}} \right)^{\mathrm{2}} . \\ $$ $$\mathrm{Then}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{value}\:\mathrm{of}\:{p}\:\mathrm{if}\:\mathrm{each} \\ $$ $${x}_{{i}} \:\left({i}\:=\:\mathrm{1},\:\mathrm{2},\:.....,\:\mathrm{6}\right)\:\mathrm{has}\:\mathrm{the}\:\mathrm{value}\:\mathrm{0}\:\mathrm{and} \\ $$ $$\mathrm{1}\:\mathrm{is} \\ $$
