Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 211184 by nothing48 last updated on 30/Aug/24

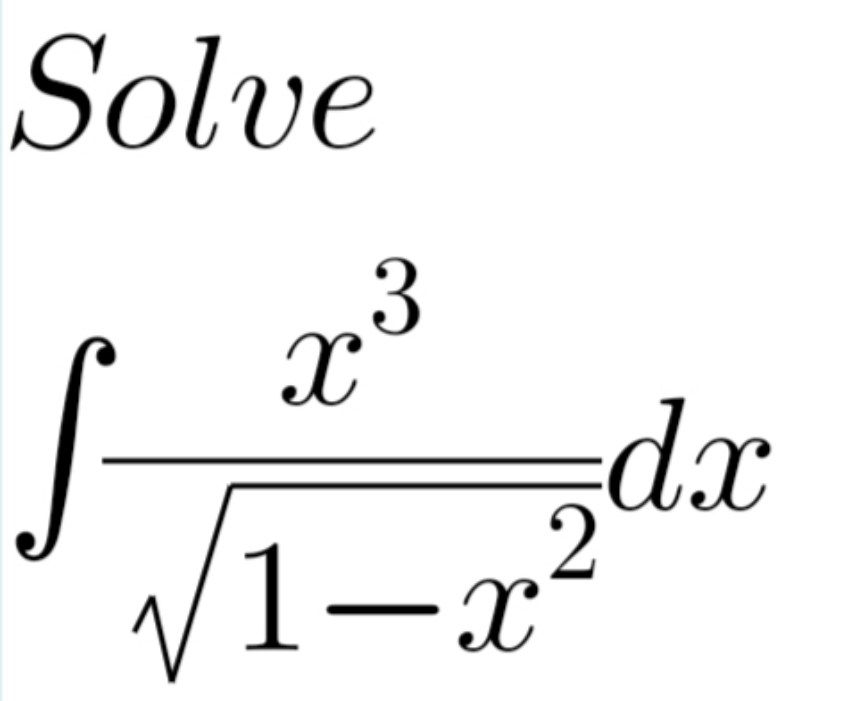
Answered by mm1342 last updated on 30/Aug/24

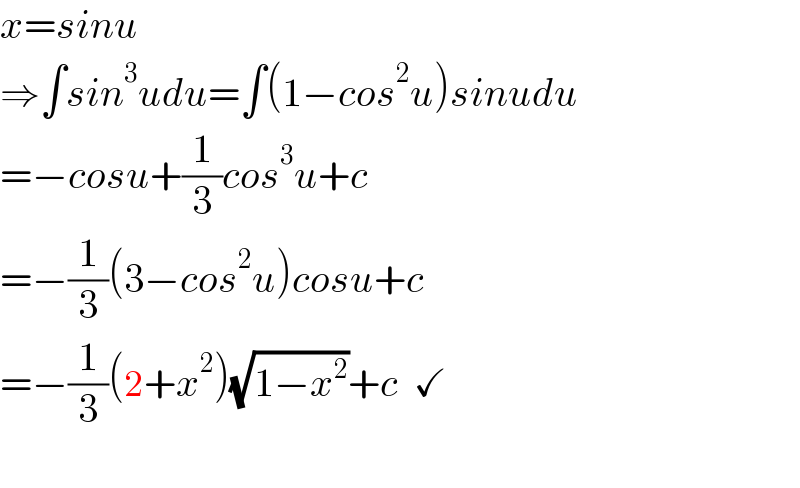
x=sinu ⇒∫sin^3 udu=∫(1−cos^2 u)sinudu =−cosu+(1/3)cos^3 u+c =−(1/3)(3−cos^2 u)cosu+c =−(1/3)(2+x^2 )(√(1−x^2 ))+c ✓

$${x}={sinu} \\ $$$$\Rightarrow\int{sin}^{\mathrm{3}} {udu}=\int\left(\mathrm{1}−{cos}^{\mathrm{2}} {u}\right){sinudu} \\ $$$$=−{cosu}+\frac{\mathrm{1}}{\mathrm{3}}{cos}^{\mathrm{3}} {u}+{c} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{3}−{cos}^{\mathrm{2}} {u}\right){cosu}+{c} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}+{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+{c}\:\:\checkmark \\ $$$$ \\ $$

Answered by Frix last updated on 30/Aug/24

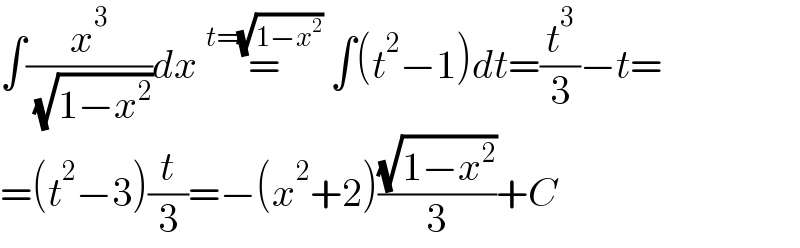
∫(x^3 /( (√(1−x^2 ))))dx =^(t=(√(1−x^2 ))) ∫(t^2 −1)dt=(t^3 /3)−t= =(t^2 −3)(t/3)=−(x^2 +2)((√(1−x^2 ))/3)+C

$$\int\frac{{x}^{\mathrm{3}} }{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}\:\overset{{t}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} {=}\:\int\left({t}^{\mathrm{2}} −\mathrm{1}\right){dt}=\frac{{t}^{\mathrm{3}} }{\mathrm{3}}−{t}= \\ $$$$=\left({t}^{\mathrm{2}} −\mathrm{3}\right)\frac{{t}}{\mathrm{3}}=−\left({x}^{\mathrm{2}} +\mathrm{2}\right)\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{3}}+{C} \\ $$

Commented by mm1342 last updated on 30/Aug/24

⌢

$$\:\underbrace{\frown} \\ $$

Commented by Frix last updated on 30/Aug/24

��

Answered by MathematicalUser2357 last updated on 27/Sep/24

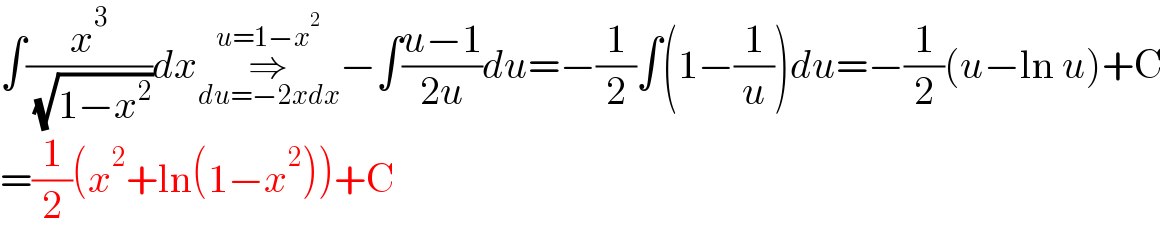
∫(x^3 /( (√(1−x^2 ))))dx⇒_(du=−2xdx) ^(u=1−x^2 ) −∫((u−1)/(2u))du=−(1/2)∫(1−(1/u))du=−(1/2)(u−ln u)+C =(1/2)(x^2 +ln(1−x^2 ))+C

$$\int\frac{{x}^{\mathrm{3}} }{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}\underset{{du}=−\mathrm{2}{xdx}} {\overset{{u}=\mathrm{1}−{x}^{\mathrm{2}} } {\Rightarrow}}−\int\frac{{u}−\mathrm{1}}{\mathrm{2}{u}}{du}=−\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{1}−\frac{\mathrm{1}}{{u}}\right){du}=−\frac{\mathrm{1}}{\mathrm{2}}\left({u}−\mathrm{ln}\:{u}\right)+\mathrm{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({x}^{\mathrm{2}} +\mathrm{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\right)+\mathrm{C} \\ $$

Commented by MathematicalUser2357 last updated on 27/Sep/24

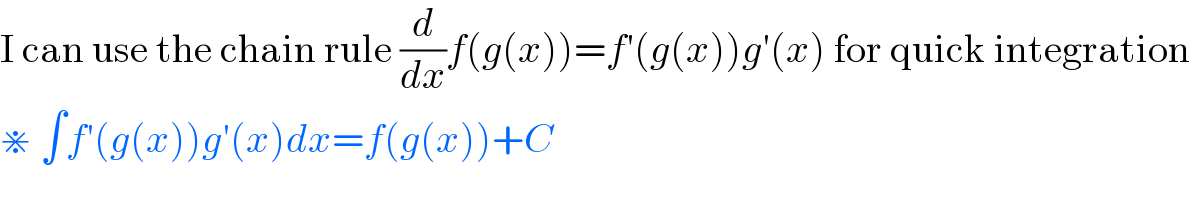
I can use the chain rule (d/dx)f(g(x))=f′(g(x))g′(x) for quick integration ⋇ ∫f′(g(x))g′(x)dx=f(g(x))+C

$$\mathrm{I}\:\mathrm{can}\:\mathrm{use}\:\mathrm{the}\:\mathrm{chain}\:\mathrm{rule}\:\frac{{d}}{{dx}}{f}\left({g}\left({x}\right)\right)={f}'\left({g}\left({x}\right)\right){g}'\left({x}\right)\:\mathrm{for}\:\mathrm{quick}\:\mathrm{integration} \\ $$$$\divideontimes\:\int{f}'\left({g}\left({x}\right)\right){g}'\left({x}\right){dx}={f}\left({g}\left({x}\right)\right)+{C} \\ $$

Commented by Frix last updated on 27/Sep/24

∫(x^3 /( (√(1−x^2 ))))dx =^([u=1−x^2 ]) (1/2)∫((u−1)/( (√u)))du= =(1/2)∫(u^(1/2) −u^(−(1/2)) )du=(u^(3/2) /3)−u^(1/2) =(((u−3)(√u))/3)= =−(((x^2 +2)(√(1−x^2 )))/3)+C

$$\int\frac{{x}^{\mathrm{3}} }{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}\:\overset{\left[{u}=\mathrm{1}−{x}^{\mathrm{2}} \right]} {=}\:\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{u}−\mathrm{1}}{\:\sqrt{{u}}}{du}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left({u}^{\frac{\mathrm{1}}{\mathrm{2}}} −{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \right){du}=\frac{{u}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}}−{u}^{\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\left({u}−\mathrm{3}\right)\sqrt{{u}}}{\mathrm{3}}= \\ $$$$=−\frac{\left({x}^{\mathrm{2}} +\mathrm{2}\right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{3}}+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com