Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 211157 by RojaTaniya last updated on 30/Aug/24

Commented by Rasheed.Sindhi last updated on 30/Aug/24

(x,y,z)=(1,0,0),(0,1,0),(0,0,1)

$$\left({x},{y},{z}\right)=\left(\mathrm{1},\mathrm{0},\mathrm{0}\right),\left(\mathrm{0},\mathrm{1},\mathrm{0}\right),\left(\mathrm{0},\mathrm{0},\mathrm{1}\right) \\ $$

Answered by Rasheed.Sindhi last updated on 30/Aug/24

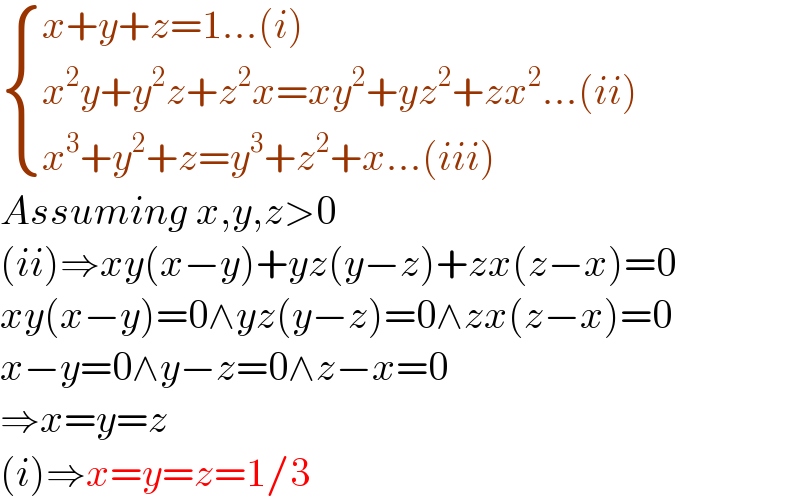
{ ((x+y+z=1...(i))),((x^2 y+y^2 z+z^2 x=xy^2 +yz^2 +zx^2 ...(ii))),((x^3 +y^2 +z=y^3 +z^2 +x...(iii))) :} Assuming x,y,z>0 (ii)⇒xy(x−y)+yz(y−z)+zx(z−x)=0 xy(x−y)=0∧yz(y−z)=0∧zx(z−x)=0 x−y=0∧y−z=0∧z−x=0 ⇒x=y=z (i)⇒x=y=z=1/3

$$\begin{cases}{{x}+{y}+{z}=\mathrm{1}...\left({i}\right)}\\{{x}^{\mathrm{2}} {y}+{y}^{\mathrm{2}} {z}+{z}^{\mathrm{2}} {x}={xy}^{\mathrm{2}} +{yz}^{\mathrm{2}} +{zx}^{\mathrm{2}} ...\left({ii}\right)}\\{{x}^{\mathrm{3}} +{y}^{\mathrm{2}} +{z}={y}^{\mathrm{3}} +{z}^{\mathrm{2}} +{x}...\left({iii}\right)}\end{cases} \\ $$$${Assuming}\:{x},{y},{z}>\mathrm{0} \\ $$$$\left({ii}\right)\Rightarrow{xy}\left({x}−{y}\right)+{yz}\left({y}−{z}\right)+{zx}\left({z}−{x}\right)=\mathrm{0} \\ $$$${xy}\left({x}−{y}\right)=\mathrm{0}\wedge{yz}\left({y}−{z}\right)=\mathrm{0}\wedge{zx}\left({z}−{x}\right)=\mathrm{0} \\ $$$${x}−{y}=\mathrm{0}\wedge{y}−{z}=\mathrm{0}\wedge{z}−{x}=\mathrm{0} \\ $$$$\Rightarrow{x}={y}={z} \\ $$$$\left({i}\right)\Rightarrow{x}={y}={z}=\mathrm{1}/\mathrm{3} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com