
Question Number 21077 by j.masanja06@gmail.com last updated on 11/Sep/17
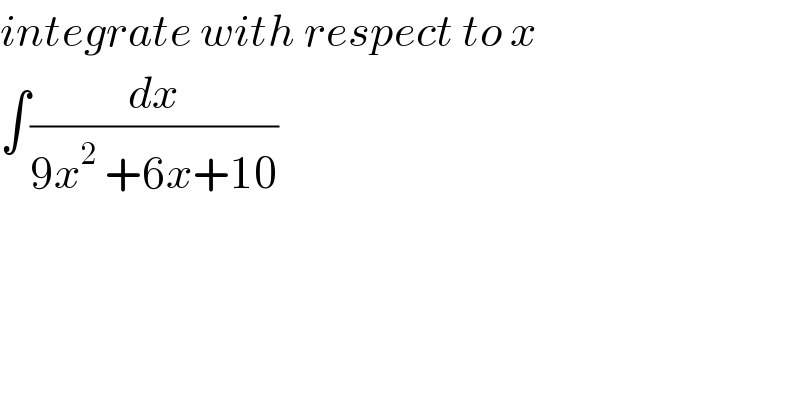
$${integrate}\:{with}\:{respect}\:{to}\:{x} \\ $$$$\int\frac{{dx}}{\mathrm{9}{x}^{\mathrm{2}} \:+\mathrm{6}{x}+\mathrm{10}} \\ $$
Answered by Joel577 last updated on 12/Sep/17
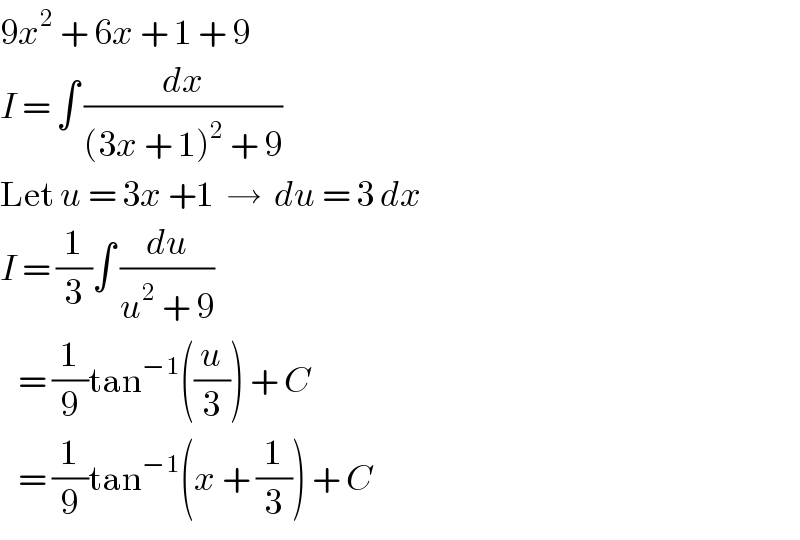
$$\mathrm{9}{x}^{\mathrm{2}} \:+\:\mathrm{6}{x}\:+\:\mathrm{1}\:+\:\mathrm{9} \\ $$$${I}\:=\:\int\:\frac{{dx}}{\left(\mathrm{3}{x}\:+\:\mathrm{1}\right)^{\mathrm{2}} \:+\:\mathrm{9}} \\ $$$$\mathrm{Let}\:{u}\:=\:\mathrm{3}{x}\:+\mathrm{1}\:\:\rightarrow\:\:{du}\:=\:\mathrm{3}\:{dx} \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{{du}}{{u}^{\mathrm{2}} \:+\:\mathrm{9}} \\ $$$$\:\:\:=\:\frac{\mathrm{1}}{\mathrm{9}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{u}}{\mathrm{3}}\right)\:+\:{C} \\ $$$$\:\:\:=\:\frac{\mathrm{1}}{\mathrm{9}}\mathrm{tan}^{−\mathrm{1}} \left({x}\:+\:\frac{\mathrm{1}}{\mathrm{3}}\right)\:+\:{C} \\ $$
