
Question Number 210524 by hardmath last updated on 11/Aug/24

Commented by hardmath last updated on 11/Aug/24

$$\boldsymbol{\mathrm{r}}\:=\:? \\ $$
Answered by mr W last updated on 12/Aug/24
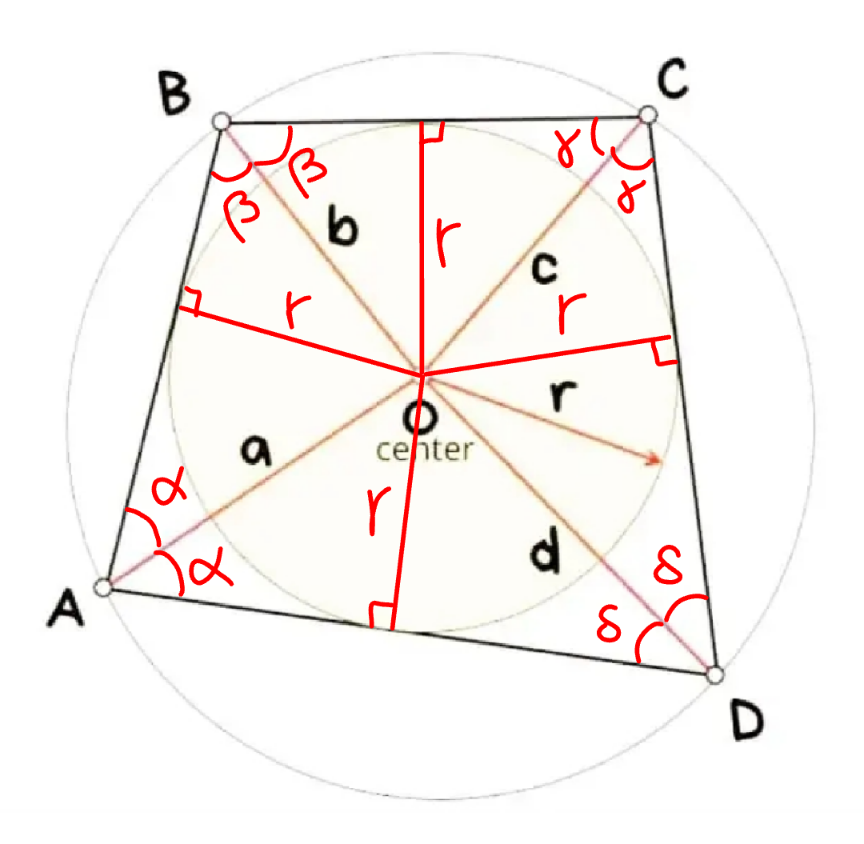
Commented by mr W last updated on 12/Aug/24
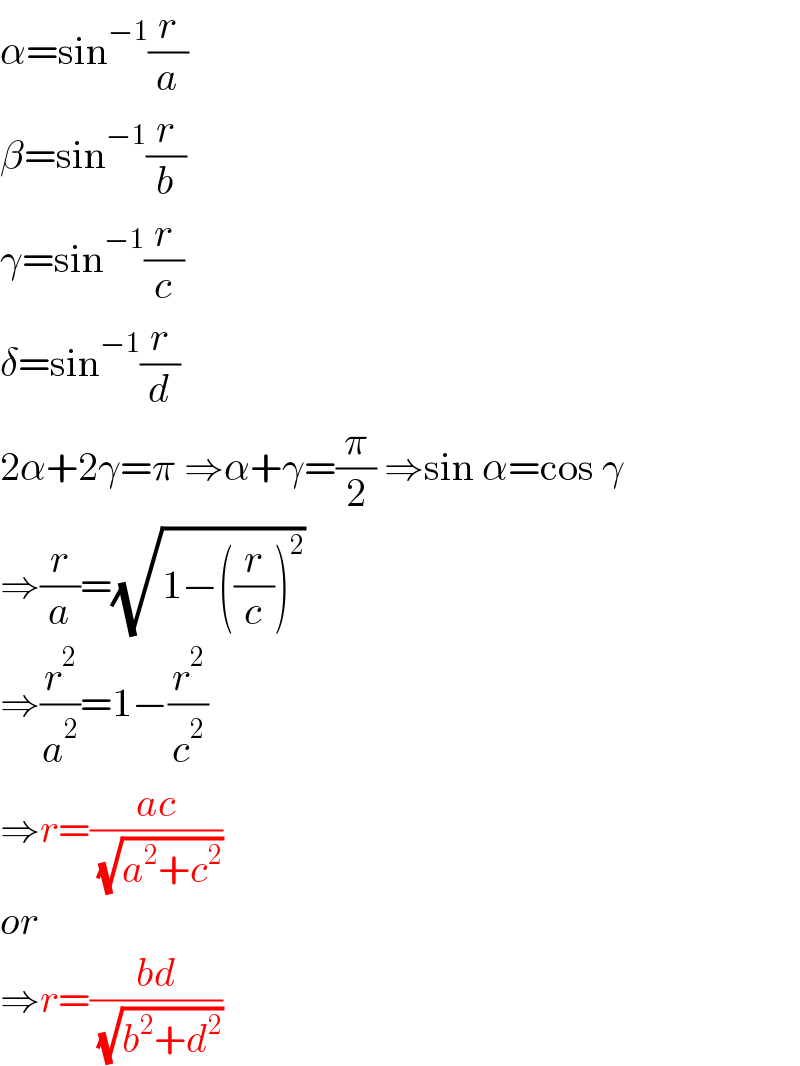
$$\alpha=\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{a}} \\ $$$$\beta=\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{b}} \\ $$$$\gamma=\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{c}} \\ $$$$\delta=\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{d}} \\ $$$$\mathrm{2}\alpha+\mathrm{2}\gamma=\pi\:\Rightarrow\alpha+\gamma=\frac{\pi}{\mathrm{2}}\:\Rightarrow\mathrm{sin}\:\alpha=\mathrm{cos}\:\gamma \\ $$$$\Rightarrow\frac{{r}}{{a}}=\sqrt{\mathrm{1}−\left(\frac{{r}}{{c}}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{r}^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{c}^{\mathrm{2}} } \\ $$$$\Rightarrow{r}=\frac{{ac}}{\:\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }} \\ $$$${or} \\ $$$$\Rightarrow{r}=\frac{{bd}}{\:\sqrt{{b}^{\mathrm{2}} +{d}^{\mathrm{2}} }} \\ $$
Commented by hardmath last updated on 12/Aug/24
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{cool} \\ $$
