Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 210355 by hardmath last updated on 08/Aug/24

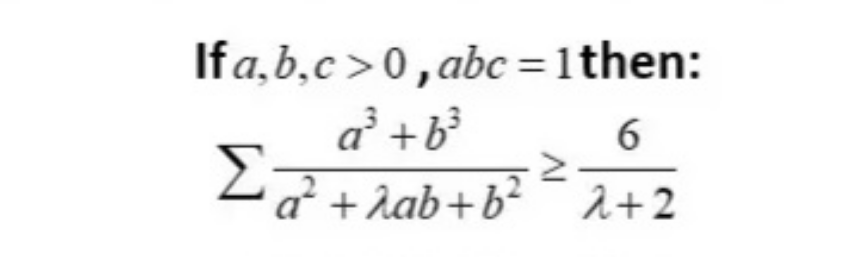
Answered by Berbere last updated on 08/Aug/24

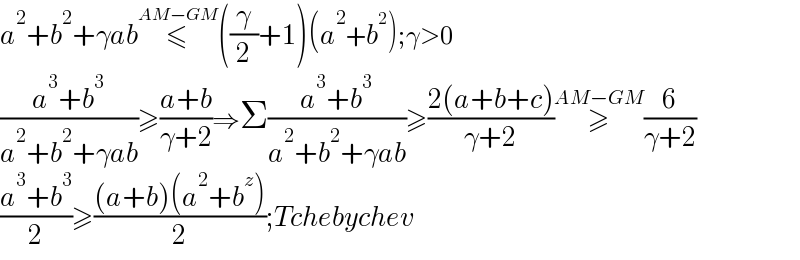
a^2 +b^2 +γab≤^(AM−GM) ((γ/2)+1)(a^2 +b^2 );γ>0 ((a^3 +b^3 )/(a^2 +b^2 +γab))≥((a+b)/(γ+2))⇒Σ((a^3 +b^3 )/(a^2 +b^2 +γab))≥((2(a+b+c))/(γ+2))≥^(AM−GM) (6/(γ+2)) ((a^3 +b^3 )/2)≥(((a+b)(a^2 +b^z ))/2);Tchebychev

$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\gamma{ab}\overset{{AM}−{GM}} {\leqslant}\left(\frac{\gamma}{\mathrm{2}}+\mathrm{1}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right);\gamma>\mathrm{0} \\ $$$$\frac{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\gamma{ab}}\geqslant\frac{{a}+{b}}{\gamma+\mathrm{2}}\Rightarrow\Sigma\frac{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\gamma{ab}}\geqslant\frac{\mathrm{2}\left({a}+{b}+{c}\right)}{\gamma+\mathrm{2}}\overset{{AM}−{GM}} {\geqslant}\frac{\mathrm{6}}{\gamma+\mathrm{2}} \\ $$$$\frac{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} }{\mathrm{2}}\geqslant\frac{\left({a}+{b}\right)\left({a}^{\mathrm{2}} +{b}^{{z}} \right)}{\mathrm{2}};{Tchebychev} \\ $$

Commented by hardmath last updated on 08/Aug/24

thank you dear professor cool

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{cool} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com