
Question Number 209880 by mnjuly1970 last updated on 24/Jul/24

Answered by mahdipoor last updated on 25/Jul/24
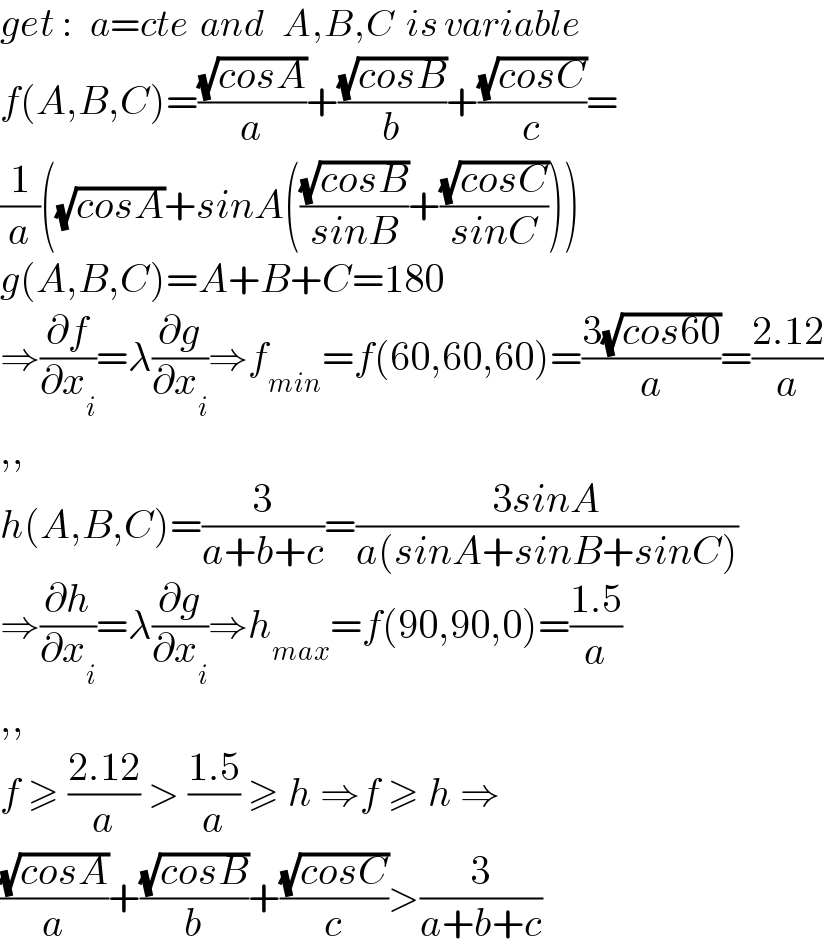
$${get}\::\:\:\:{a}={cte}\:\:{and}\:\:\:{A},{B},{C}\:\:{is}\:{variable} \\ $$$${f}\left({A},{B},{C}\right)=\frac{\sqrt{{cosA}}}{{a}}+\frac{\sqrt{{cosB}}}{{b}}+\frac{\sqrt{{cosC}}}{{c}}= \\ $$$$\frac{\mathrm{1}}{{a}}\left(\sqrt{{cosA}}+{sinA}\left(\frac{\sqrt{{cosB}}}{{sinB}}+\frac{\sqrt{{cosC}}}{{sinC}}\right)\right) \\ $$$${g}\left({A},{B},{C}\right)={A}+{B}+{C}=\mathrm{180} \\ $$$$\Rightarrow\frac{\partial{f}}{\partial{x}_{{i}} }=\lambda\frac{\partial{g}}{\partial{x}_{{i}} }\Rightarrow{f}_{{min}} ={f}\left(\mathrm{60},\mathrm{60},\mathrm{60}\right)=\frac{\mathrm{3}\sqrt{{cos}\mathrm{60}}}{{a}}=\frac{\mathrm{2}.\mathrm{12}}{{a}} \\ $$$$,, \\ $$$${h}\left({A},{B},{C}\right)=\frac{\mathrm{3}}{{a}+{b}+{c}}=\frac{\mathrm{3}{sinA}}{{a}\left({sinA}+{sinB}+{sinC}\right)} \\ $$$$\Rightarrow\frac{\partial{h}}{\partial{x}_{{i}} }=\lambda\frac{\partial{g}}{\partial{x}_{{i}} }\Rightarrow{h}_{{max}} ={f}\left(\mathrm{90},\mathrm{90},\mathrm{0}\right)=\frac{\mathrm{1}.\mathrm{5}}{{a}} \\ $$$$,, \\ $$$${f}\:\geqslant\:\frac{\mathrm{2}.\mathrm{12}}{{a}}\:>\:\frac{\mathrm{1}.\mathrm{5}}{{a}}\:\geqslant\:{h}\:\Rightarrow{f}\:\geqslant\:{h}\:\Rightarrow \\ $$$$\frac{\sqrt{{cosA}}}{{a}}+\frac{\sqrt{{cosB}}}{{b}}+\frac{\sqrt{{cosC}}}{{c}}>\frac{\mathrm{3}}{{a}+{b}+{c}} \\ $$
