
Question Number 209852 by hardmath last updated on 23/Jul/24
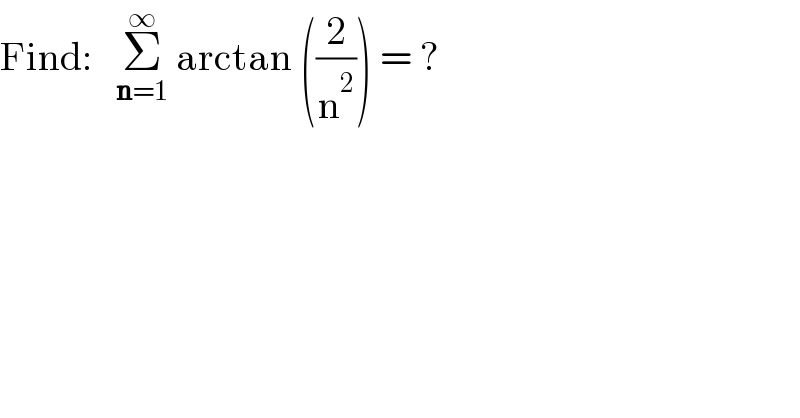
$$\mathrm{Find}:\:\:\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\mathrm{arctan}\:\left(\frac{\mathrm{2}}{\mathrm{n}^{\mathrm{2}} }\right)\:=\:? \\ $$
Answered by mr W last updated on 24/Jul/24
![(2/n^2 )=(((n+1)−(n−1))/(1+(n+1)(n−1))) say tan α=n+1, tan β=n−1, then (((n+1)−(n−1))/(1+(n+1)(n−1)))=((tan α−tan β)/(1+tan α tan β))=tan (α−β) i.e. tan (α−β)=(2/n^2 ), or tan^(−1) (2/n^2 )=α−β=tan^(−1) (n+1)−tan^(−1) (n−1) Σ_(n=1) ^∞ tan^(−1) (2/n^2 ) =lim_(n→∞) Σ_(k=1) ^n tan^(−1) (2/k^2 ) =lim_(n→∞) Σ_(k=1) ^n [tan^(−1) (k+1)−tan^(−1) (k−1)] =lim_(n→∞) {[tan^(−1) 2+tan^(−1) 3+...+tan^(−1) n+tan^(−1) (n+1)]−[tan^(−1) 0+tan^(−1) 1+tan^(−1) 2+...+tan^(−1) (n−1)]} =lim_(n→∞) {[tan^(−1) n+tan^(−1) (n+1)]−[tan^(−1) 0+tan^(−1) 1} =lim_(n→∞) {tan^(−1) n+tan^(−1) (n+1)−0−(π/4)} =(π/2)+(π/2)−0−(π/4) =((3π)/4) ✓](Q209869.png)
$$\frac{\mathrm{2}}{{n}^{\mathrm{2}} }=\frac{\left({n}+\mathrm{1}\right)−\left({n}−\mathrm{1}\right)}{\mathrm{1}+\left({n}+\mathrm{1}\right)\left({n}−\mathrm{1}\right)} \\ $$$${say}\:\mathrm{tan}\:\alpha={n}+\mathrm{1},\:\mathrm{tan}\:\beta={n}−\mathrm{1},\:{then} \\ $$$$\frac{\left({n}+\mathrm{1}\right)−\left({n}−\mathrm{1}\right)}{\mathrm{1}+\left({n}+\mathrm{1}\right)\left({n}−\mathrm{1}\right)}=\frac{\mathrm{tan}\:\alpha−\mathrm{tan}\:\beta}{\mathrm{1}+\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta}=\mathrm{tan}\:\left(\alpha−\beta\right) \\ $$$${i}.{e}.\:\mathrm{tan}\:\left(\alpha−\beta\right)=\frac{\mathrm{2}}{{n}^{\mathrm{2}} },\: \\ $$$${or}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}}{{n}^{\mathrm{2}} }=\alpha−\beta=\mathrm{tan}^{−\mathrm{1}} \left({n}+\mathrm{1}\right)−\mathrm{tan}^{−\mathrm{1}} \left({n}−\mathrm{1}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}}{{n}^{\mathrm{2}} } \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}}{{k}^{\mathrm{2}} } \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left[\mathrm{tan}^{−\mathrm{1}} \left({k}+\mathrm{1}\right)−\mathrm{tan}^{−\mathrm{1}} \left({k}−\mathrm{1}\right)\right] \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\left[\mathrm{tan}^{−\mathrm{1}} \mathrm{2}+\mathrm{tan}^{−\mathrm{1}} \mathrm{3}+...+\mathrm{tan}^{−\mathrm{1}} {n}+\mathrm{tan}^{−\mathrm{1}} \left({n}+\mathrm{1}\right)\right]−\left[\mathrm{tan}^{−\mathrm{1}} \mathrm{0}+\mathrm{tan}^{−\mathrm{1}} \mathrm{1}+\mathrm{tan}^{−\mathrm{1}} \mathrm{2}+...+\mathrm{tan}^{−\mathrm{1}} \left({n}−\mathrm{1}\right)\right]\right\} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\left[\mathrm{tan}^{−\mathrm{1}} {n}+\mathrm{tan}^{−\mathrm{1}} \left({n}+\mathrm{1}\right)\right]−\left[\mathrm{tan}^{−\mathrm{1}} \mathrm{0}+\mathrm{tan}^{−\mathrm{1}} \mathrm{1}\right\}\right. \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\mathrm{tan}^{−\mathrm{1}} {n}+\mathrm{tan}^{−\mathrm{1}} \left({n}+\mathrm{1}\right)−\mathrm{0}−\frac{\pi}{\mathrm{4}}\right\} \\ $$$$=\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}−\mathrm{0}−\frac{\pi}{\mathrm{4}} \\ $$$$=\frac{\mathrm{3}\pi}{\mathrm{4}}\:\checkmark \\ $$
Commented by hardmath last updated on 24/Jul/24
$$\mathrm{cool}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you} \\ $$
