Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 209234 by Tawa11 last updated on 04/Jul/24

Arrange in descending order: (√5) − (√2), (√7) − (√5) , (√(13)) − (√(11)) , (√(19)) − (√(17))

$$\mathrm{Arrange}\:\mathrm{in}\:\mathrm{descending}\:\mathrm{order}: \\ $$$$\:\:\:\:\sqrt{\mathrm{5}}\:\:−\:\:\sqrt{\mathrm{2}},\:\:\:\:\:\sqrt{\mathrm{7}}\:\:−\:\:\sqrt{\mathrm{5}}\:,\:\:\:\sqrt{\mathrm{13}}\:\:−\:\:\sqrt{\mathrm{11}}\:,\:\:\:\sqrt{\mathrm{19}}\:\:−\:\:\sqrt{\mathrm{17}} \\ $$

Answered by A5T last updated on 04/Jul/24

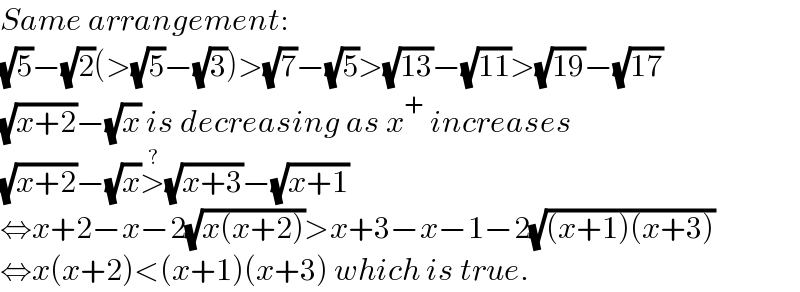
Same arrangement: (√5)−(√2)(>(√5)−(√3))>(√7)−(√5)>(√(13))−(√(11))>(√(19))−(√(17)) (√(x+2))−(√x) is decreasing as x^+ increases (√(x+2))−(√x)>^? (√(x+3))−(√(x+1)) ⇔x+2−x−2(√(x(x+2)))>x+3−x−1−2(√((x+1)(x+3))) ⇔x(x+2)<(x+1)(x+3) which is true.

$${Same}\:{arrangement}: \\ $$$$\sqrt{\mathrm{5}}−\sqrt{\mathrm{2}}\left(>\sqrt{\mathrm{5}}−\sqrt{\mathrm{3}}\right)>\sqrt{\mathrm{7}}−\sqrt{\mathrm{5}}>\sqrt{\mathrm{13}}−\sqrt{\mathrm{11}}>\sqrt{\mathrm{19}}−\sqrt{\mathrm{17}} \\ $$$$\sqrt{{x}+\mathrm{2}}−\sqrt{{x}}\:{is}\:{decreasing}\:{as}\:{x}^{+} \:{increases} \\ $$$$\sqrt{{x}+\mathrm{2}}−\sqrt{{x}}\overset{?} {>}\sqrt{{x}+\mathrm{3}}−\sqrt{{x}+\mathrm{1}} \\ $$$$\Leftrightarrow{x}+\mathrm{2}−{x}−\mathrm{2}\sqrt{{x}\left({x}+\mathrm{2}\right)}>{x}+\mathrm{3}−{x}−\mathrm{1}−\mathrm{2}\sqrt{\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right)} \\ $$$$\Leftrightarrow{x}\left({x}+\mathrm{2}\right)<\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right)\:{which}\:{is}\:{true}. \\ $$

Commented by Tawa11 last updated on 05/Jul/24

Thanks sir. I appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Answered by BaliramKumar last updated on 07/Jul/24

(√5)−(√2) = ((((√5)−(√2))((√5)+(√2)))/(((√5)+(√2)))) = (2/(((√5)+(√2)))) ...... (i) (√7)−(√5) = ((((√7)−(√5))((√7)+(√5)))/(((√7)+(√5)))) = (2/(((√7)+(√5)))) ......(ii) (√(13))−(√(11)) = ((((√(13))−(√(11)))((√(13))+(√(11))))/(((√(13))+(√(11))))) = (2/(((√(13))+(√(11))))) ...(iii) (√(19))−(√(17)) = ((((√(19))−(√(17)))((√(19))+(√(17))))/(((√(19))+(√(17))))) = (2/(((√(19))+(√(17))))) ....(iv) (i) > (ii) > (iii) > (iv)

$$\sqrt{\mathrm{5}}−\sqrt{\mathrm{2}}\:=\:\frac{\left(\sqrt{\mathrm{5}}−\sqrt{\mathrm{2}}\right)\left(\sqrt{\mathrm{5}}+\sqrt{\mathrm{2}}\right)}{\left(\sqrt{\mathrm{5}}+\sqrt{\mathrm{2}}\right)}\:\:=\:\frac{\mathrm{2}}{\left(\sqrt{\mathrm{5}}+\sqrt{\mathrm{2}}\right)}\:\:......\:\left(\mathrm{i}\right) \\ $$$$\sqrt{\mathrm{7}}−\sqrt{\mathrm{5}}\:=\:\frac{\left(\sqrt{\mathrm{7}}−\sqrt{\mathrm{5}}\right)\left(\sqrt{\mathrm{7}}+\sqrt{\mathrm{5}}\right)}{\left(\sqrt{\mathrm{7}}+\sqrt{\mathrm{5}}\right)}\:\:=\:\frac{\mathrm{2}}{\left(\sqrt{\mathrm{7}}+\sqrt{\mathrm{5}}\right)}\:\:......\left(\mathrm{ii}\right) \\ $$$$\sqrt{\mathrm{13}}−\sqrt{\mathrm{11}}\:=\:\frac{\left(\sqrt{\mathrm{13}}−\sqrt{\mathrm{11}}\right)\left(\sqrt{\mathrm{13}}+\sqrt{\mathrm{11}}\right)}{\left(\sqrt{\mathrm{13}}+\sqrt{\mathrm{11}}\right)}\:\:=\:\frac{\mathrm{2}}{\left(\sqrt{\mathrm{13}}+\sqrt{\mathrm{11}}\right)}\:...\left(\mathrm{iii}\right) \\ $$$$\sqrt{\mathrm{19}}−\sqrt{\mathrm{17}}\:=\:\frac{\left(\sqrt{\mathrm{19}}−\sqrt{\mathrm{17}}\right)\left(\sqrt{\mathrm{19}}+\sqrt{\mathrm{17}}\right)}{\left(\sqrt{\mathrm{19}}+\sqrt{\mathrm{17}}\right)}\:\:=\:\frac{\mathrm{2}}{\left(\sqrt{\mathrm{19}}+\sqrt{\mathrm{17}}\right)}\:....\left(\mathrm{iv}\right) \\ $$$$\left(\mathrm{i}\right)\:>\:\left(\mathrm{ii}\right)\:>\:\left(\mathrm{iii}\right)\:>\:\left(\mathrm{iv}\right) \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com