
Question Number 208842 by NasaSara last updated on 24/Jun/24
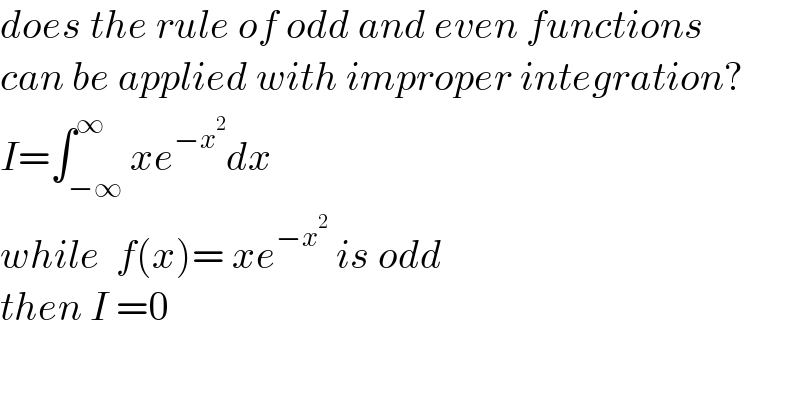
$${does}\:{the}\:{rule}\:{of}\:{odd}\:{and}\:{even}\:{functions}\: \\ $$$${can}\:{be}\:{applied}\:{with}\:{improper}\:{integration}? \\ $$$${I}=\int_{−\infty} ^{\infty} {xe}^{−{x}^{\mathrm{2}} } {dx}\: \\ $$$${while}\:\:{f}\left({x}\right)=\:{xe}^{−{x}^{\mathrm{2}} } \:{is}\:{odd} \\ $$$${then}\:{I}\:=\mathrm{0} \\ $$
Commented by Frix last updated on 24/Jun/24

$$\mathrm{Yes}. \\ $$
Answered by mathzup last updated on 24/Jun/24
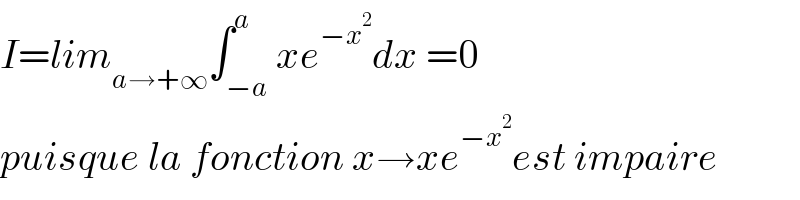
$${I}={lim}_{{a}\rightarrow+\infty} \int_{−{a}} ^{{a}} {xe}^{−{x}^{\mathrm{2}} } {dx}\:=\mathrm{0} \\ $$$${puisque}\:{la}\:{fonction}\:{x}\rightarrow{xe}^{−{x}^{\mathrm{2}} } {est}\:{impaire} \\ $$
