Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 208836 by Adeyemi889 last updated on 24/Jun/24

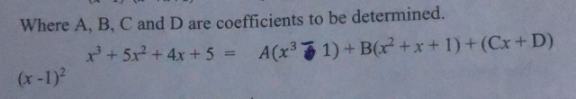
Answered by Rasheed.Sindhi last updated on 25/Jun/24

Ax^3 −A+Bx^2 +Bx+B+(Cx+D)(x^2 −2x+1) =Ax^3 −A+Bx^2 +Bx+B+Cx^3 +Dx^2 −2Cx^2 −2Dx+Cx+D =(A+C)x^3 +(B+D−2C)x^2 +(B−2D+C)x+(−A+B+D) =x^3 +5x^2 +4x+5 Comparing coefficients: A+C=1...i B+D−2C=5...ii B+C−2D=4...iii −A+B+D=5...iv iv ⇒B+D=A+5 ii ⇒ A+5−2C=5⇒A=2C i ⇒3C=1⇒C=1/3⇒A=2/3 iii ⇒B+C−2D=4 ⇒B+1/3−2D=4 ⇒B−2D=4−1/3=11/3 B+D=2/3+5=17/3 −3D=−6/3⇒D=2/3 B+D=17/3⇒B=17/3−2/3=5 ⇒B=5

$${Ax}^{\mathrm{3}} −{A}+{Bx}^{\mathrm{2}} +{Bx}+{B}+\left({Cx}+{D}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right) \\ $$$$={Ax}^{\mathrm{3}} −{A}+{Bx}^{\mathrm{2}} +{Bx}+{B}+{Cx}^{\mathrm{3}} +{Dx}^{\mathrm{2}} −\mathrm{2}{Cx}^{\mathrm{2}} −\mathrm{2}{Dx}+{Cx}+{D} \\ $$$$=\left({A}+{C}\right){x}^{\mathrm{3}} +\left({B}+{D}−\mathrm{2}{C}\right){x}^{\mathrm{2}} +\left({B}−\mathrm{2}{D}+{C}\right){x}+\left(−{A}+{B}+{D}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5} \\ $$$${Comparing}\:{coefficients}: \\ $$$${A}+{C}=\mathrm{1}...{i} \\ $$$${B}+{D}−\mathrm{2}{C}=\mathrm{5}...{ii} \\ $$$${B}+{C}−\mathrm{2}{D}=\mathrm{4}...{iii} \\ $$$$−{A}+{B}+{D}=\mathrm{5}...{iv} \\ $$$${iv}\:\Rightarrow{B}+{D}={A}+\mathrm{5} \\ $$$${ii}\:\Rightarrow\:{A}+\mathrm{5}−\mathrm{2}{C}=\mathrm{5}\Rightarrow{A}=\mathrm{2}{C} \\ $$$$\:{i}\:\Rightarrow\mathrm{3}{C}=\mathrm{1}\Rightarrow{C}=\mathrm{1}/\mathrm{3}\Rightarrow{A}=\mathrm{2}/\mathrm{3} \\ $$$${iii}\:\Rightarrow{B}+{C}−\mathrm{2}{D}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow{B}+\mathrm{1}/\mathrm{3}−\mathrm{2}{D}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow{B}−\mathrm{2}{D}=\mathrm{4}−\mathrm{1}/\mathrm{3}=\mathrm{11}/\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{B}+{D}=\mathrm{2}/\mathrm{3}+\mathrm{5}=\mathrm{17}/\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{3}{D}=−\mathrm{6}/\mathrm{3}\Rightarrow{D}=\mathrm{2}/\mathrm{3} \\ $$$${B}+{D}=\mathrm{17}/\mathrm{3}\Rightarrow{B}=\mathrm{17}/\mathrm{3}−\mathrm{2}/\mathrm{3}=\mathrm{5} \\ $$$$\Rightarrow{B}=\mathrm{5} \\ $$

Commented by Adeyemi889 last updated on 25/Jun/24

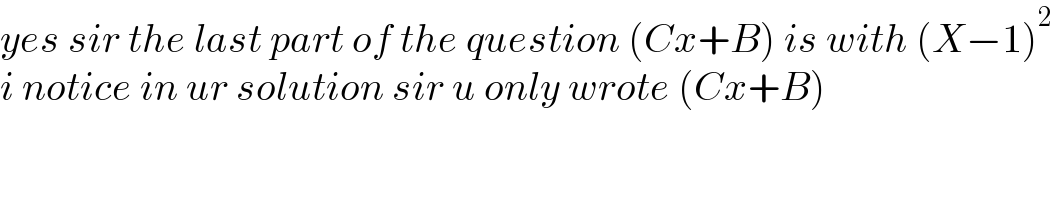
yes sir the last part of the question (Cx+B) is with (X−1)^2 i notice in ur solution sir u only wrote (Cx+B)

$${yes}\:{sir}\:{the}\:{last}\:{part}\:{of}\:{the}\:{question}\:\left({Cx}+{B}\right)\:{is}\:{with}\:\left({X}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$${i}\:{notice}\:{in}\:{ur}\:{solution}\:{sir}\:{u}\:{only}\:{wrote}\:\left({Cx}+{B}\right) \\ $$

Commented by Rasheed.Sindhi last updated on 25/Jun/24

Sorry sir, I didn′t notice (x−1)^2 which is on next line.I′ll go to correct it. Corrected

$${Sorry}\:{sir},\:{I}\:{didn}'{t}\:{notice}\:\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:{which} \\ $$$${is}\:{on}\:{next}\:{line}.{I}'{ll}\:{go}\:{to}\:{correct}\:{it}. \\ $$$${Corrected} \\ $$

Answered by Rasheed.Sindhi last updated on 25/Jun/24

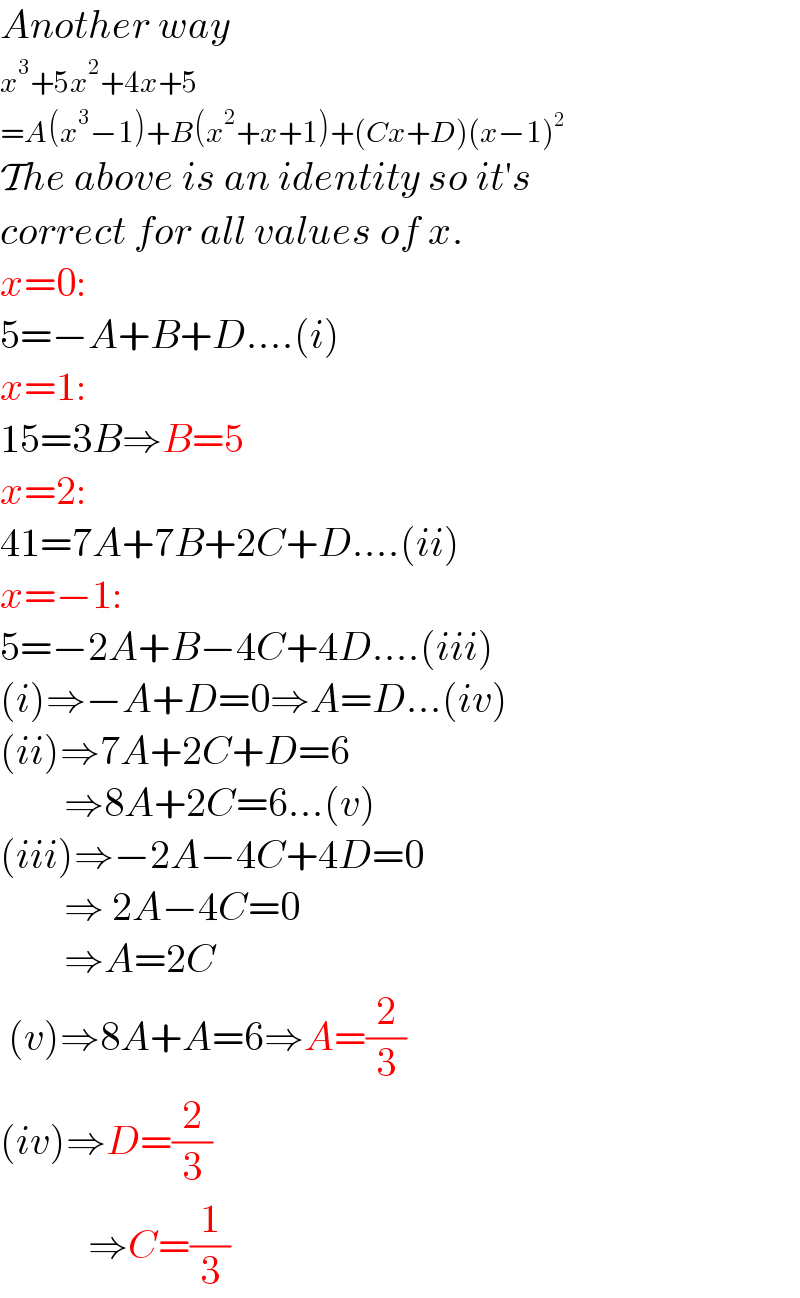
Another way x^3 +5x^2 +4x+5 =A(x^3 −1)+B(x^2 +x+1)+(Cx+D)(x−1)^2 The above is an identity so it′s correct for all values of x. x=0: 5=−A+B+D....(i) x=1: 15=3B⇒B=5 x=2: 41=7A+7B+2C+D....(ii) x=−1: 5=−2A+B−4C+4D....(iii) (i)⇒−A+D=0⇒A=D...(iv) (ii)⇒7A+2C+D=6 ⇒8A+2C=6...(v) (iii)⇒−2A−4C+4D=0 ⇒ 2A−4C=0 ⇒A=2C (v)⇒8A+A=6⇒A=(2/3) (iv)⇒D=(2/3) ⇒C=(1/3)

$${Another}\:{way} \\ $$$${x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5} \\ $$$$={A}\left({x}^{\mathrm{3}} −\mathrm{1}\right)+{B}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)+\left({Cx}+{D}\right)\left({x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathcal{T}{he}\:{above}\:{is}\:{an}\:{identity}\:{so}\:{it}'{s} \\ $$$${correct}\:{for}\:{all}\:{values}\:{of}\:{x}. \\ $$$${x}=\mathrm{0}: \\ $$$$\mathrm{5}=−{A}+{B}+{D}....\left({i}\right) \\ $$$${x}=\mathrm{1}: \\ $$$$\mathrm{15}=\mathrm{3}{B}\Rightarrow{B}=\mathrm{5} \\ $$$${x}=\mathrm{2}: \\ $$$$\mathrm{41}=\mathrm{7}{A}+\mathrm{7}{B}+\mathrm{2}{C}+{D}....\left({ii}\right) \\ $$$${x}=−\mathrm{1}: \\ $$$$\mathrm{5}=−\mathrm{2}{A}+{B}−\mathrm{4}{C}+\mathrm{4}{D}....\left({iii}\right) \\ $$$$\left({i}\right)\Rightarrow−{A}+{D}=\mathrm{0}\Rightarrow{A}={D}...\left({iv}\right) \\ $$$$\left({ii}\right)\Rightarrow\mathrm{7}{A}+\mathrm{2}{C}+{D}=\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow\mathrm{8}{A}+\mathrm{2}{C}=\mathrm{6}...\left({v}\right) \\ $$$$\left({iii}\right)\Rightarrow−\mathrm{2}{A}−\mathrm{4}{C}+\mathrm{4}{D}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow\:\mathrm{2}{A}−\mathrm{4}{C}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow{A}=\mathrm{2}{C} \\ $$$$\:\left({v}\right)\Rightarrow\mathrm{8}{A}+{A}=\mathrm{6}\Rightarrow{A}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\left({iv}\right)\Rightarrow{D}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{C}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$

Commented by Adeyemi889 last updated on 26/Jun/24

Thanks so much sir♥♥♥

$${Thanks}\:{so}\:{much}\:{sir}\heartsuit\heartsuit\heartsuit \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com