Question and Answers Forum

All Questions      Topic List

Operation Research Questions

Previous in All Question      Next in All Question      

Previous in Operation Research      Next in Operation Research      

Question Number 208608 by Tawa11 last updated on 18/Jun/24

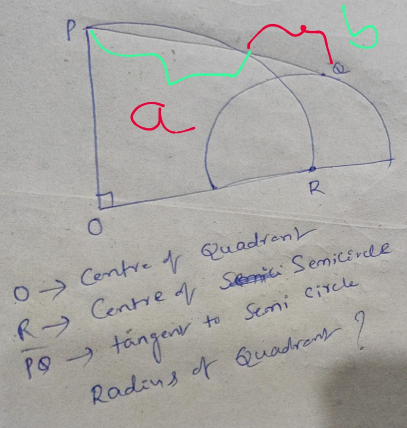
Answered by mr W last updated on 18/Jun/24

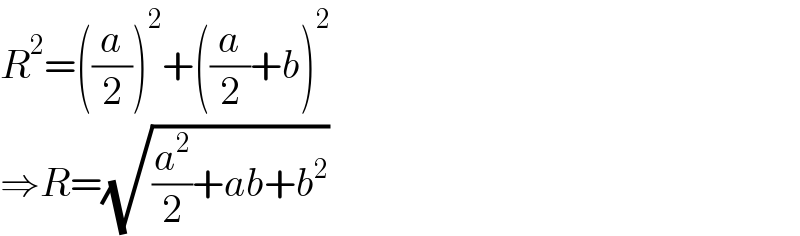
R^2 =((a/2))^2 +((a/2)+b)^2 ⇒R=(√((a^2 /2)+ab+b^2 ))

$${R}^{\mathrm{2}} =\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{a}}{\mathrm{2}}+{b}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{R}=\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+{ab}+{b}^{\mathrm{2}} } \\ $$

Commented by Tawa11 last updated on 18/Jun/24

Please sir, Show me the connection lines you used. Thanks sir

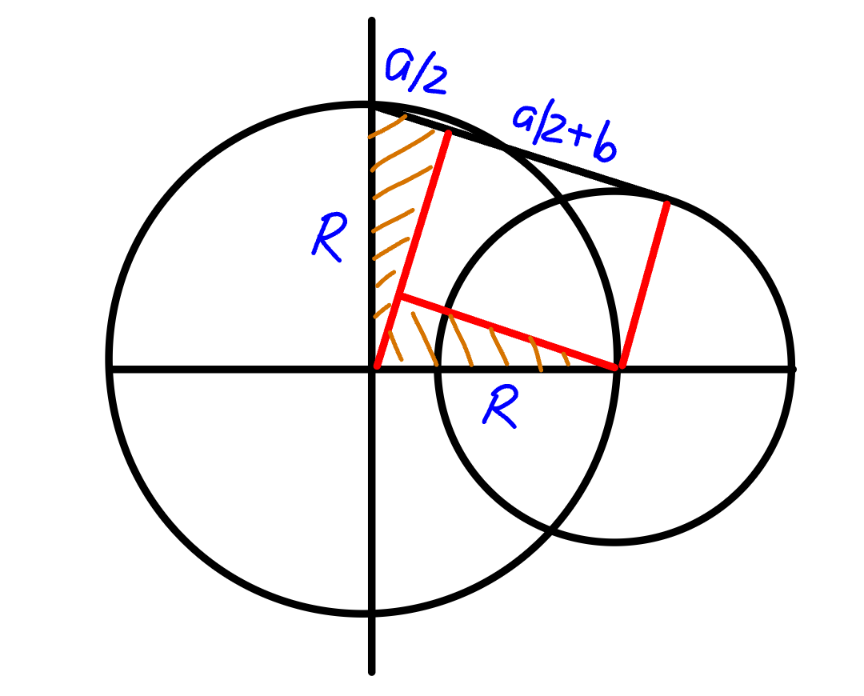
$$\mathrm{Please}\:\mathrm{sir}, \\ $$$$\mathrm{Show}\:\mathrm{me}\:\mathrm{the}\:\mathrm{connection}\:\mathrm{lines}\:\mathrm{you}\:\mathrm{used}. \\ $$$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Commented by mr W last updated on 18/Jun/24

Commented by Tawa11 last updated on 18/Jun/24

God bless you sir. I really appreciate

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate} \\ $$

Answered by efronzo1 last updated on 19/Jun/24

(√2) = (√((a+b)^2 +b^2 )) = (√((a^2 +2ab+2b^2 )/2))

$$\:\: \sqrt{\mathrm{2}}\:=\:\sqrt{\left({a}+{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\:\: =\:\sqrt{\frac{{a}^{\mathrm{2}} +\mathrm{2}{ab}+\mathrm{2}{b}^{\mathrm{2}} }{\mathrm{2}}}\: \\ $$

Commented by Tawa11 last updated on 19/Jun/24

Thanks sir

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com