Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 208594 by Jimenez000 last updated on 18/Jun/24

Find x+3^x <4

$${Find} \\ $$$${x}+\mathrm{3}^{{x}} <\mathrm{4} \\ $$

Answered by mr W last updated on 18/Jun/24

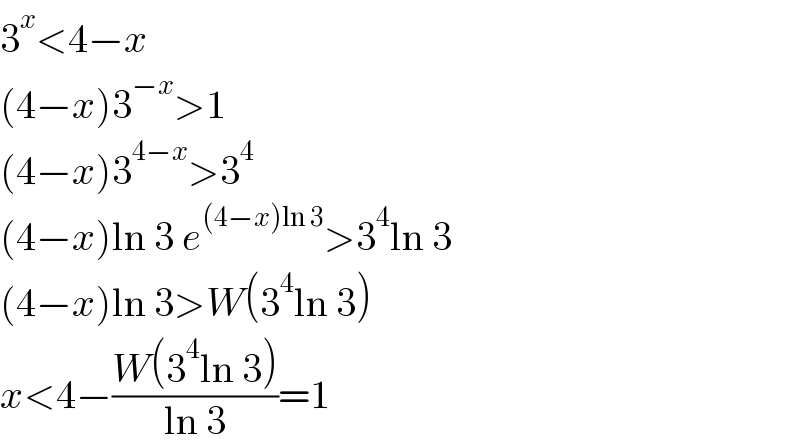
3^x <4−x (4−x)3^(−x) >1 (4−x)3^(4−x) >3^4 (4−x)ln 3 e^((4−x)ln 3) >3^4 ln 3 (4−x)ln 3>W(3^4 ln 3) x<4−((W(3^4 ln 3))/(ln 3))=1

$$\mathrm{3}^{{x}} <\mathrm{4}−{x} \\ $$$$\left(\mathrm{4}−{x}\right)\mathrm{3}^{−{x}} >\mathrm{1} \\ $$$$\left(\mathrm{4}−{x}\right)\mathrm{3}^{\mathrm{4}−{x}} >\mathrm{3}^{\mathrm{4}} \\ $$$$\left(\mathrm{4}−{x}\right)\mathrm{ln}\:\mathrm{3}\:{e}^{\left(\mathrm{4}−{x}\right)\mathrm{ln}\:\mathrm{3}} >\mathrm{3}^{\mathrm{4}} \mathrm{ln}\:\mathrm{3} \\ $$$$\left(\mathrm{4}−{x}\right)\mathrm{ln}\:\mathrm{3}>{W}\left(\mathrm{3}^{\mathrm{4}} \mathrm{ln}\:\mathrm{3}\right) \\ $$$${x}<\mathrm{4}−\frac{{W}\left(\mathrm{3}^{\mathrm{4}} \mathrm{ln}\:\mathrm{3}\right)}{\mathrm{ln}\:\mathrm{3}}=\mathrm{1} \\ $$

Commented by Jimenez000 last updated on 18/Jun/24

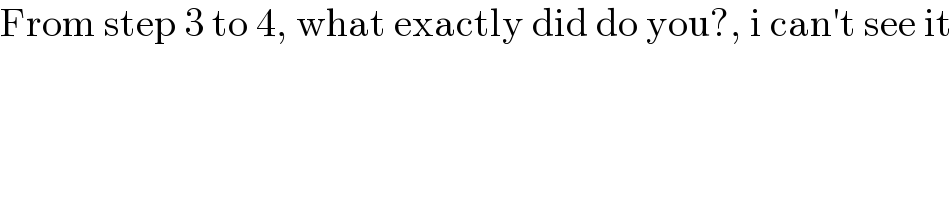
From step 3 to 4, what exactly did do you?, i can′t see it

$$\mathrm{From}\:\mathrm{step}\:\mathrm{3}\:\mathrm{to}\:\mathrm{4},\:\mathrm{what}\:\mathrm{exactly}\:\mathrm{did}\:\mathrm{do}\:\mathrm{you}?,\:\mathrm{i}\:\mathrm{can}'\mathrm{t}\:\mathrm{see}\:\mathrm{it} \\ $$

Commented by mr W last updated on 18/Jun/24

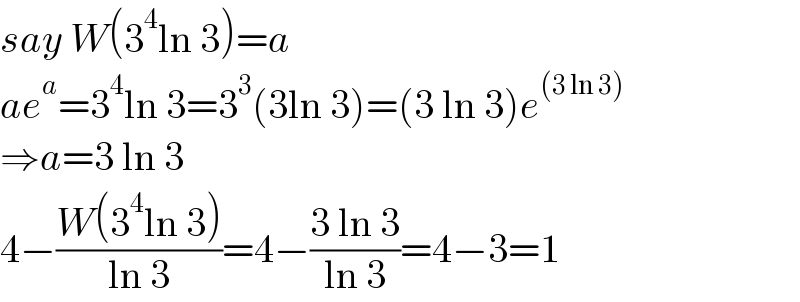
say W(3^4 ln 3)=a ae^a =3^4 ln 3=3^3 (3ln 3)=(3 ln 3)e^((3 ln 3)) ⇒a=3 ln 3 4−((W(3^4 ln 3))/(ln 3))=4−((3 ln 3)/(ln 3))=4−3=1

$${say}\:{W}\left(\mathrm{3}^{\mathrm{4}} \mathrm{ln}\:\mathrm{3}\right)={a} \\ $$$${ae}^{{a}} =\mathrm{3}^{\mathrm{4}} \mathrm{ln}\:\mathrm{3}=\mathrm{3}^{\mathrm{3}} \left(\mathrm{3ln}\:\mathrm{3}\right)=\left(\mathrm{3}\:\mathrm{ln}\:\mathrm{3}\right){e}^{\left(\mathrm{3}\:\mathrm{ln}\:\mathrm{3}\right)} \\ $$$$\Rightarrow{a}=\mathrm{3}\:\mathrm{ln}\:\mathrm{3} \\ $$$$\mathrm{4}−\frac{{W}\left(\mathrm{3}^{\mathrm{4}} \mathrm{ln}\:\mathrm{3}\right)}{\mathrm{ln}\:\mathrm{3}}=\mathrm{4}−\frac{\mathrm{3}\:\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{3}}=\mathrm{4}−\mathrm{3}=\mathrm{1} \\ $$

Commented by Jimenez000 last updated on 18/Jun/24

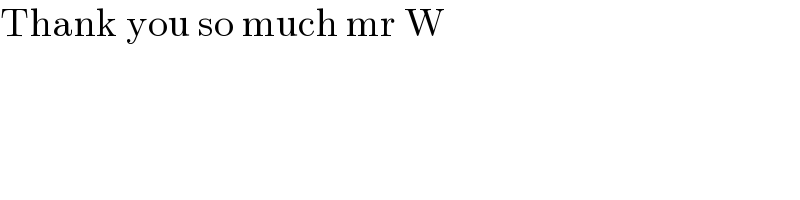
Thank you so much mr W

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{mr}\:\mathrm{W} \\ $$

Commented by Kademi last updated on 18/Jun/24

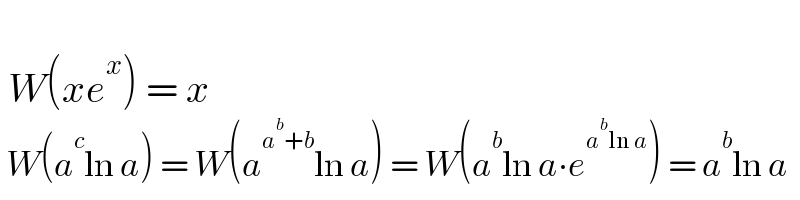
W(xe^x ) = x W(a^c ln a) = W(a^(a^b +b) ln a) = W(a^b ln a∙e^(a^b ln a) ) = a^b ln a

$$\: \\ $$$$\:{W}\left({xe}^{{x}} \right)\:=\:{x} \\ $$$$\:{W}\left({a}^{{c}} \mathrm{ln}\:{a}\right)\:=\:{W}\left({a}^{{a}^{{b}} +{b}} \mathrm{ln}\:{a}\right)\:=\:{W}\left({a}^{{b}} \mathrm{ln}\:{a}\centerdot{e}^{{a}^{{b}} \mathrm{ln}\:{a}} \right)\:=\:{a}^{{b}} \mathrm{ln}\:{a} \\ $$

Answered by Jimenez000 last updated on 18/Jun/24

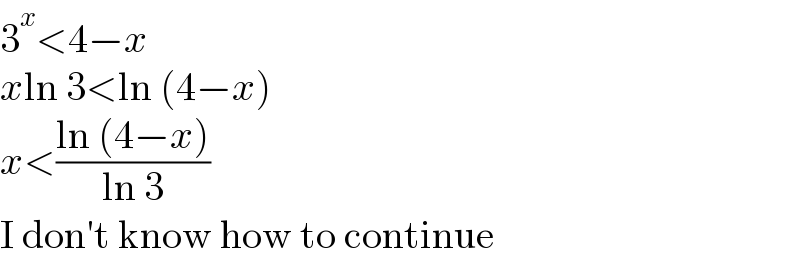
3^x <4−x xln 3<ln (4−x) x<((ln (4−x))/(ln 3)) I don′t know how to continue

$$\mathrm{3}^{{x}} <\mathrm{4}−{x} \\ $$$${x}\mathrm{ln}\:\mathrm{3}<\mathrm{ln}\:\left(\mathrm{4}−{x}\right) \\ $$$${x}<\frac{\mathrm{ln}\:\left(\mathrm{4}−{x}\right)}{\mathrm{ln}\:\mathrm{3}} \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{how}\:\mathrm{to}\:\mathrm{continue} \\ $$

Commented by Kademi last updated on 18/Jun/24

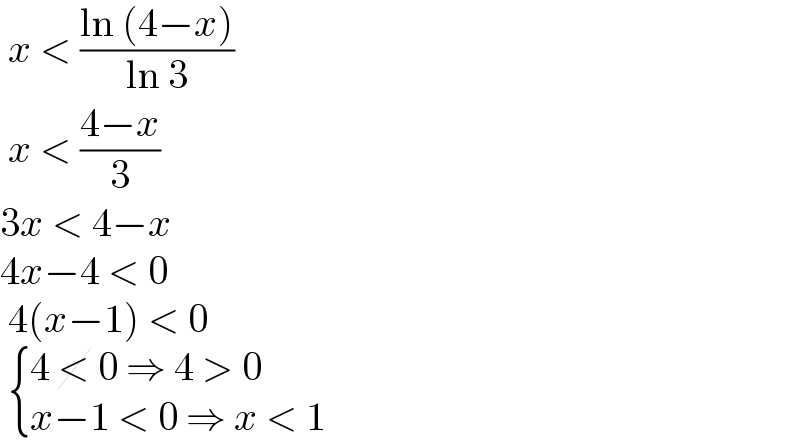
x < ((ln (4−x))/(ln 3)) x < ((4−x)/3) 3x < 4−x 4x−4 < 0 4(x−1) < 0 { ((4 < 0 ⇒ 4 > 0)),((x−1 < 0 ⇒ x < 1)) :}

$$\:{x}\:<\:\frac{\mathrm{ln}\:\left(\mathrm{4}−{x}\right)}{\mathrm{ln}\:\mathrm{3}} \\ $$$$\:{x}\:<\:\frac{\mathrm{4}−{x}}{\mathrm{3}} \\ $$$$\mathrm{3}{x}\:<\:\mathrm{4}−{x} \\ $$$$\mathrm{4}{x}−\mathrm{4}\:<\:\mathrm{0} \\ $$$$\:\mathrm{4}\left({x}−\mathrm{1}\right)\:<\:\mathrm{0} \\ $$$$\:\begin{cases}{\mathrm{4}\:\cancel{<}\:\mathrm{0}\:\Rightarrow\:\mathrm{4}\:>\:\mathrm{0}}\\{{x}−\mathrm{1}\:<\:\mathrm{0}\:\Rightarrow\:{x}\:<\:\mathrm{1}}\end{cases} \\ $$

Answered by mr W last updated on 18/Jun/24

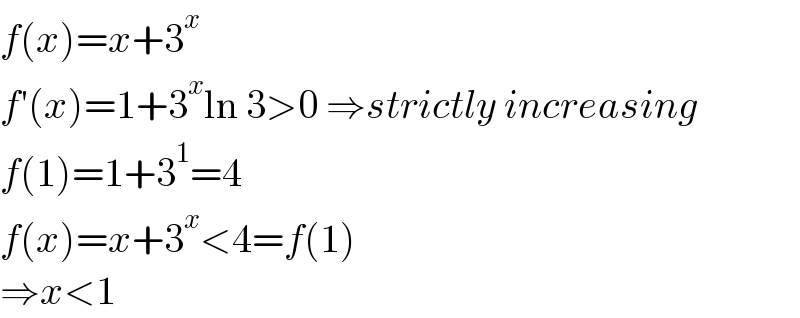
f(x)=x+3^x f′(x)=1+3^x ln 3>0 ⇒strictly increasing f(1)=1+3^1 =4 f(x)=x+3^x <4=f(1) ⇒x<1

$${f}\left({x}\right)={x}+\mathrm{3}^{{x}} \\ $$$${f}'\left({x}\right)=\mathrm{1}+\mathrm{3}^{{x}} \mathrm{ln}\:\mathrm{3}>\mathrm{0}\:\Rightarrow{strictly}\:{increasing} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1}+\mathrm{3}^{\mathrm{1}} =\mathrm{4} \\ $$$${f}\left({x}\right)={x}+\mathrm{3}^{{x}} <\mathrm{4}={f}\left(\mathrm{1}\right) \\ $$$$\Rightarrow{x}<\mathrm{1} \\ $$

Answered by Kademi last updated on 18/Jun/24

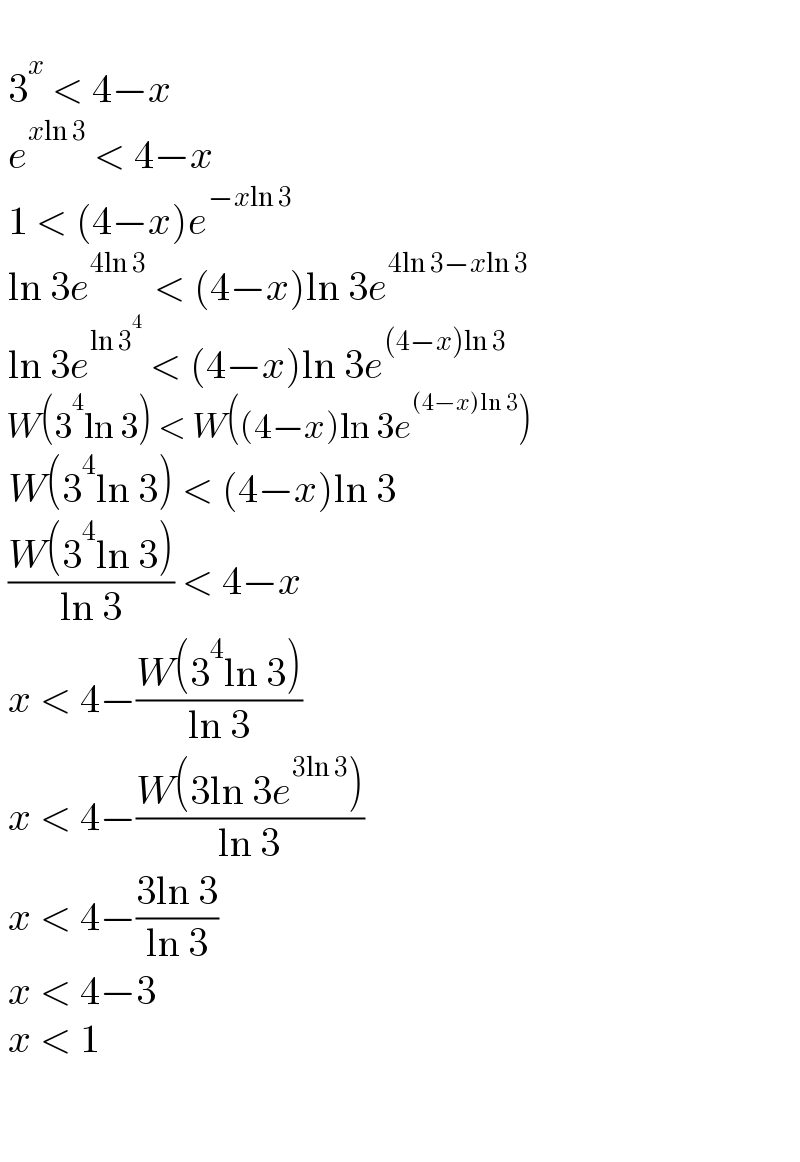
3^x < 4−x e^(xln 3) < 4−x 1 < (4−x)e^(−xln 3) ln 3e^(4ln 3) < (4−x)ln 3e^(4ln 3−xln 3) ln 3e^(ln 3^4 ) < (4−x)ln 3e^((4−x)ln 3) W(3^4 ln 3) < W((4−x)ln 3e^((4−x)ln 3) ) W(3^4 ln 3) < (4−x)ln 3 ((W(3^4 ln 3))/(ln 3)) < 4−x x < 4−((W(3^4 ln 3))/(ln 3)) x < 4−((W(3ln 3e^(3ln 3) ))/(ln 3)) x < 4−((3ln 3)/(ln 3)) x < 4−3 x < 1

$$\: \\ $$$$\:\mathrm{3}^{{x}} \:<\:\mathrm{4}−{x} \\ $$$$\:{e}^{{x}\mathrm{ln}\:\mathrm{3}} \:<\:\mathrm{4}−{x} \\ $$$$\:\mathrm{1}\:<\:\left(\mathrm{4}−{x}\right){e}^{−{x}\mathrm{ln}\:\mathrm{3}} \\ $$$$\:\mathrm{ln}\:\mathrm{3}{e}^{\mathrm{4ln}\:\mathrm{3}} \:<\:\left(\mathrm{4}−{x}\right)\mathrm{ln}\:\mathrm{3}{e}^{\mathrm{4ln}\:\mathrm{3}−{x}\mathrm{ln}\:\mathrm{3}} \\ $$$$\:\mathrm{ln}\:\mathrm{3}{e}^{\mathrm{ln}\:\mathrm{3}^{\mathrm{4}} } \:<\:\left(\mathrm{4}−{x}\right)\mathrm{ln}\:\mathrm{3}{e}^{\left(\mathrm{4}−{x}\right)\mathrm{ln}\:\mathrm{3}} \\ $$$$\:{W}\left(\mathrm{3}^{\mathrm{4}} \mathrm{ln}\:\mathrm{3}\right)\:<\:{W}\left(\left(\mathrm{4}−{x}\right)\mathrm{ln}\:\mathrm{3}{e}^{\left(\mathrm{4}−{x}\right)\mathrm{ln}\:\mathrm{3}} \right) \\ $$$$\:{W}\left(\mathrm{3}^{\mathrm{4}} \mathrm{ln}\:\mathrm{3}\right)\:<\:\left(\mathrm{4}−{x}\right)\mathrm{ln}\:\mathrm{3} \\ $$$$\:\frac{{W}\left(\mathrm{3}^{\mathrm{4}} \mathrm{ln}\:\mathrm{3}\right)}{\mathrm{ln}\:\mathrm{3}}\:<\:\mathrm{4}−{x} \\ $$$$\:{x}\:<\:\mathrm{4}−\frac{{W}\left(\mathrm{3}^{\mathrm{4}} \mathrm{ln}\:\mathrm{3}\right)}{\mathrm{ln}\:\mathrm{3}} \\ $$$$\:{x}\:<\:\mathrm{4}−\frac{{W}\left(\mathrm{3ln}\:\mathrm{3}{e}^{\mathrm{3ln}\:\mathrm{3}} \right)}{\mathrm{ln}\:\mathrm{3}} \\ $$$$\:{x}\:<\:\mathrm{4}−\frac{\mathrm{3ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{3}} \\ $$$$\:{x}\:<\:\mathrm{4}−\mathrm{3} \\ $$$$\:{x}\:<\:\mathrm{1} \\ $$$$\: \\ $$$$ \\ $$

Commented by Jimenez000 last updated on 18/Jun/24

Thank you Kademi

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Kademi} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com