
Previous in Relation and Functions Next in Relation and Functions
Question Number 208431 by alcohol last updated on 15/Jun/24
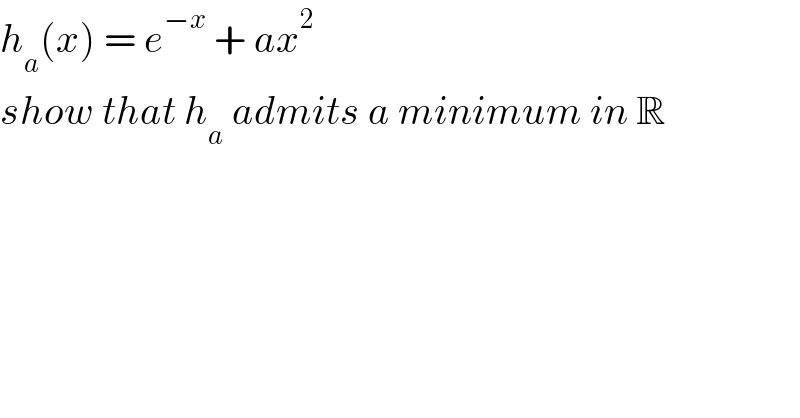
$${h}_{{a}} \left({x}\right)\:=\:{e}^{−{x}} \:+\:{ax}^{\mathrm{2}} \\ $$$${show}\:{that}\:{h}_{{a}} \:{admits}\:{a}\:{minimum}\:{in}\:\mathbb{R} \\ $$
Answered by mathzup last updated on 15/Jun/24
![cas 1 a>0 lim_(x→−∞) h(x)=+∞ lim_(x→+∞) h(x)=+∞ h^′ (x)=2ax−e^(−x) lim_(x→−∞) h^′ (x)=−∞ lim_(x→+∞) h^′ (x)=+∞ h^((2)) (x)=2a+e^(−x) >0 ⇒h^′ est strictement croissante x −∞ 0 α +∞ h^′ (x) −∞ → −1 → 0 +∞ ⇒∃ α / h^′ (α)=0 x −∞ α +∞ h^′ − 0 + h decr h(α) croi donc h possede un minimun qui est h(α)=e^(−α) +aα^2 h(0)=−1 and h(1)=e^(−1) +a>0 ⇒ α ∈]0,1[ rest a etudier les cas a<0 et a=0](Q208433.png)
$${cas}\:\mathrm{1}\:\:\:\:\:\:{a}>\mathrm{0} \\ $$$${lim}_{{x}\rightarrow−\infty} {h}\left({x}\right)=+\infty \\ $$$${lim}_{{x}\rightarrow+\infty} {h}\left({x}\right)=+\infty \\ $$$${h}^{'} \left({x}\right)=\mathrm{2}{ax}−{e}^{−{x}} \\ $$$${lim}_{{x}\rightarrow−\infty} \:\:{h}^{'} \left({x}\right)=−\infty \\ $$$${lim}_{{x}\rightarrow+\infty} \:\:{h}^{'} \left({x}\right)=+\infty \\ $$$${h}^{\left(\mathrm{2}\right)} \left({x}\right)=\mathrm{2}{a}+{e}^{−{x}} >\mathrm{0}\:\Rightarrow{h}^{'} \:{est}\:{strictement}\:{croissante} \\ $$$${x}\:\:\:\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\alpha\:\:\:\:\:\:\:+\infty \\ $$$${h}^{'} \left({x}\right)\:\:\:\:−\infty\:\rightarrow\:\:\:\:\:−\mathrm{1}\:\:\rightarrow\:\:\:\mathrm{0} \\ $$$$\:\:\:+\infty \\ $$$$\Rightarrow\exists\:\:\alpha\:\:\:\:/\:\:{h}^{'} \left(\alpha\right)=\mathrm{0} \\ $$$${x}\:\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\alpha\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$${h}^{'} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:+ \\ $$$${h}\:\:\:\:\:\:\:\:\:\:\:{decr}\:\:\:\:\:\:\:\:\:\:\:\:\:{h}\left(\alpha\right)\:\:\:\:\:{croi} \\ $$$${donc}\:{h}\:{possede}\:{un}\:{minimun}\:{qui}\:{est} \\ $$$${h}\left(\alpha\right)={e}^{−\alpha} \:+{a}\alpha^{\mathrm{2}} \\ $$$${h}\left(\mathrm{0}\right)=−\mathrm{1}\:{and}\:{h}\left(\mathrm{1}\right)={e}^{−\mathrm{1}} +{a}>\mathrm{0}\:\Rightarrow \\ $$$$\left.\alpha\:\in\right]\mathrm{0},\mathrm{1}\left[\right. \\ $$$${rest}\:{a}\:{etudier}\:{les}\:{cas}\:\:\:{a}<\mathrm{0}\:{et}\:{a}=\mathrm{0} \\ $$
Answered by Frix last updated on 16/Jun/24
![It′s not true for −(e/2)≤a≤0 a<−(e/2) ⇒ 1 local min plus 1 local max a=−(e/2) ⇒ 1 saddle point [ _(horizontal tangent)^(=1 point with a) ] −(e/2)<a≤0 ⇒ no min/max at all a>0 ⇒ 1 absolute min](Q208436.png)
$$\mathrm{It}'\mathrm{s}\:\mathrm{not}\:\mathrm{true}\:\mathrm{for}\:−\frac{\mathrm{e}}{\mathrm{2}}\leqslant{a}\leqslant\mathrm{0} \\ $$$${a}<−\frac{\mathrm{e}}{\mathrm{2}}\:\Rightarrow\:\mathrm{1}\:\mathrm{local}\:\mathrm{min}\:\mathrm{plus}\:\mathrm{1}\:\mathrm{local}\:\mathrm{max} \\ $$$${a}=−\frac{\mathrm{e}}{\mathrm{2}}\:\Rightarrow\:\mathrm{1}\:\mathrm{saddle}\:\mathrm{point}\:\left[\:_{\mathrm{horizontal}\:\mathrm{tangent}} ^{=\mathrm{1}\:\mathrm{point}\:\mathrm{with}\:\mathrm{a}} \right] \\ $$$$−\frac{\mathrm{e}}{\mathrm{2}}<{a}\leqslant\mathrm{0}\:\Rightarrow\:\mathrm{no}\:\mathrm{min}/\mathrm{max}\:\mathrm{at}\:\mathrm{all} \\ $$$${a}>\mathrm{0}\:\Rightarrow\:\mathrm{1}\:\mathrm{absolute}\:\mathrm{min} \\ $$
