Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 208282 by hardmath last updated on 10/Jun/24

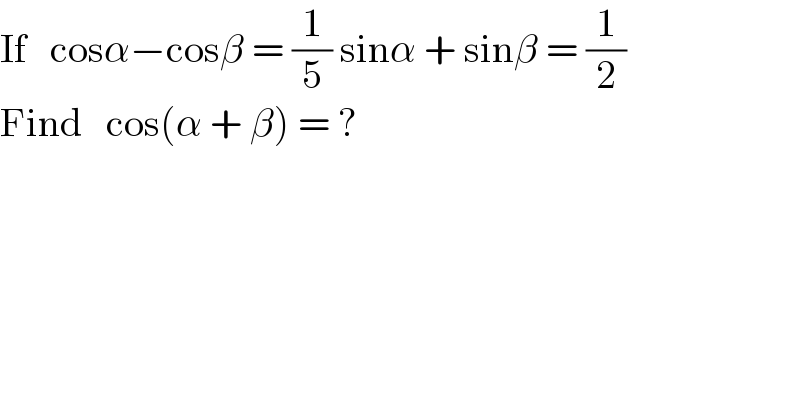
If cosα−cosβ = (1/5) sinα + sinβ = (1/2) Find cos(α + β) = ?

$$\mathrm{If}\:\:\:\mathrm{cos}\alpha−\mathrm{cos}\beta\:=\:\frac{\mathrm{1}}{\mathrm{5}}\:\mathrm{sin}\alpha\:+\:\mathrm{sin}\beta\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{Find}\:\:\:\mathrm{cos}\left(\alpha\:+\:\beta\right)\:=\:? \\ $$

Commented by mr W last updated on 12/Jun/24

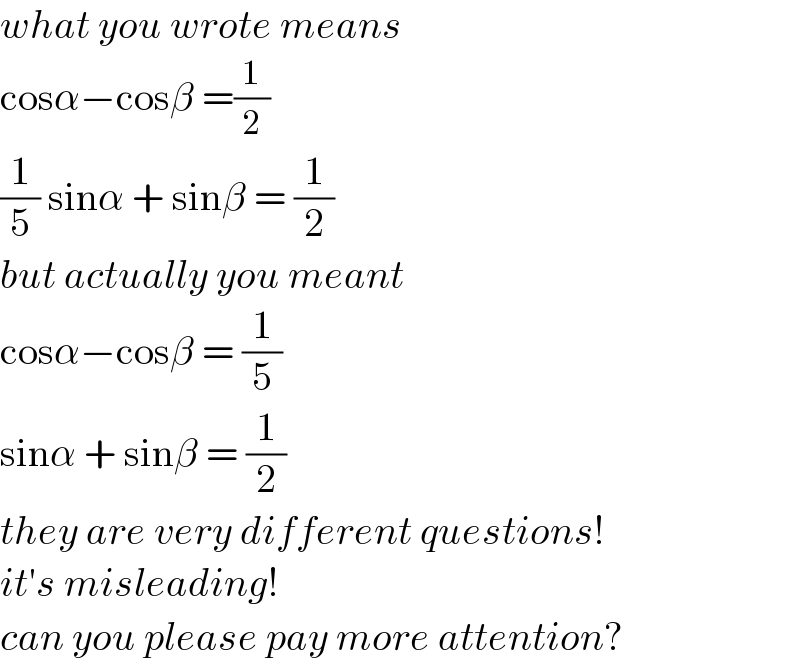
what you wrote means cosα−cosβ =(1/2) (1/5) sinα + sinβ = (1/2) but actually you meant cosα−cosβ = (1/5) sinα + sinβ = (1/2) they are very different questions! it′s misleading! can you please pay more attention?

$${what}\:{you}\:{wrote}\:{means} \\ $$$$\mathrm{cos}\alpha−\mathrm{cos}\beta\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}\:\mathrm{sin}\alpha\:+\:\mathrm{sin}\beta\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${but}\:{actually}\:{you}\:{meant} \\ $$$$\mathrm{cos}\alpha−\mathrm{cos}\beta\:=\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\mathrm{sin}\alpha\:+\:\mathrm{sin}\beta\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${they}\:{are}\:{very}\:{different}\:{questions}! \\ $$$${it}'{s}\:{misleading}! \\ $$$${can}\:{you}\:{please}\:{pay}\:{more}\:{attention}? \\ $$

Commented by Frix last updated on 10/Jun/24

I solved both versions but one gives no useable exact result, thus I think the other one was meant.

$$\mathrm{I}\:\mathrm{solved}\:\mathrm{both}\:\mathrm{versions}\:\mathrm{but}\:\mathrm{one}\:\mathrm{gives}\:\mathrm{no} \\ $$$$\mathrm{useable}\:\mathrm{exact}\:\mathrm{result},\:\mathrm{thus}\:\mathrm{I}\:\mathrm{think}\:\mathrm{the} \\ $$$$\mathrm{other}\:\mathrm{one}\:\mathrm{was}\:\mathrm{meant}. \\ $$

Answered by Frix last updated on 10/Jun/24

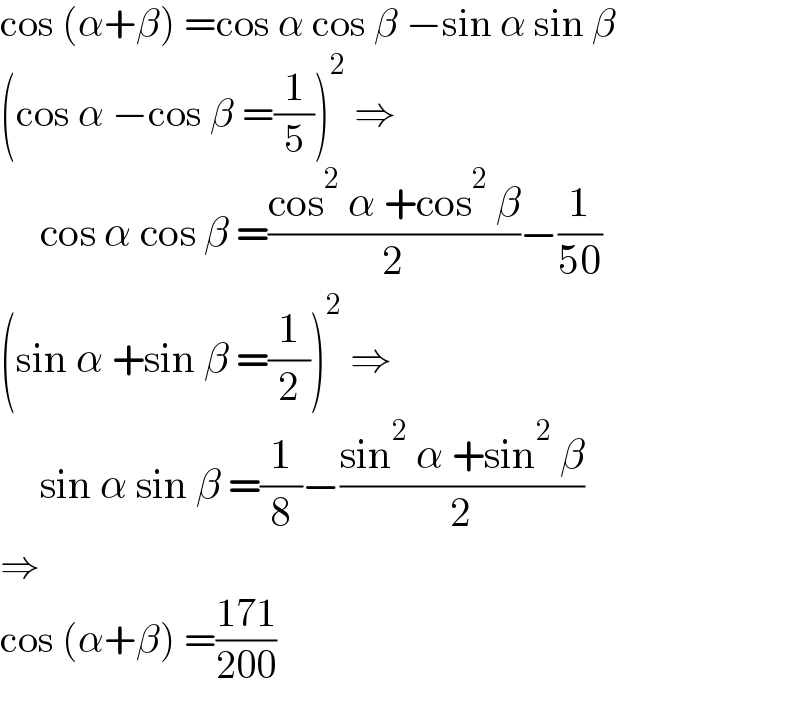
cos (α+β) =cos α cos β −sin α sin β (cos α −cos β =(1/5))^2 ⇒ cos α cos β =((cos^2 α +cos^2 β)/2)−(1/(50)) (sin α +sin β =(1/2))^2 ⇒ sin α sin β =(1/8)−((sin^2 α +sin^2 β)/2) ⇒ cos (α+β) =((171)/(200))

$$\mathrm{cos}\:\left(\alpha+\beta\right)\:=\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta\:−\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta \\ $$$$\left(\mathrm{cos}\:\alpha\:−\mathrm{cos}\:\beta\:=\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\:\:\:\:\:\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta\:=\frac{\mathrm{cos}^{\mathrm{2}} \:\alpha\:+\mathrm{cos}^{\mathrm{2}} \:\beta}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{50}} \\ $$$$\left(\mathrm{sin}\:\alpha\:+\mathrm{sin}\:\beta\:=\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\:\:\:\:\:\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta\:=\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{sin}^{\mathrm{2}} \:\alpha\:+\mathrm{sin}^{\mathrm{2}} \:\beta}{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\mathrm{cos}\:\left(\alpha+\beta\right)\:=\frac{\mathrm{171}}{\mathrm{200}} \\ $$

Commented by efronzo1 last updated on 10/Jun/24

cos α−cos β=(1/2)

$$\:\mathrm{cos}\:\alpha−\mathrm{cos}\:\beta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by hardmath last updated on 10/Jun/24

yes dear professor thank you

$$\mathrm{yes}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you} \\ $$

Commented by hardmath last updated on 10/Jun/24

answer: 171/200

$$\mathrm{answer}:\:\mathrm{171}/\mathrm{200} \\ $$

Commented by efronzo1 last updated on 10/Jun/24

$$\:\underbrace{\:} \\ $$

Commented by Frix last updated on 10/Jun/24

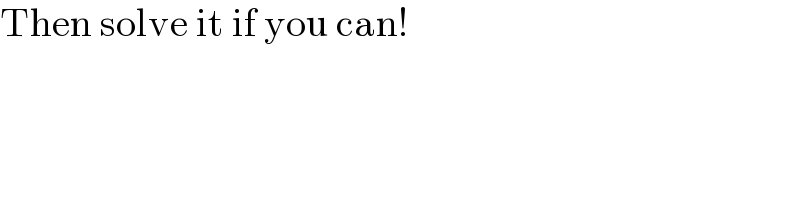
Then solve it if you can!

$$\mathrm{Then}\:\mathrm{solve}\:\mathrm{it}\:\mathrm{if}\:\mathrm{you}\:\mathrm{can}! \\ $$

Commented by efronzo1 last updated on 11/Jun/24

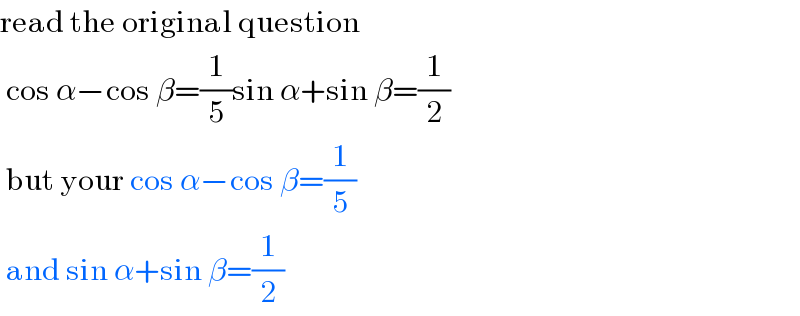
read the original question cos α−cos β=(1/5)sin α+sin β=(1/2) but your cos α−cos β=(1/5) and sin α+sin β=(1/2)

$$\mathrm{read}\:\mathrm{the}\:\mathrm{original}\:\mathrm{question} \\ $$$$\:\mathrm{cos}\:\alpha−\mathrm{cos}\:\beta=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{sin}\:\alpha+\mathrm{sin}\:\beta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\mathrm{but}\:\mathrm{your}\:\mathrm{cos}\:\alpha−\mathrm{cos}\:\beta=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\:\mathrm{and}\:\mathrm{sin}\:\alpha+\mathrm{sin}\:\beta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by mr W last updated on 11/Jun/24

the confusion was caused by hardmath sir through his misleading writing of the question.

$${the}\:{confusion}\:{was}\:{caused}\:{by}\: \\ $$$$\boldsymbol{{hardmath}}\:{sir}\:{through}\:{his}\: \\ $$$${misleading}\:{writing}\:{of}\:{the}\:{question}. \\ $$

Commented by Frix last updated on 11/Jun/24

@efronzo1: As I wrote before I also solved this one but it gives no useable exact result, we can only approximate it. So I decided that the other version with the "nice" result was the right one.

Terms of Service

Privacy Policy

Contact: info@tinkutara.com