Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 208149 by mnjuly1970 last updated on 06/Jun/24

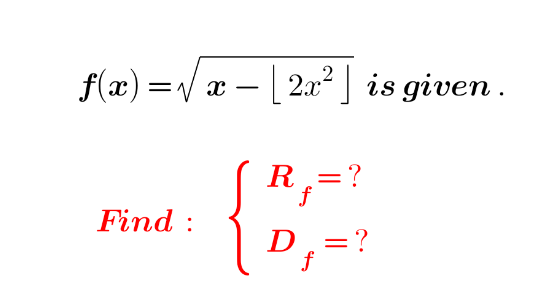
Answered by A5T last updated on 06/Jun/24

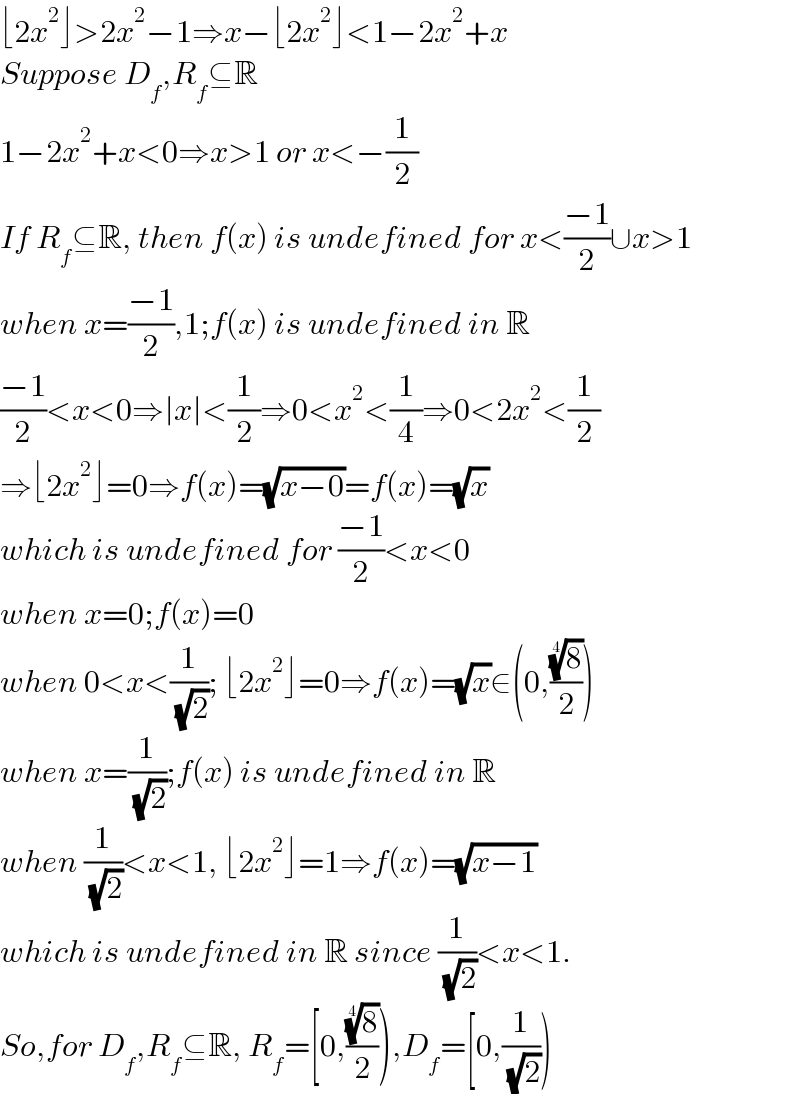
⌊2x^2 ⌋>2x^2 −1⇒x−⌊2x^2 ⌋<1−2x^2 +x Suppose D_f ,R_f ⊆R 1−2x^2 +x<0⇒x>1 or x<−(1/2) If R_f ⊆R, then f(x) is undefined for x<((−1)/2)∪x>1 when x=((−1)/2),1;f(x) is undefined in R ((−1)/2)<x<0⇒∣x∣<(1/2)⇒0<x^2 <(1/4)⇒0<2x^2 <(1/2) ⇒⌊2x^2 ⌋=0⇒f(x)=(√(x−0))=f(x)=(√x) which is undefined for ((−1)/2)<x<0 when x=0;f(x)=0 when 0<x<(1/( (√2))); ⌊2x^2 ⌋=0⇒f(x)=(√x)∈(0,((8)^(1/4) /2)) when x=(1/( (√2)));f(x) is undefined in R when (1/( (√2)))<x<1, ⌊2x^2 ⌋=1⇒f(x)=(√(x−1)) which is undefined in R since (1/( (√2)))<x<1. So,for D_f ,R_f ⊆R, R_f =[0,((8)^(1/4) /2)),D_f =[0,(1/( (√2))))

$$\lfloor\mathrm{2}{x}^{\mathrm{2}} \rfloor>\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}\Rightarrow{x}−\lfloor\mathrm{2}{x}^{\mathrm{2}} \rfloor<\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} +{x} \\ $$$${Suppose}\:{D}_{{f}} ,{R}_{{f}} \subseteq\mathbb{R} \\ $$$$\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} +{x}<\mathrm{0}\Rightarrow{x}>\mathrm{1}\:{or}\:{x}<−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${If}\:{R}_{{f}} \subseteq\mathbb{R},\:{then}\:{f}\left({x}\right)\:{is}\:{undefined}\:{for}\:{x}<\frac{−\mathrm{1}}{\mathrm{2}}\cup{x}>\mathrm{1} \\ $$$${when}\:{x}=\frac{−\mathrm{1}}{\mathrm{2}},\mathrm{1};{f}\left({x}\right)\:{is}\:{undefined}\:{in}\:\mathbb{R} \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}}<{x}<\mathrm{0}\Rightarrow\mid{x}\mid<\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{0}<{x}^{\mathrm{2}} <\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow\mathrm{0}<\mathrm{2}{x}^{\mathrm{2}} <\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\lfloor\mathrm{2}{x}^{\mathrm{2}} \rfloor=\mathrm{0}\Rightarrow{f}\left({x}\right)=\sqrt{{x}−\mathrm{0}}={f}\left({x}\right)=\sqrt{{x}} \\ $$$${which}\:{is}\:{undefined}\:{for}\:\frac{−\mathrm{1}}{\mathrm{2}}<{x}<\mathrm{0}\:\: \\ $$$${when}\:{x}=\mathrm{0};{f}\left({x}\right)=\mathrm{0} \\ $$$${when}\:\mathrm{0}<{x}<\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}};\:\lfloor\mathrm{2}{x}^{\mathrm{2}} \rfloor=\mathrm{0}\Rightarrow{f}\left({x}\right)=\sqrt{{x}}\in\left(\mathrm{0},\frac{\sqrt[{\mathrm{4}}]{\mathrm{8}}}{\mathrm{2}}\right) \\ $$$${when}\:{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}};{f}\left({x}\right)\:{is}\:{undefined}\:{in}\:\mathbb{R} \\ $$$${when}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}<{x}<\mathrm{1},\:\lfloor\mathrm{2}{x}^{\mathrm{2}} \rfloor=\mathrm{1}\Rightarrow{f}\left({x}\right)=\sqrt{{x}−\mathrm{1}} \\ $$$${which}\:{is}\:{undefined}\:{in}\:\mathbb{R}\:{since}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}<{x}<\mathrm{1}. \\ $$$${So},{for}\:{D}_{{f}} ,{R}_{{f}} \subseteq\mathbb{R},\:{R}_{{f}} =\left[\mathrm{0},\frac{\sqrt[{\mathrm{4}}]{\mathrm{8}}}{\mathrm{2}}\right),{D}_{{f}} =\left[\mathrm{0},\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right) \\ $$

Commented by mnjuly1970 last updated on 06/Jun/24

$$\: \\ $$

Commented by A5T last updated on 06/Jun/24

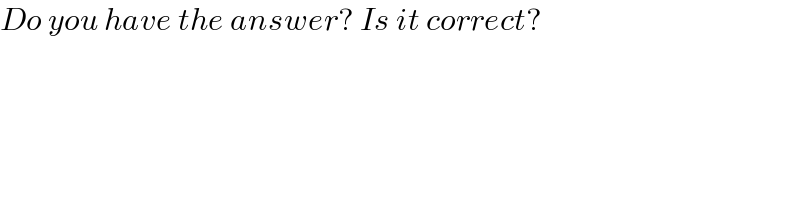
Do you have the answer? Is it correct?

$${Do}\:{you}\:{have}\:{the}\:{answer}?\:{Is}\:{it}\:{correct}? \\ $$

Commented by mnjuly1970 last updated on 07/Jun/24

yes sir A5T

$${yes}\:{sir}\:{A}\mathrm{5}{T} \\ $$

Answered by MM42 last updated on 06/Jun/24

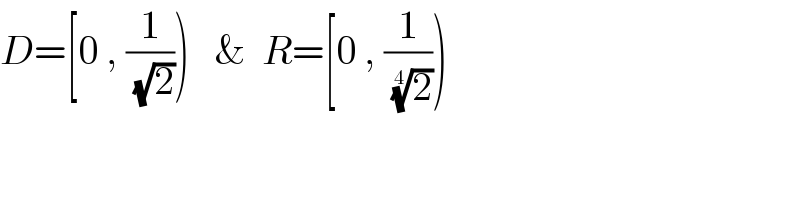
D=[0 , (1/( (√2)))) & R=[0 , (1/( (2)^(1/4) )))

$${D}=\left[\mathrm{0}\:,\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\:\:\:\&\:\:{R}=\left[\mathrm{0}\:,\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{\mathrm{2}}}\right) \\ $$$$ \\ $$$$ \\ $$

Commented by MM42 last updated on 06/Jun/24

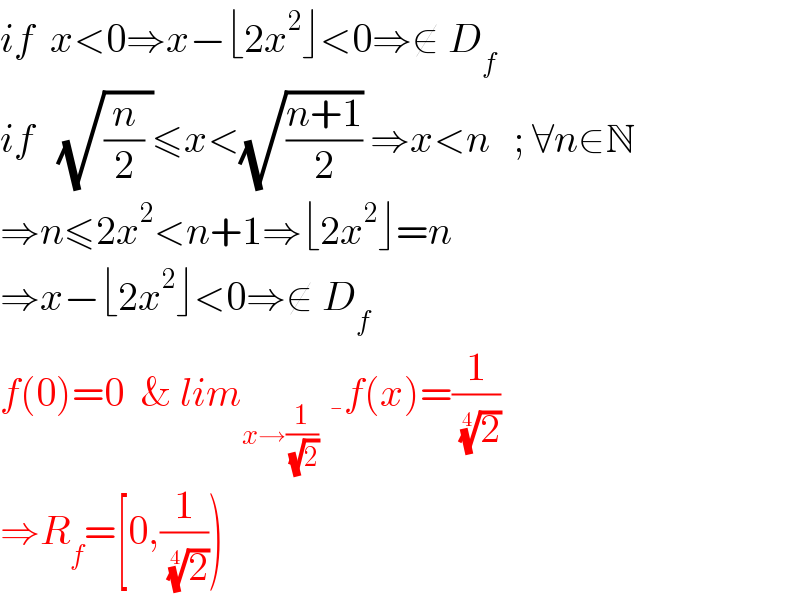
if x<0⇒x−⌊2x^2 ⌋<0⇒∉ D_f if (√((n/2) ))≤x<(√((n+1)/2)) ⇒x<n ; ∀n∈N ⇒n≤2x^2 <n+1⇒⌊2x^2 ⌋=n ⇒x−⌊2x^2 ⌋<0⇒∉ D_f f(0)=0 & lim_(x→(1/( (√2)))^ ) f(x)=(1/( (2)^(1/4) )) ⇒R_f =[0,(1/( (2)^(1/4) )))

$${if}\:\:{x}<\mathrm{0}\Rightarrow{x}−\lfloor\mathrm{2}{x}^{\mathrm{2}} \rfloor<\mathrm{0}\Rightarrow\notin\:{D}_{{f}} \\ $$$${if}\:\:\:\sqrt{\frac{{n}}{\mathrm{2}}\:}\leqslant{x}<\sqrt{\frac{{n}+\mathrm{1}}{\mathrm{2}}}\:\Rightarrow{x}<{n}\:\:\:;\:\forall{n}\in\mathbb{N} \\ $$$$\Rightarrow{n}\leqslant\mathrm{2}{x}^{\mathrm{2}} <{n}+\mathrm{1}\Rightarrow\lfloor\mathrm{2}{x}^{\mathrm{2}} \rfloor={n} \\ $$$$\Rightarrow{x}−\lfloor\mathrm{2}{x}^{\mathrm{2}} \rfloor<\mathrm{0}\Rightarrow\notin\:{D}_{{f}} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}\:\:\&\:{lim}_{{x}\rightarrow\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:^{} } {f}\left({x}\right)=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{\mathrm{2}}} \\ $$$$\Rightarrow{R}_{{f}} =\left[\mathrm{0},\frac{\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{\mathrm{2}}}\right) \\ $$

Answered by mnjuly1970 last updated on 07/Jun/24

x−⌊2x^2 ⌋≥0 ⇒ x ≥ ⌊ 2x^2 ⌋≥0 (★) −−−−−− ⌊ 2x^2 ⌋=k ⇒^(k∈Z^(≥0) ) k ≤ 2x^2 < k+1 from (★): x ≥ k ⇒^(x≥0) 2x^2 ≥ 2k^2 (★★) −−−−−− from(★),(★★)⇒^(★∩★★={}) : 2k^2 ≥ k+1 k ≥ 1 (■) complement of(■) is our purpose (★★★) k =0 ⇒ 0 ≤ 2x^2 < 1 ⇒ { ((D_f = 0≤x <(1/( (√2))))),(( ⌊2x^2 ⌋=0 ⇒ f(x)=(√x))) :} ⇒ { (( 0≤x <(1/( (√2))))),(( f(x)=(√x) ⇒ R_f = [0 , (1/( (2)^(1/4) )) ))) :}

$$\:\: \\ $$$$\:\:\:\:\:\:\:\:{x}−\lfloor\mathrm{2}{x}^{\mathrm{2}} \rfloor\geqslant\mathrm{0}\:\Rightarrow\:{x}\:\geqslant\:\lfloor\:\mathrm{2}{x}^{\mathrm{2}} \rfloor\geqslant\mathrm{0}\:\left(\bigstar\right) \\ $$$$\:\:\:\:\:\:\:−−−−−− \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\lfloor\:\mathrm{2}{x}^{\mathrm{2}} \rfloor={k}\:\overset{{k}\in\mathbb{Z}^{\geqslant\mathrm{0}} } {\Rightarrow}{k}\:\leqslant\:\mathrm{2}{x}^{\mathrm{2}} <\:{k}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:{from}\:\left(\bigstar\right):\:\:{x}\:\geqslant\:{k}\:\overset{{x}\geqslant\mathrm{0}} {\Rightarrow}\mathrm{2}{x}^{\mathrm{2}} \geqslant\:\mathrm{2}{k}^{\mathrm{2}} \left(\bigstar\bigstar\right) \\ $$$$\:\:\:\:\:\:−−−−−− \\ $$$$\:\:\:\:{from}\left(\bigstar\right),\left(\bigstar\bigstar\right)\overset{\bigstar\cap\bigstar\bigstar=\left\{\right\}} {\Rightarrow}\::\:\:\:\:\mathrm{2}{k}^{\mathrm{2}} \:\geqslant\:{k}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:{k}\:\geqslant\:\mathrm{1}\:\:\:\left(\blacksquare\right)\: \\ $$$$\:\:\:\:\:{complement}\:{of}\left(\blacksquare\right)\:{is}\:{our}\:{purpose}\:\:\left(\bigstar\bigstar\bigstar\right) \\ $$$$\:\:\:\:\:\:\:{k}\:=\mathrm{0}\:\Rightarrow\:\:\mathrm{0}\:\leqslant\:\mathrm{2}{x}^{\mathrm{2}} \:<\:\mathrm{1}\:\Rightarrow\:\begin{cases}{{D}_{{f}} =\:\mathrm{0}\leqslant{x}\:<\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}\\{\:\:\:\lfloor\mathrm{2}{x}^{\mathrm{2}} \rfloor=\mathrm{0}\:\Rightarrow\:{f}\left({x}\right)=\sqrt{{x}}}\end{cases}\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow\:\:\begin{cases}{\:\:\mathrm{0}\leqslant{x}\:<\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}\\{\:{f}\left({x}\right)=\sqrt{{x}}\:\Rightarrow\:{R}_{{f}} \:=\:\left[\mathrm{0}\:,\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{\mathrm{2}}}\:\right)}\end{cases} \\ $$$$ \\ $$$$\:\:\:\:\:\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com