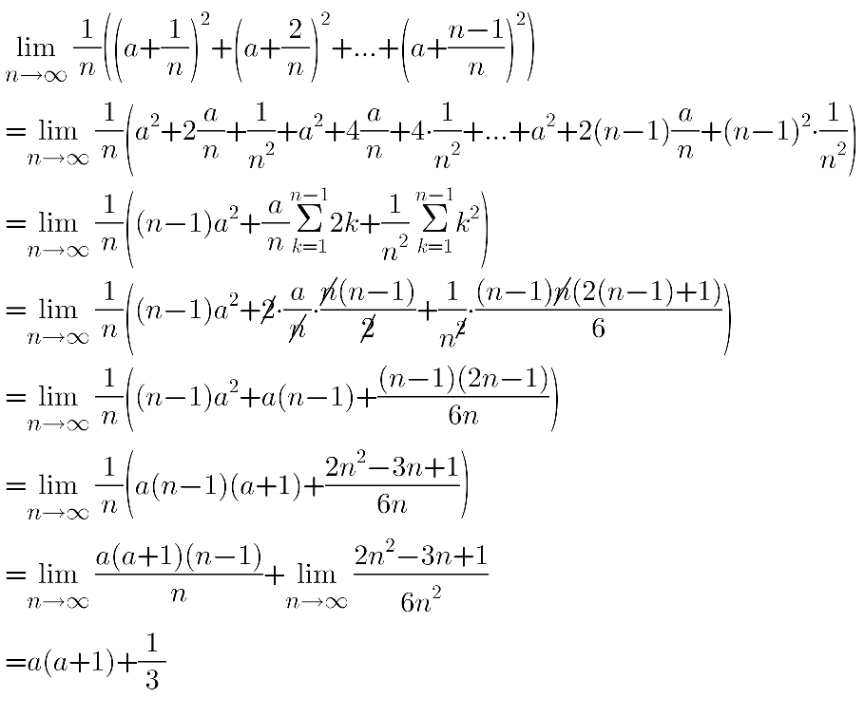Question Number 208093 by depressiveshrek last updated on 04/Jun/24
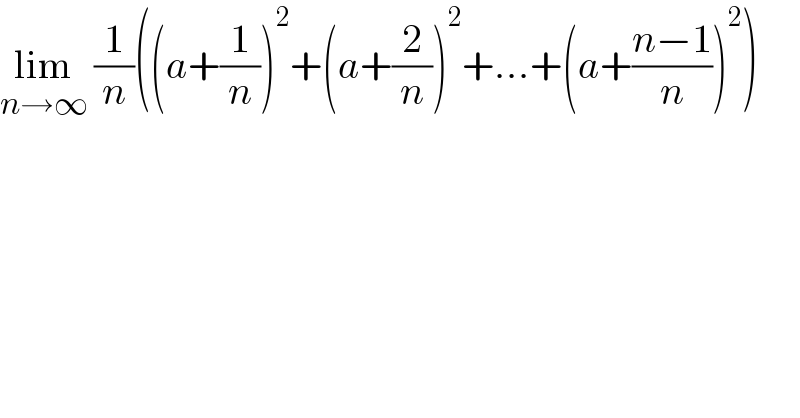
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{{n}}\left(\left({a}+\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} +\left({a}+\frac{\mathrm{2}}{{n}}\right)^{\mathrm{2}} +...+\left({a}+\frac{{n}−\mathrm{1}}{{n}}\right)^{\mathrm{2}} \right) \\ $$
Answered by MM42 last updated on 04/Jun/24
![=lim_(n→∞) (1/n)Σ_(i=1) ^(n−1) (a+(i/n))^2 =∫_0 ^1 (a+x)^2 dx=(1/3)(a+x)^3 ]_0 ^1 =(1/3)[(a+1)^3 −a^3 ] =(1/3)(3a^2 +3a+1) ✓](Q208094.png)
$$={lim}_{{n}\rightarrow\infty} \frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left({a}+\frac{{i}}{{n}}\right)^{\mathrm{2}} \\ $$$$\left.=\int_{\mathrm{0}} ^{\mathrm{1}} \left({a}+{x}\right)^{\mathrm{2}} {dx}=\frac{\mathrm{1}}{\mathrm{3}}\left({a}+{x}\right)^{\mathrm{3}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[\left({a}+\mathrm{1}\right)^{\mathrm{3}} −{a}^{\mathrm{3}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{3}{a}^{\mathrm{2}} +\mathrm{3}{a}+\mathrm{1}\right)\:\:\checkmark\: \\ $$
Commented by depressiveshrek last updated on 04/Jun/24

$$\mathrm{This}\:\mathrm{was}\:\mathrm{my}\:\mathrm{way}\:\mathrm{of}\:\mathrm{doing}\:\mathrm{it},\:\mathrm{sufficient} \\ $$$$\mathrm{for}\:\mathrm{a}\:\mathrm{calculus}\:\mathrm{1}\:\mathrm{course} \\ $$
Commented by depressiveshrek last updated on 04/Jun/24