
Question Number 207416 by efronzo1 last updated on 14/May/24

$$\:\:\: \\ $$
Answered by mr W last updated on 14/May/24
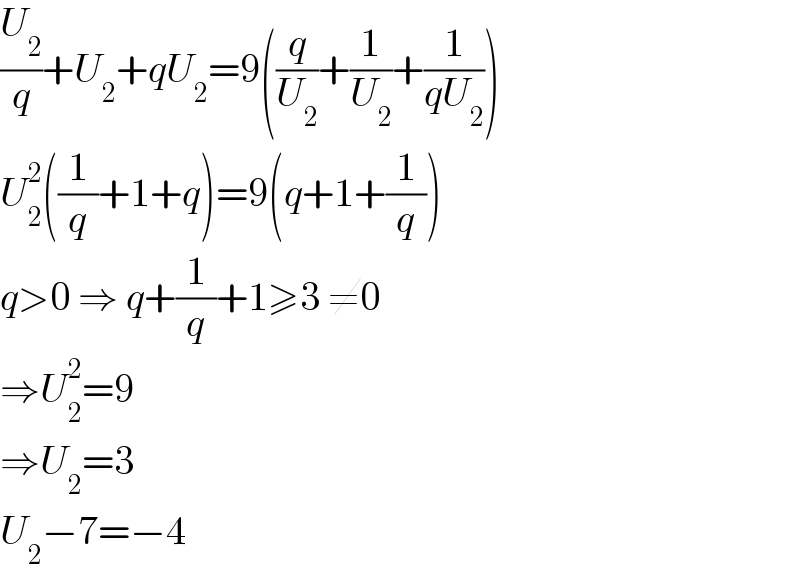
$$\frac{{U}_{\mathrm{2}} }{{q}}+{U}_{\mathrm{2}} +{qU}_{\mathrm{2}} =\mathrm{9}\left(\frac{{q}}{{U}_{\mathrm{2}} }+\frac{\mathrm{1}}{{U}_{\mathrm{2}} }+\frac{\mathrm{1}}{{qU}_{\mathrm{2}} }\right) \\ $$$${U}_{\mathrm{2}} ^{\mathrm{2}} \left(\frac{\mathrm{1}}{{q}}+\mathrm{1}+{q}\right)=\mathrm{9}\left({q}+\mathrm{1}+\frac{\mathrm{1}}{{q}}\right) \\ $$$${q}>\mathrm{0}\:\Rightarrow\:{q}+\frac{\mathrm{1}}{{q}}+\mathrm{1}\geqslant\mathrm{3}\:\neq\mathrm{0} \\ $$$$\Rightarrow{U}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{9} \\ $$$$\Rightarrow{U}_{\mathrm{2}} =\mathrm{3} \\ $$$${U}_{\mathrm{2}} −\mathrm{7}=−\mathrm{4} \\ $$
Answered by Rasheed.Sindhi last updated on 14/May/24
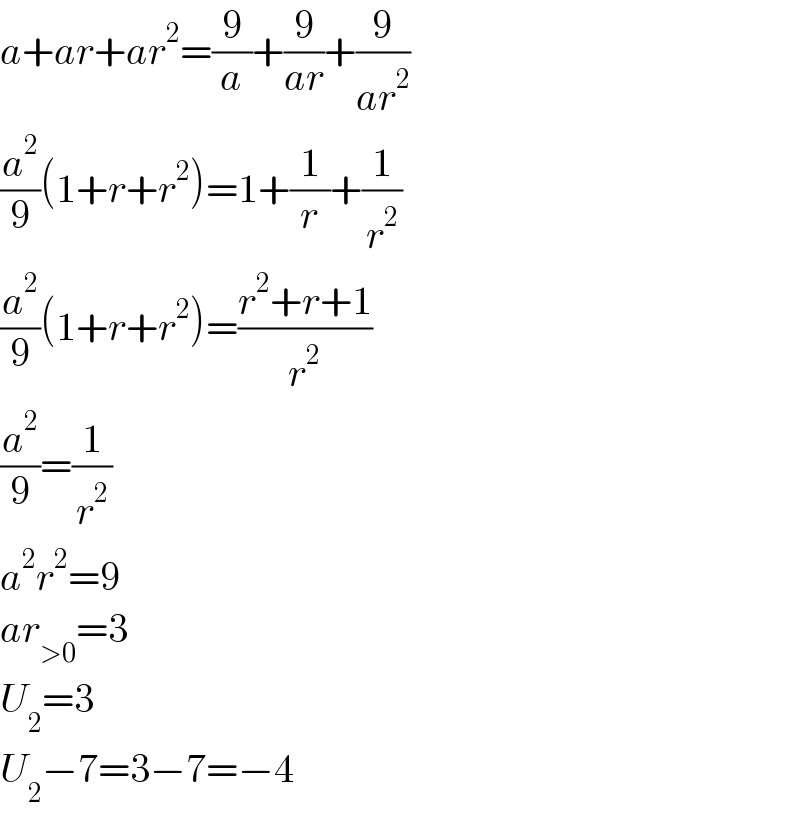
$${a}+{ar}+{ar}^{\mathrm{2}} =\frac{\mathrm{9}}{{a}}+\frac{\mathrm{9}}{{ar}}+\frac{\mathrm{9}}{{ar}^{\mathrm{2}} } \\ $$$$\frac{{a}^{\mathrm{2}} }{\mathrm{9}}\left(\mathrm{1}+{r}+{r}^{\mathrm{2}} \right)=\mathrm{1}+\frac{\mathrm{1}}{{r}}+\frac{\mathrm{1}}{{r}^{\mathrm{2}} } \\ $$$$\frac{{a}^{\mathrm{2}} }{\mathrm{9}}\left(\mathrm{1}+{r}+{r}^{\mathrm{2}} \right)=\frac{{r}^{\mathrm{2}} +{r}+\mathrm{1}}{{r}^{\mathrm{2}} } \\ $$$$\frac{{a}^{\mathrm{2}} }{\mathrm{9}}=\frac{\mathrm{1}}{{r}^{\mathrm{2}} } \\ $$$${a}^{\mathrm{2}} {r}^{\mathrm{2}} =\mathrm{9} \\ $$$${ar}_{>\mathrm{0}} =\mathrm{3} \\ $$$${U}_{\mathrm{2}} =\mathrm{3} \\ $$$${U}_{\mathrm{2}} −\mathrm{7}=\mathrm{3}−\mathrm{7}=−\mathrm{4} \\ $$
