
Question Number 207394 by hardmath last updated on 13/May/24
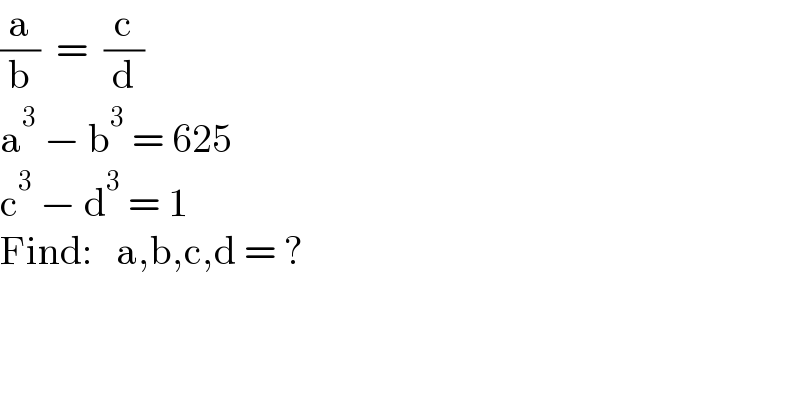
$$\frac{\mathrm{a}}{\mathrm{b}}\:\:=\:\:\frac{\mathrm{c}}{\mathrm{d}} \\ $$$$\mathrm{a}^{\mathrm{3}} \:−\:\mathrm{b}^{\mathrm{3}} \:=\:\mathrm{625} \\ $$$$\mathrm{c}^{\mathrm{3}} \:−\:\mathrm{d}^{\mathrm{3}} \:=\:\mathrm{1} \\ $$$$\mathrm{Find}:\:\:\:\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\:=\:? \\ $$
Answered by mr W last updated on 13/May/24
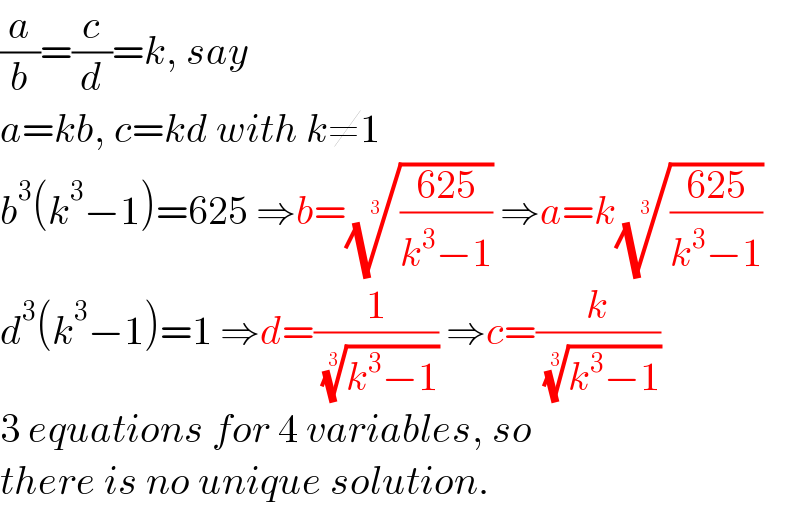
$$\frac{{a}}{{b}}=\frac{{c}}{{d}}={k},\:{say} \\ $$$${a}={kb},\:{c}={kd}\:{with}\:{k}\neq\mathrm{1} \\ $$$${b}^{\mathrm{3}} \left({k}^{\mathrm{3}} −\mathrm{1}\right)=\mathrm{625}\:\Rightarrow{b}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{625}}{{k}^{\mathrm{3}} −\mathrm{1}}}\:\Rightarrow{a}={k}\sqrt[{\mathrm{3}}]{\frac{\mathrm{625}}{{k}^{\mathrm{3}} −\mathrm{1}}} \\ $$$${d}^{\mathrm{3}} \left({k}^{\mathrm{3}} −\mathrm{1}\right)=\mathrm{1}\:\Rightarrow{d}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{k}^{\mathrm{3}} −\mathrm{1}}}\:\Rightarrow{c}=\frac{{k}}{\:\sqrt[{\mathrm{3}}]{{k}^{\mathrm{3}} −\mathrm{1}}} \\ $$$$\mathrm{3}\:{equations}\:{for}\:\mathrm{4}\:{variables},\:{so} \\ $$$${there}\:{is}\:{no}\:{unique}\:{solution}. \\ $$
