
Question Number 207205 by hardmath last updated on 09/May/24
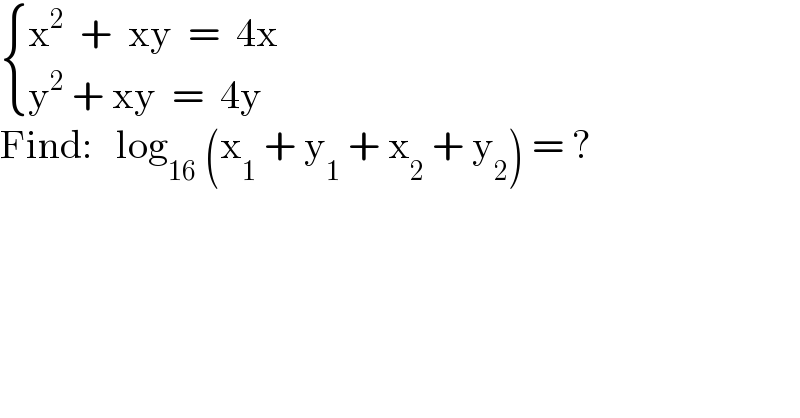
$$\begin{cases}{\mathrm{x}^{\mathrm{2}} \:\:+\:\:\mathrm{xy}\:\:=\:\:\mathrm{4x}}\\{\mathrm{y}^{\mathrm{2}} \:+\:\mathrm{xy}\:\:=\:\:\mathrm{4y}}\end{cases} \\ $$$$\mathrm{Find}:\:\:\:\mathrm{log}_{\mathrm{16}} \:\left(\mathrm{x}_{\mathrm{1}} \:+\:\mathrm{y}_{\mathrm{1}} \:+\:\mathrm{x}_{\mathrm{2}} \:+\:\mathrm{y}_{\mathrm{2}} \right)\:=\:? \\ $$
Answered by A5T last updated on 09/May/24
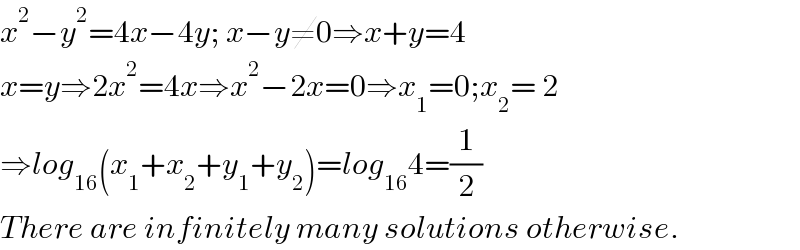
$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{4}{x}−\mathrm{4}{y};\:{x}−{y}\neq\mathrm{0}\Rightarrow{x}+{y}=\mathrm{4} \\ $$$${x}={y}\Rightarrow\mathrm{2}{x}^{\mathrm{2}} =\mathrm{4}{x}\Rightarrow{x}^{\mathrm{2}} −\mathrm{2}{x}=\mathrm{0}\Rightarrow{x}_{\mathrm{1}} =\mathrm{0};{x}_{\mathrm{2}} =\:\mathrm{2} \\ $$$$\Rightarrow{log}_{\mathrm{16}} \left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{y}_{\mathrm{1}} +{y}_{\mathrm{2}} \right)={log}_{\mathrm{16}} \mathrm{4}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${There}\:{are}\:{infinitely}\:{many}\:{solutions}\:{otherwise}. \\ $$
Commented by hardmath last updated on 09/May/24
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor} \\ $$
