
Question Number 206861 by MrGHK last updated on 28/Apr/24
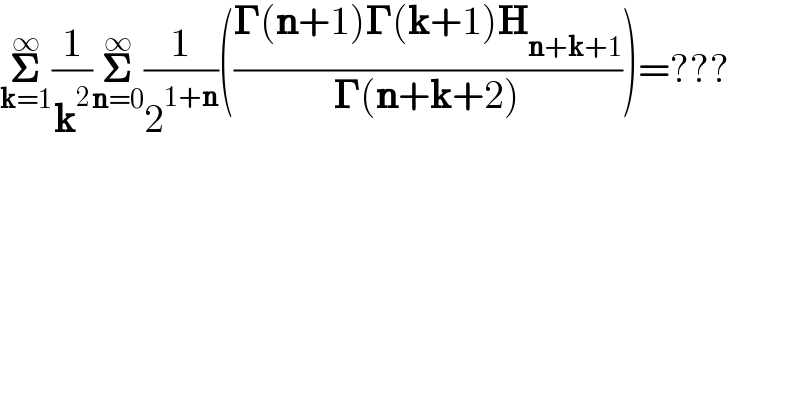
$$\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\boldsymbol{\sum}}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{k}}^{\mathrm{2}} }\underset{\boldsymbol{\mathrm{n}}=\mathrm{0}} {\overset{\infty} {\boldsymbol{\sum}}}\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}+\boldsymbol{\mathrm{n}}} }\left(\frac{\boldsymbol{\Gamma}\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)\boldsymbol{\Gamma}\left(\boldsymbol{\mathrm{k}}+\mathrm{1}\right)\boldsymbol{\mathrm{H}}_{\boldsymbol{\mathrm{n}}+\boldsymbol{\mathrm{k}}+\mathrm{1}} }{\boldsymbol{\Gamma}\left(\boldsymbol{\mathrm{n}}+\boldsymbol{\mathrm{k}}+\mathrm{2}\right)}\right)=??? \\ $$
