Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 206833 by BaliramKumar last updated on 27/Apr/24

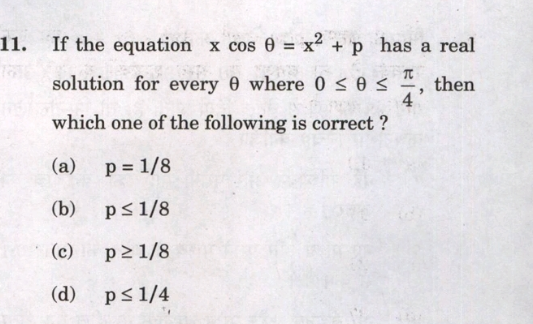
Answered by MATHEMATICSAM last updated on 27/Apr/24

If 0 ≤ θ ≤ (π/4) then (1/( (√2))) ≤ cosθ ≤ 1 Or, (1/2) ≤ cos^2 θ ≤ 1 xcosθ = x^2 + p ⇒ x^2 − xcosθ + p = 0 This equation has real solution for every θ where 0 ≤ θ ≤ (π/4) . So the discriminant of the equation cos^2 θ − 4p ≥ 0 ⇒ 4p ≤ cos^2 θ ≤ 1 ⇒ 4p ≤ 1 ⇒ p ≤ (1/4) Hence ans is option (d).

$$\mathrm{If}\:\mathrm{0}\:\leq\:\theta\:\leq\:\frac{\pi}{\mathrm{4}}\:\mathrm{then}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\leq\:\mathrm{cos}\theta\:\leq\:\mathrm{1}\: \\ $$$$\mathrm{Or},\:\frac{\mathrm{1}}{\mathrm{2}}\:\leq\:\mathrm{cos}^{\mathrm{2}} \theta\:\leq\:\mathrm{1} \\ $$$${x}\mathrm{cos}\theta\:=\:{x}^{\mathrm{2}} \:+\:{p} \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} \:−\:{x}\mathrm{cos}\theta\:+\:{p}\:=\:\mathrm{0} \\ $$$$\mathrm{This}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{for} \\ $$$$\mathrm{every}\:\theta\:\mathrm{where}\:\mathrm{0}\:\leq\:\theta\:\leq\:\frac{\pi}{\mathrm{4}}\:. \\ $$$$\mathrm{So}\:\mathrm{the}\:\mathrm{discriminant}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{cos}^{\mathrm{2}} \theta\:−\:\mathrm{4}{p}\:\geq\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{4}{p}\:\leq\:\mathrm{cos}^{\mathrm{2}} \theta\:\leq\:\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{4}{p}\:\leq\:\mathrm{1} \\ $$$$\Rightarrow\:{p}\:\leq\:\frac{\mathrm{1}}{\mathrm{4}}\:\: \\ $$$$\mathrm{Hence}\:\mathrm{ans}\:\mathrm{is}\:\mathrm{option}\:\left(\mathrm{d}\right). \\ $$

Commented by A5T last updated on 27/Apr/24

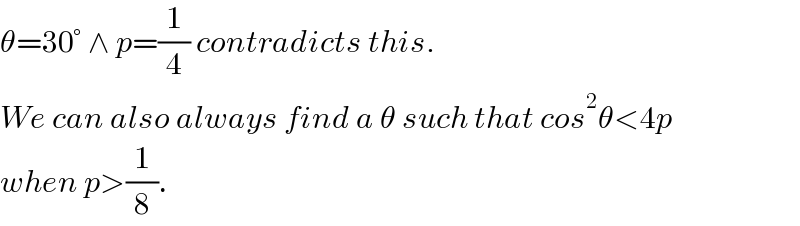
θ=30° ∧ p=(1/4) contradicts this. We can also always find a θ such that cos^2 θ<4p when p>(1/8).

$$\theta=\mathrm{30}°\:\wedge\:{p}=\frac{\mathrm{1}}{\mathrm{4}}\:{contradicts}\:{this}. \\ $$$${We}\:{can}\:{also}\:{always}\:{find}\:{a}\:\theta\:{such}\:{that}\:{cos}^{\mathrm{2}} \theta<\mathrm{4}{p} \\ $$$${when}\:{p}>\frac{\mathrm{1}}{\mathrm{8}}. \\ $$

Commented by MATHEMATICSAM last updated on 27/Apr/24

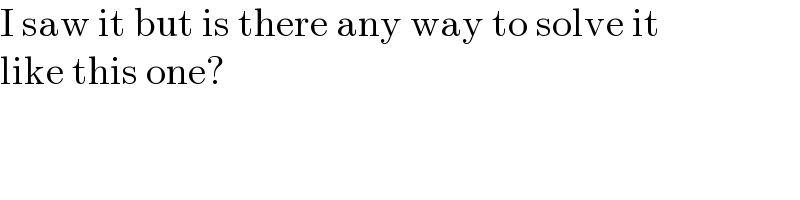
I saw it but is there any way to solve it like this one?

$$\mathrm{I}\:\mathrm{saw}\:\mathrm{it}\:\mathrm{but}\:\mathrm{is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{way}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{it} \\ $$$$\mathrm{like}\:\mathrm{this}\:\mathrm{one}? \\ $$

Commented by A5T last updated on 27/Apr/24

The problem with this is that from this chain 4p≤^? cos^2 θ≤1; we cannot conclude that 4p≤1 since we have not actually shown when 4p≤cos^2 θ and it is just a condition for the necessary pairs (p,θ). So, 4p must not exceed the minimum bound for cos^2 θ which is (1/2). Otherwise,we can always find θ such that (1/2)<cos^2 θ<4p, which contradicts the condition 4p≤cos^2 θ.

$${The}\:{problem}\:{with}\:{this}\:{is}\:{that}\:{from}\:{this}\:{chain} \\ $$$$\mathrm{4}{p}\overset{?} {\leqslant}{cos}^{\mathrm{2}} \theta\leqslant\mathrm{1};\:{we}\:{cannot}\:{conclude}\:{that}\:\mathrm{4}{p}\leqslant\mathrm{1} \\ $$$${since}\:{we}\:{have}\:{not}\:{actually}\:{shown}\:{when}\: \\ $$$$\mathrm{4}{p}\leqslant{cos}^{\mathrm{2}} \theta\:{and}\:{it}\:{is}\:{just}\:{a}\:{condition}\:{for}\:{the} \\ $$$${necessary}\:{pairs}\:\left({p},\theta\right). \\ $$$$ \\ $$$${So},\:\mathrm{4}{p}\:{must}\:{not}\:{exceed}\:{the}\:{minimum}\:{bound}\:{for} \\ $$$${cos}^{\mathrm{2}} \theta\:{which}\:{is}\:\frac{\mathrm{1}}{\mathrm{2}}.\:{Otherwise},{we}\:{can}\:{always} \\ $$$${find}\:\theta\:{such}\:{that}\:\frac{\mathrm{1}}{\mathrm{2}}<{cos}^{\mathrm{2}} \theta<\mathrm{4}{p},\:{which}\:{contradicts} \\ $$$${the}\:{condition}\:\mathrm{4}{p}\leqslant{cos}^{\mathrm{2}} \theta. \\ $$

Commented by MATHEMATICSAM last updated on 27/Apr/24

Hmm this is actually right.

$$\mathrm{Hmm}\:\mathrm{this}\:\mathrm{is}\:\mathrm{actually}\:\mathrm{right}. \\ $$

Answered by A5T last updated on 27/Apr/24

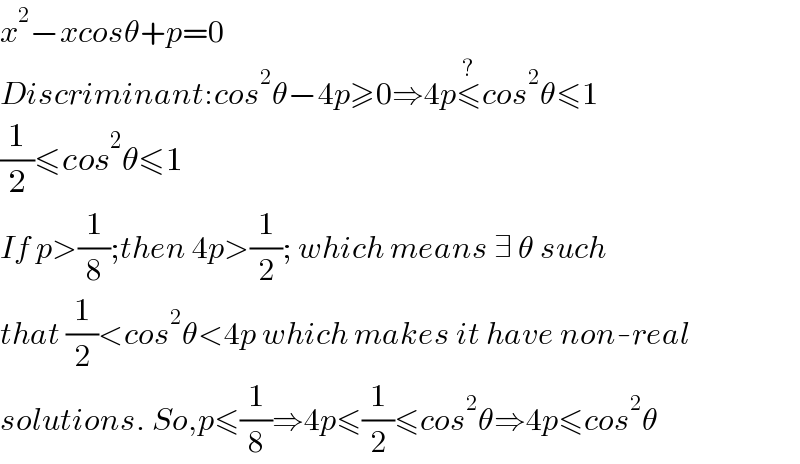
x^2 −xcosθ+p=0 Discriminant:cos^2 θ−4p≥0⇒4p≤^? cos^2 θ≤1 (1/2)≤cos^2 θ≤1 If p>(1/8);then 4p>(1/2); which means ∃ θ such that (1/2)<cos^2 θ<4p which makes it have non-real solutions. So,p≤(1/8)⇒4p≤(1/2)≤cos^2 θ⇒4p≤cos^2 θ

$${x}^{\mathrm{2}} −{xcos}\theta+{p}=\mathrm{0} \\ $$$${Discriminant}:{cos}^{\mathrm{2}} \theta−\mathrm{4}{p}\geqslant\mathrm{0}\Rightarrow\mathrm{4}{p}\overset{?} {\leqslant}{cos}^{\mathrm{2}} \theta\leqslant\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\leqslant{cos}^{\mathrm{2}} \theta\leqslant\mathrm{1} \\ $$$${If}\:{p}>\frac{\mathrm{1}}{\mathrm{8}};{then}\:\mathrm{4}{p}>\frac{\mathrm{1}}{\mathrm{2}};\:{which}\:{means}\:\exists\:\theta\:{such} \\ $$$${that}\:\frac{\mathrm{1}}{\mathrm{2}}<{cos}^{\mathrm{2}} \theta<\mathrm{4}{p}\:{which}\:{makes}\:{it}\:{have}\:{non}-{real} \\ $$$${solutions}.\:{So},{p}\leqslant\frac{\mathrm{1}}{\mathrm{8}}\Rightarrow\mathrm{4}{p}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\leqslant{cos}^{\mathrm{2}} \theta\Rightarrow\mathrm{4}{p}\leqslant{cos}^{\mathrm{2}} \theta \\ $$

Commented by BaliramKumar last updated on 27/Apr/24

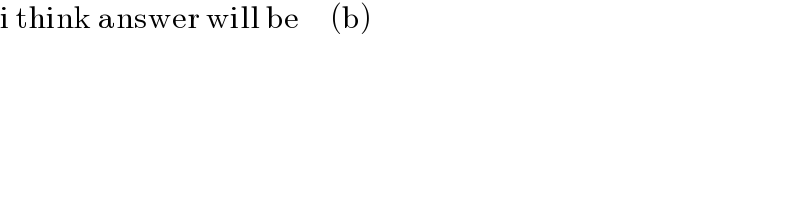
i think answer will be (b)

$$\mathrm{i}\:\mathrm{think}\:\mathrm{answer}\:\mathrm{will}\:\mathrm{be}\:\:\:\:\:\left(\mathrm{b}\right) \\ $$

Commented by A5T last updated on 27/Apr/24

How?

$${How}? \\ $$

Commented by BaliramKumar last updated on 27/Apr/24

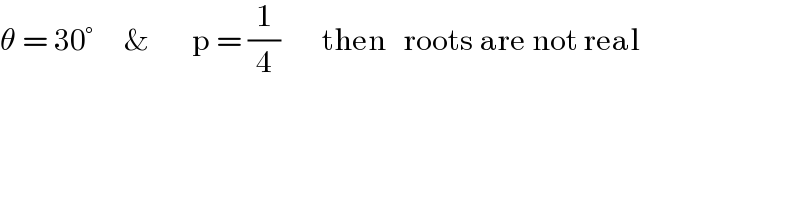
θ = 30° & p = (1/4) then roots are not real

$$\theta\:=\:\mathrm{30}°\:\:\:\:\:\&\:\:\:\:\:\:\:\mathrm{p}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:\:\:\mathrm{then}\:\:\:\mathrm{roots}\:\mathrm{are}\:\mathrm{not}\:\mathrm{real}\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Commented by A5T last updated on 27/Apr/24

Yea.

$${Yea}. \\ $$

Answered by Frix last updated on 27/Apr/24

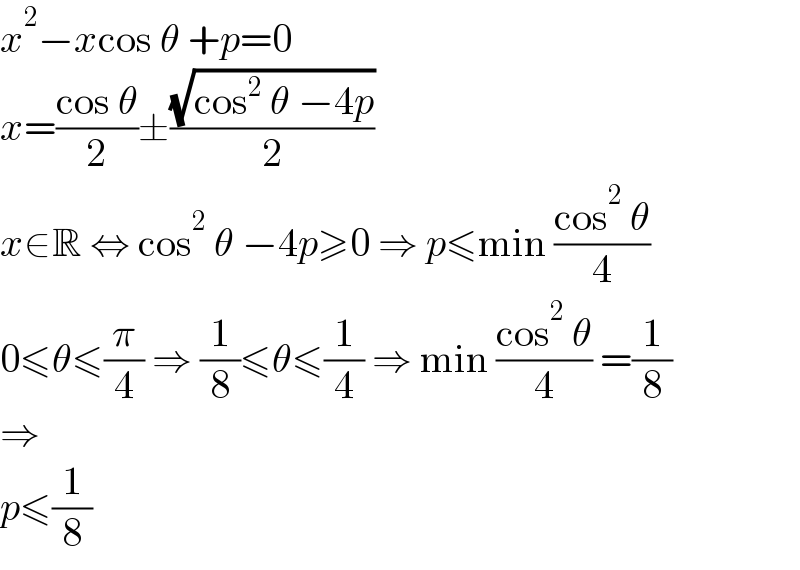
x^2 −xcos θ +p=0 x=((cos θ)/2)±((√(cos^2 θ −4p))/2) x∈R ⇔ cos^2 θ −4p≥0 ⇒ p≤min ((cos^2 θ)/4) 0≤θ≤(π/4) ⇒ (1/8)≤θ≤(1/4) ⇒ min ((cos^2 θ)/4) =(1/8) ⇒ p≤(1/8)

$${x}^{\mathrm{2}} −{x}\mathrm{cos}\:\theta\:+{p}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{cos}\:\theta}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{cos}^{\mathrm{2}} \:\theta\:−\mathrm{4}{p}}}{\mathrm{2}} \\ $$$${x}\in\mathbb{R}\:\Leftrightarrow\:\mathrm{cos}^{\mathrm{2}} \:\theta\:−\mathrm{4}{p}\geqslant\mathrm{0}\:\Rightarrow\:{p}\leqslant\mathrm{min}\:\frac{\mathrm{cos}^{\mathrm{2}} \:\theta}{\mathrm{4}} \\ $$$$\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{4}}\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{8}}\leqslant\theta\leqslant\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:\mathrm{min}\:\frac{\mathrm{cos}^{\mathrm{2}} \:\theta}{\mathrm{4}}\:=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\Rightarrow \\ $$$${p}\leqslant\frac{\mathrm{1}}{\mathrm{8}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com