
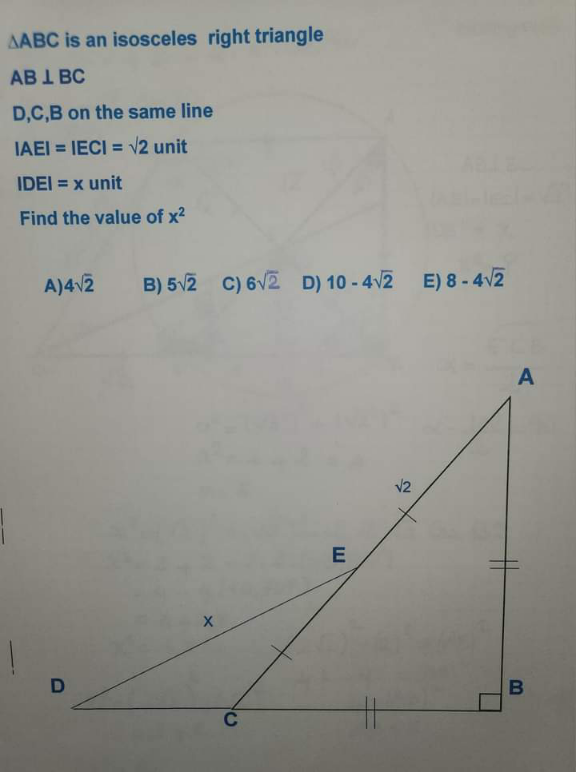
Question Number 205596 by cortano12 last updated on 25/Mar/24
Commented by A5T last updated on 25/Mar/24
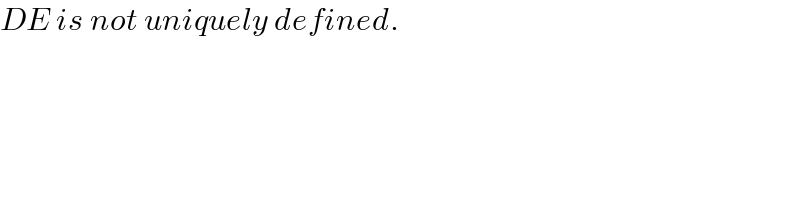
$${DE}\:{is}\:{not}\:{uniquely}\:{defined}. \\ $$
Answered by TheHoneyCat last updated on 31/Mar/24
![As pointed out by A5T this question is missing something to be solvable. To be more explicit, you are lacking a constraint on D. D is currently free to be anywhere on the line, so x can take any value from +∞ (if you send D to infinity) to 1 (which is the minial value you can get by putting D in the middle of [C,B].) So the smartass answer is [1,+∞[ but in all seriousness you are missing a line in your exercise somewhere...](Q205848.png)
$$\mathrm{As}\:\mathrm{pointed}\:\mathrm{out}\:\mathrm{by}\:{A}\mathrm{5}{T}\:\mathrm{this}\:\mathrm{question}\:\mathrm{is}\:\mathrm{missing} \\ $$$$\mathrm{something}\:\mathrm{to}\:\mathrm{be}\:\mathrm{solvable}. \\ $$$$ \\ $$$$\mathrm{To}\:\mathrm{be}\:\mathrm{more}\:\mathrm{explicit},\:\mathrm{you}\:\mathrm{are}\:\mathrm{lacking}\:\mathrm{a} \\ $$$$\mathrm{constraint}\:\mathrm{on}\:{D}.\:{D}\:\mathrm{is}\:\mathrm{currently}\:\mathrm{free}\:\mathrm{to} \\ $$$$\mathrm{be}\:\mathrm{anywhere}\:\mathrm{on}\:\mathrm{the}\:\mathrm{line},\:\mathrm{so}\:{x}\:\mathrm{can}\:\mathrm{take}\:\mathrm{any} \\ $$$$\mathrm{value}\:\mathrm{from}\:+\infty\:\left(\mathrm{if}\:\mathrm{you}\:\mathrm{send}\:{D}\:\mathrm{to}\:\mathrm{infinity}\right) \\ $$$$\mathrm{to}\:\mathrm{1}\:\left(\mathrm{which}\:\mathrm{is}\:\mathrm{the}\:\mathrm{minial}\:\mathrm{value}\:\mathrm{you}\:\mathrm{can}\:\mathrm{get}\right. \\ $$$$\left.\mathrm{by}\:\mathrm{putting}\:{D}\:\mathrm{in}\:\mathrm{the}\:\mathrm{middle}\:\mathrm{of}\:\left[{C},{B}\right].\right) \\ $$$$ \\ $$$$\mathrm{So}\:\mathrm{the}\:\mathrm{smartass}\:\mathrm{answer}\:\mathrm{is}\:\left[\mathrm{1},+\infty\left[\right.\right. \\ $$$$\mathrm{but}\:\mathrm{in}\:\mathrm{all}\:\mathrm{seriousness}\:\mathrm{you}\:\mathrm{are}\:\mathrm{missing}\:\mathrm{a}\:\mathrm{line} \\ $$$$\mathrm{in}\:\mathrm{your}\:\mathrm{exercise}\:\mathrm{somewhere}... \\ $$
Commented by A5T last updated on 31/Mar/24

$${The}\:{shortest}\:{distance}\:{from}\:{a}\:{point},{say}\:{E},{to}\:{a} \\ $$$${line},{say}\:{BD},\:{is}\:{the}\:{length}\:{of}\:{the}\:{perpendicular} \\ $$$${from}\:{E}\:{to}\:{BD}.\:{So},{to}\:{find}\:{the}\:{shortest}\:{distance}, \\ $$$${let}\:{the}\:{perpendicular}\:{from}\:{E}\:{to}\:{BD}\:{meet}\:{BD} \\ $$$${at}\:{F}.\:{Then},\:\frac{\mathrm{1}}{\mathrm{2}}=\frac{{EF}}{\mathrm{1}}\left({similar}\:\bigtriangleup\right)\Rightarrow{EF}=\frac{\mathrm{1}}{\mathrm{2}}. \\ $$
Commented by TheHoneyCat last updated on 31/Mar/24
Oh yeah, my bad ��. Thanks
