Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 205588 by cortano12 last updated on 25/Mar/24

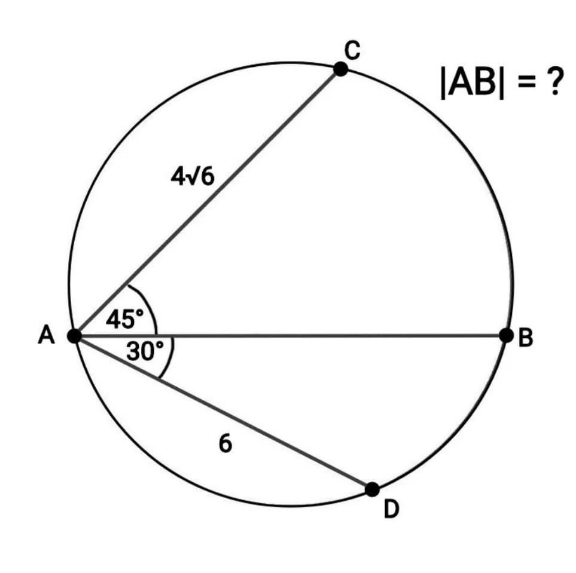
Answered by A5T last updated on 25/Mar/24

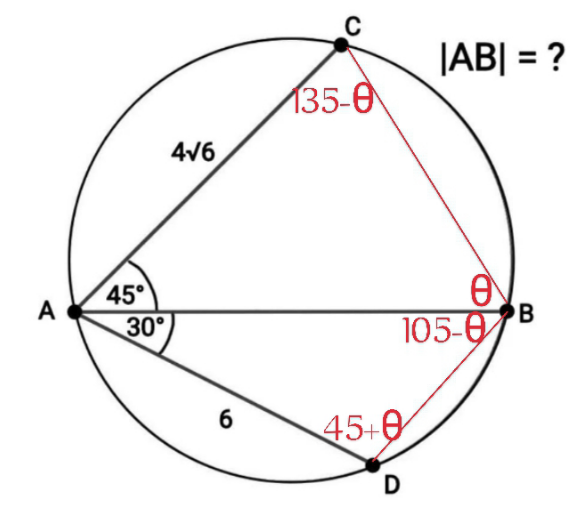
Commented by A5T last updated on 25/Mar/24

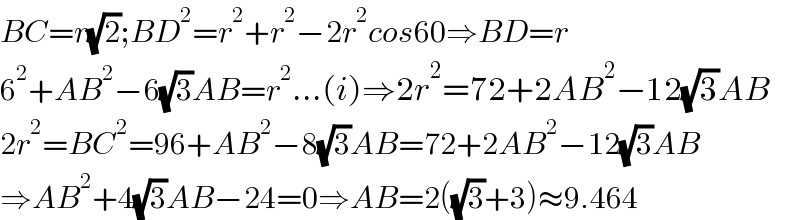
BC=r(√2);BD^2 =r^2 +r^2 −2r^2 cos60⇒BD=r 6^2 +AB^2 −6(√3)AB=r^2 ...(i)⇒2r^2 =72+2AB^2 −12(√3)AB 2r^2 =BC^2 =96+AB^2 −8(√3)AB=72+2AB^2 −12(√3)AB ⇒AB^2 +4(√3)AB−24=0⇒AB=2((√3)+3)≈9.464

$${BC}={r}\sqrt{\mathrm{2}};{BD}^{\mathrm{2}} ={r}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{r}^{\mathrm{2}} {cos}\mathrm{60}\Rightarrow{BD}={r} \\ $$$$\mathrm{6}^{\mathrm{2}} +{AB}^{\mathrm{2}} −\mathrm{6}\sqrt{\mathrm{3}}{AB}={r}^{\mathrm{2}} ...\left({i}\right)\Rightarrow\mathrm{2}{r}^{\mathrm{2}} =\mathrm{72}+\mathrm{2}{AB}^{\mathrm{2}} −\mathrm{12}\sqrt{\mathrm{3}}{AB} \\ $$$$\mathrm{2}{r}^{\mathrm{2}} ={BC}^{\mathrm{2}} =\mathrm{96}+{AB}^{\mathrm{2}} −\mathrm{8}\sqrt{\mathrm{3}}{AB}=\mathrm{72}+\mathrm{2}{AB}^{\mathrm{2}} −\mathrm{12}\sqrt{\mathrm{3}}{AB} \\ $$$$\Rightarrow{AB}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}{AB}−\mathrm{24}=\mathrm{0}\Rightarrow{AB}=\mathrm{2}\left(\sqrt{\mathrm{3}}+\mathrm{3}\right)\approx\mathrm{9}.\mathrm{464} \\ $$

Answered by mr W last updated on 25/Mar/24

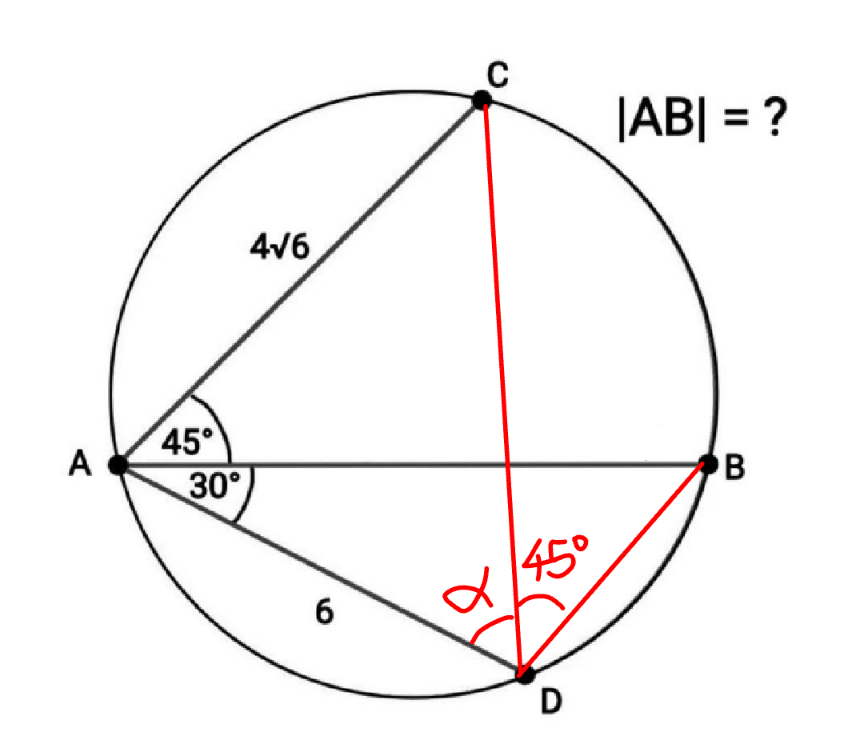
Commented by mr W last updated on 25/Mar/24

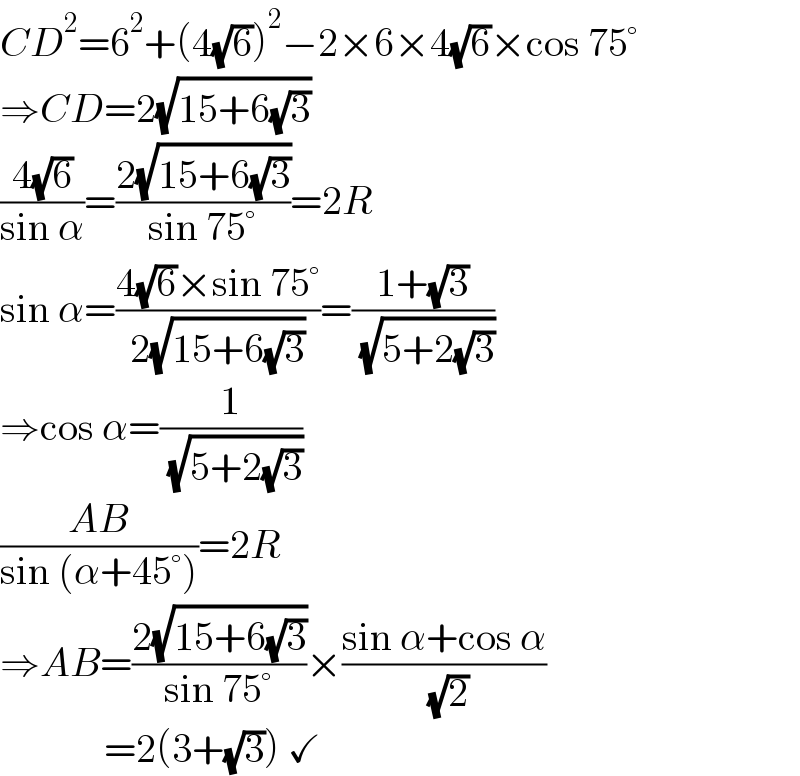
CD^2 =6^2 +(4(√6))^2 −2×6×4(√6)×cos 75° ⇒CD=2(√(15+6(√3))) ((4(√6))/(sin α))=((2(√(15+6(√3))))/(sin 75°))=2R sin α=((4(√6)×sin 75°)/(2(√(15+6(√3)))))=((1+(√3))/( (√(5+2(√3))))) ⇒cos α=(1/( (√(5+2(√3))))) ((AB)/(sin (α+45°)))=2R ⇒AB=((2(√(15+6(√3))))/(sin 75°))×((sin α+cos α)/( (√2))) =2(3+(√3)) ✓

$${CD}^{\mathrm{2}} =\mathrm{6}^{\mathrm{2}} +\left(\mathrm{4}\sqrt{\mathrm{6}}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{6}×\mathrm{4}\sqrt{\mathrm{6}}×\mathrm{cos}\:\mathrm{75}° \\ $$$$\Rightarrow{CD}=\mathrm{2}\sqrt{\mathrm{15}+\mathrm{6}\sqrt{\mathrm{3}}} \\ $$$$\frac{\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{sin}\:\alpha}=\frac{\mathrm{2}\sqrt{\mathrm{15}+\mathrm{6}\sqrt{\mathrm{3}}}}{\mathrm{sin}\:\mathrm{75}°}=\mathrm{2}{R} \\ $$$$\mathrm{sin}\:\alpha=\frac{\mathrm{4}\sqrt{\mathrm{6}}×\mathrm{sin}\:\mathrm{75}°}{\mathrm{2}\sqrt{\mathrm{15}+\mathrm{6}\sqrt{\mathrm{3}}}}=\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{3}}}} \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{3}}}} \\ $$$$\frac{{AB}}{\mathrm{sin}\:\left(\alpha+\mathrm{45}°\right)}=\mathrm{2}{R} \\ $$$$\Rightarrow{AB}=\frac{\mathrm{2}\sqrt{\mathrm{15}+\mathrm{6}\sqrt{\mathrm{3}}}}{\mathrm{sin}\:\mathrm{75}°}×\frac{\mathrm{sin}\:\alpha+\mathrm{cos}\:\alpha}{\:\sqrt{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left(\mathrm{3}+\sqrt{\mathrm{3}}\right)\:\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com