
Question Number 205559 by mnjuly1970 last updated on 24/Mar/24

$$ \\ $$$$\:\:\:{Question}.\:\left({math}\:{analysis}\right) \\ $$$$\:\:\left({X}\:,{d}\:\right)\:{is}\:{a}\:{metric}\:{space}\:{and} \\ $$$$\:\:\left({p}_{{n}} \right)_{{n}=\mathrm{1}} ^{\infty} \:{is}\:{a}\:{sequence}\:{in}\:{X}. \\ $$$$\:\:\:\left({p}_{{n}} \right)_{{n}=\mathrm{1}} ^{\:\infty} {is}\:{cauchy}\:{if}\:{and}\:\:{only}\:{if} \\ $$$$\:\:\:\mathrm{lim}_{\mathrm{N}\rightarrow\infty} {diam}\:\left({E}_{\mathrm{N}} \right)=\mathrm{0}. \\ $$$$\:\:{where}\:,\:{E}_{{N}} \:=\:\left\{\:{p}_{{N}} \:,\:{p}_{{N}+\mathrm{1}} \:,\:...\right\} \\ $$$$\:\:{diam}\:{E}:={sup}\left\{{d}\left({x},{y}\right)\mid{x},{y}\:\in{E}\:\right\} \\ $$$$\:\:\:\: \\ $$
Answered by Berbere last updated on 24/Mar/24
![dim(E)=sup d(x_i ,x_j );(x_i ,x_j )∈E^2 Let p_(n ) a cauchy sequence⇒∀ε>0 ∃N∈N ∣∀k,m≥0 d(P_(N+k) ,P_(N+m) )≤ε......1 E_N {P_N ,P_(N+1) ,.......};let S_N =sup (d(x,y)∣(x,y)∈E_N ^2 ) S_N ∈R since P_N is cauchy Sequence ∃a>0 ⇒d(P_k ,P_l )<a ∀(k,l)∈N^2 if N_1 >N_2 ⇒E_N_2 ⊂E_N_1 ⇒S_N_2 <S_N_1 S_(N ) decrease biunded Sequence ⇒Diam(E_N ) Cv 1...⇒∀ε≥0 ∃N ∈N ∣ diam(E_N )<ε lim_(N→∞) diam(E_N )=a∈R_+ a<diam(E_N ) (E_N decrease)⇒∀ε>0 0≤ a<ε ∀n>0 0≤a≤(1/n)⇒a∈∩^(n∈N^∗ ) [0,(1/n)]={0} ⇒lim_(n→∞) diam(E_N )=0](Q205563.png)
$${dim}\left({E}\right)={sup}\:{d}\left({x}_{{i}} ,{x}_{{j}} \right);\left({x}_{{i}} ,{x}_{{j}} \right)\in{E}^{\mathrm{2}} \\ $$$${Let}\:{p}_{{n}\:} \:{a}\:{cauchy}\:{sequence}\Rightarrow\forall\epsilon>\mathrm{0}\:\exists{N}\in\mathbb{N}\:\mid\forall{k},{m}\geqslant\mathrm{0}\:\:{d}\left({P}_{{N}+{k}} ,{P}_{{N}+{m}} \right)\leqslant\epsilon......\mathrm{1} \\ $$$${E}_{{N}} \left\{{P}_{{N}} ,{P}_{{N}+\mathrm{1}} ,.......\right\};{let}\:{S}_{{N}} ={sup}\:\left({d}\left({x},{y}\right)\mid\left({x},{y}\right)\in{E}_{{N}} ^{\mathrm{2}} \right) \\ $$$${S}_{{N}} \in\mathbb{R}\:{since}\:\:{P}_{{N}} \:{is}\:{cauchy}\:{Sequence}\:\exists{a}>\mathrm{0}\:\Rightarrow{d}\left({P}_{{k}} ,{P}_{{l}} \right)<{a} \\ $$$$\forall\left({k},{l}\right)\in\mathbb{N}^{\mathrm{2}} \\ $$$${if}\:{N}_{\mathrm{1}} >{N}_{\mathrm{2}} \Rightarrow{E}_{{N}_{\mathrm{2}} } \subset{E}_{{N}_{\mathrm{1}} } \Rightarrow{S}_{{N}_{\mathrm{2}} } <{S}_{{N}_{\mathrm{1}} } \:\:{S}_{{N}\:} \:{decrease}\:{biunded}\:{Sequence} \\ $$$$\Rightarrow{Diam}\left({E}_{{N}} \right)\:{Cv} \\ $$$$\mathrm{1}...\Rightarrow\forall\epsilon\geqslant\mathrm{0}\:\:\:\:\exists{N}\:\in\mathbb{N}\:\mid\:{diam}\left({E}_{{N}} \right)<\epsilon \\ $$$$\underset{{N}\rightarrow\infty} {\mathrm{lim}}\:{diam}\left({E}_{{N}} \right)={a}\in\mathbb{R}_{+} \\ $$$${a}<{diam}\left({E}_{{N}} \right)\:\:\left({E}_{{N}} \:{decrease}\right)\Rightarrow\forall\epsilon>\mathrm{0}\:\mathrm{0}\leqslant\:{a}<\epsilon \\ $$$$\forall{n}>\mathrm{0}\:\:\mathrm{0}\leqslant{a}\leqslant\frac{\mathrm{1}}{{n}}\Rightarrow{a}\in\overset{{n}\in\mathbb{N}^{\ast} } {\cap}\left[\mathrm{0},\frac{\mathrm{1}}{{n}}\right]=\left\{\mathrm{0}\right\} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{diam}\left({E}_{{N}} \right)=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 24/Mar/24
$${thanks}\:{alot}\:{sir}\:... \\ $$
Commented by Berbere last updated on 24/Mar/24

$${Withe}\:{Pleasur} \\ $$
Answered by aleks041103 last updated on 04/Apr/24
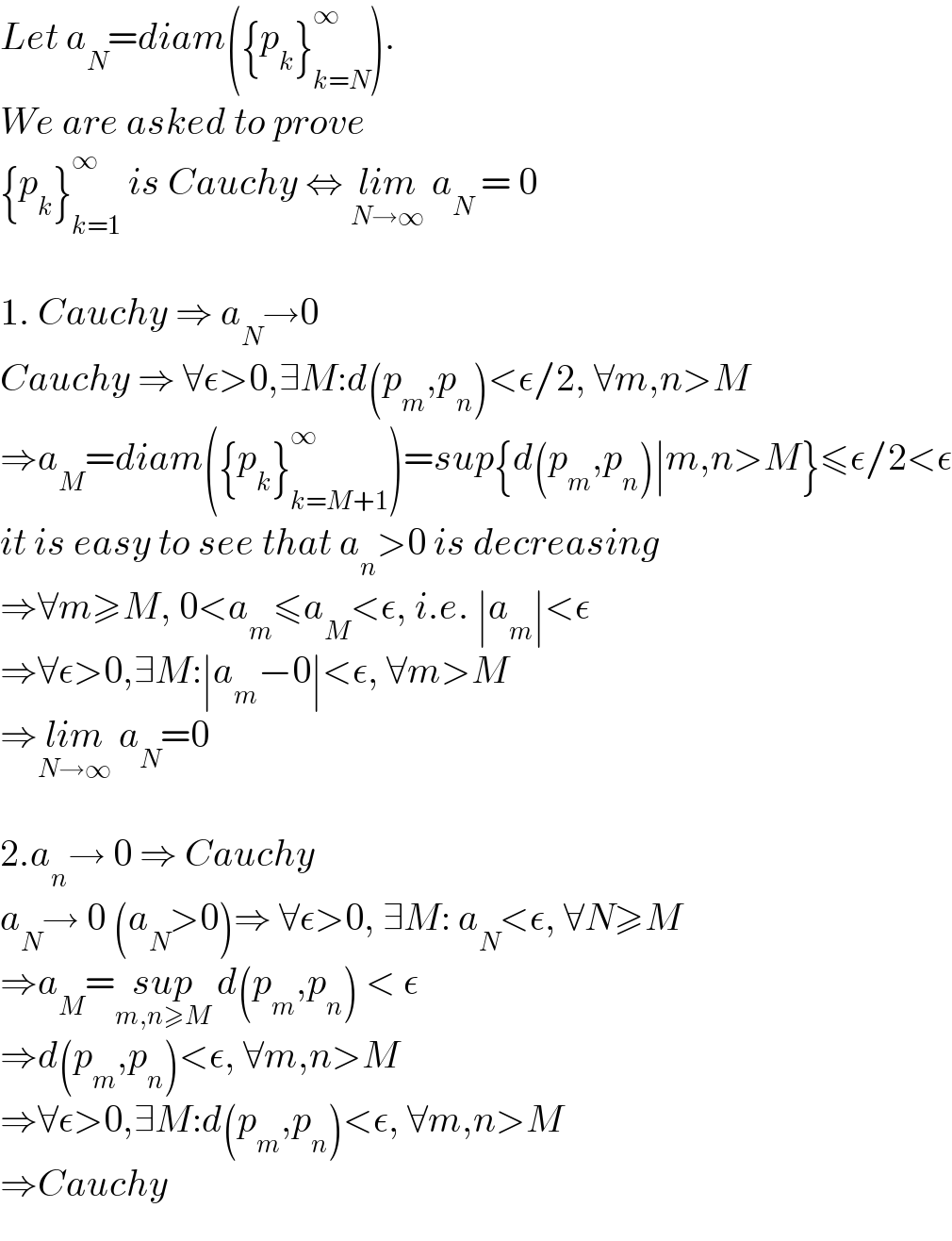
$${Let}\:{a}_{{N}} ={diam}\left(\left\{{p}_{{k}} \right\}_{{k}={N}} ^{\infty} \right). \\ $$$${We}\:{are}\:{asked}\:{to}\:{prove} \\ $$$$\left\{{p}_{{k}} \right\}_{{k}=\mathrm{1}} ^{\infty} \:{is}\:{Cauchy}\:\Leftrightarrow\:\underset{{N}\rightarrow\infty} {{lim}}\:{a}_{{N}} \:=\:\mathrm{0} \\ $$$$ \\ $$$$\mathrm{1}.\:{Cauchy}\:\Rightarrow\:{a}_{{N}} \rightarrow\mathrm{0} \\ $$$${Cauchy}\:\Rightarrow\:\forall\epsilon>\mathrm{0},\exists{M}:{d}\left({p}_{{m}} ,{p}_{{n}} \right)<\epsilon/\mathrm{2},\:\forall{m},{n}>{M} \\ $$$$\Rightarrow{a}_{{M}} ={diam}\left(\left\{{p}_{{k}} \right\}_{{k}={M}+\mathrm{1}} ^{\infty} \right)={sup}\left\{{d}\left({p}_{{m}} ,{p}_{{n}} \right)\mid{m},{n}>{M}\right\}\leqslant\epsilon/\mathrm{2}<\epsilon \\ $$$${it}\:{is}\:{easy}\:{to}\:{see}\:{that}\:{a}_{{n}} >\mathrm{0}\:{is}\:{decreasing} \\ $$$$\Rightarrow\forall{m}\geqslant{M},\:\mathrm{0}<{a}_{{m}} \leqslant{a}_{{M}} <\epsilon,\:{i}.{e}.\:\mid{a}_{{m}} \mid<\epsilon \\ $$$$\Rightarrow\forall\epsilon>\mathrm{0},\exists{M}:\mid{a}_{{m}} −\mathrm{0}\mid<\epsilon,\:\forall{m}>{M} \\ $$$$\Rightarrow\underset{{N}\rightarrow\infty} {{lim}}\:{a}_{{N}} =\mathrm{0} \\ $$$$ \\ $$$$\mathrm{2}.{a}_{{n}} \rightarrow\:\mathrm{0}\:\Rightarrow\:{Cauchy} \\ $$$${a}_{{N}} \rightarrow\:\mathrm{0}\:\left({a}_{{N}} >\mathrm{0}\right)\Rightarrow\:\forall\epsilon>\mathrm{0},\:\exists{M}:\:{a}_{{N}} <\epsilon,\:\forall{N}\geqslant{M} \\ $$$$\Rightarrow{a}_{{M}} =\underset{{m},{n}\geqslant{M}} {{sup}}\:{d}\left({p}_{{m}} ,{p}_{{n}} \right)\:<\:\epsilon \\ $$$$\Rightarrow{d}\left({p}_{{m}} ,{p}_{{n}} \right)<\epsilon,\:\forall{m},{n}>{M} \\ $$$$\Rightarrow\forall\epsilon>\mathrm{0},\exists{M}:{d}\left({p}_{{m}} ,{p}_{{n}} \right)<\epsilon,\:\forall{m},{n}>{M} \\ $$$$\Rightarrow{Cauchy} \\ $$
