
Previous in Differential Equation Next in Differential Equation
Question Number 2051 by Yozzi last updated on 01/Nov/15
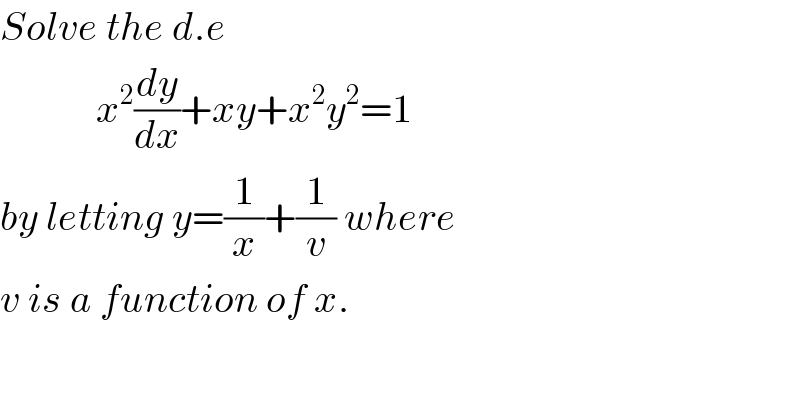
$${Solve}\:{the}\:{d}.{e}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} \frac{{dy}}{{dx}}+{xy}+{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{1} \\ $$$${by}\:{letting}\:{y}=\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{v}}\:{where} \\ $$$${v}\:{is}\:{a}\:{function}\:{of}\:{x}.\: \\ $$
Answered by 123456 last updated on 01/Nov/15
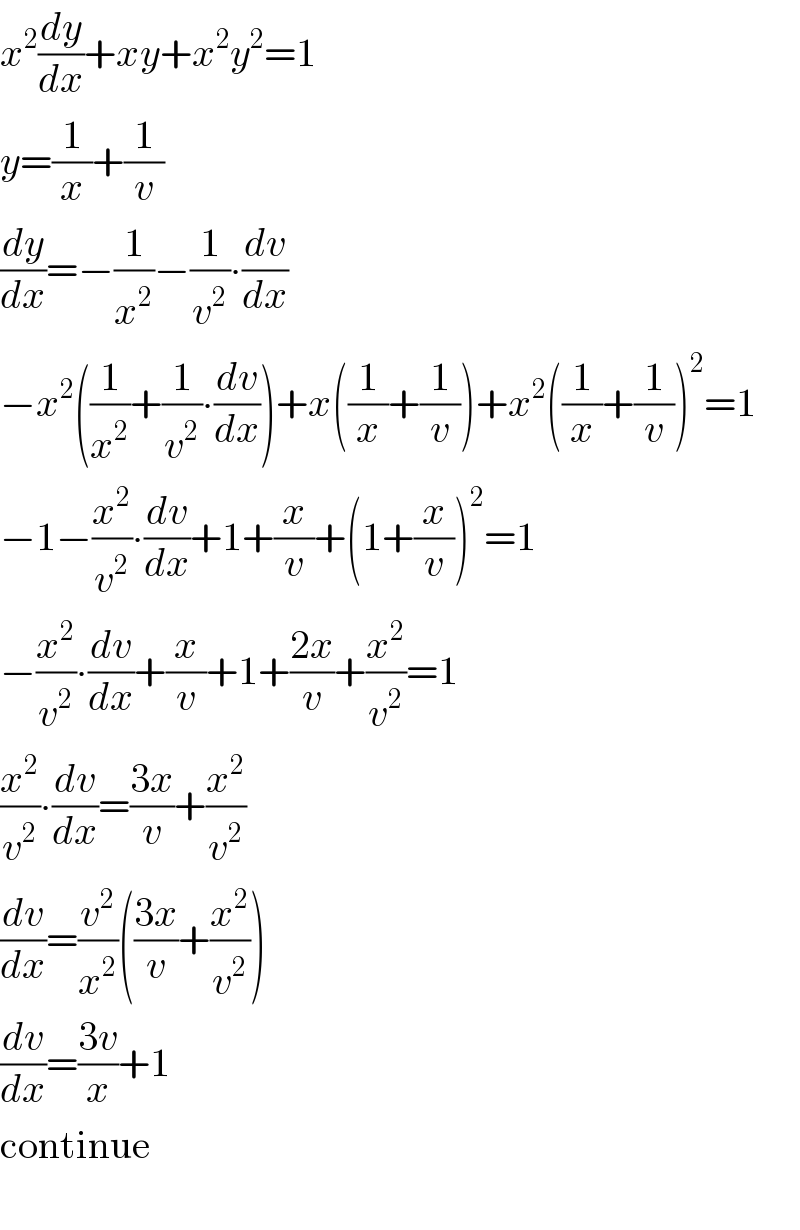
$${x}^{\mathrm{2}} \frac{{dy}}{{dx}}+{xy}+{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{1} \\ $$$${y}=\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{v}} \\ $$$$\frac{{dy}}{{dx}}=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{v}^{\mathrm{2}} }\centerdot\frac{{dv}}{{dx}} \\ $$$$−{x}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{v}^{\mathrm{2}} }\centerdot\frac{{dv}}{{dx}}\right)+{x}\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{v}}\right)+{x}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{v}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$−\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{v}^{\mathrm{2}} }\centerdot\frac{{dv}}{{dx}}+\mathrm{1}+\frac{{x}}{{v}}+\left(\mathrm{1}+\frac{{x}}{{v}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$−\frac{{x}^{\mathrm{2}} }{{v}^{\mathrm{2}} }\centerdot\frac{{dv}}{{dx}}+\frac{{x}}{{v}}+\mathrm{1}+\frac{\mathrm{2}{x}}{{v}}+\frac{{x}^{\mathrm{2}} }{{v}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{x}^{\mathrm{2}} }{{v}^{\mathrm{2}} }\centerdot\frac{{dv}}{{dx}}=\frac{\mathrm{3}{x}}{{v}}+\frac{{x}^{\mathrm{2}} }{{v}^{\mathrm{2}} } \\ $$$$\frac{{dv}}{{dx}}=\frac{{v}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\left(\frac{\mathrm{3}{x}}{{v}}+\frac{{x}^{\mathrm{2}} }{{v}^{\mathrm{2}} }\right) \\ $$$$\frac{{dv}}{{dx}}=\frac{\mathrm{3}{v}}{{x}}+\mathrm{1} \\ $$$$\mathrm{continue} \\ $$$$ \\ $$
Commented by prakash jain last updated on 01/Nov/15

$${v}=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} {x}^{{i}} \\ $$$${v}'=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{ia}_{{i}} {x}^{{i}−\mathrm{1}} \\ $$$$\frac{\mathrm{3}{v}}{{x}}=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{3}{a}_{{i}} {x}^{{i}−\mathrm{1}} \\ $$$${v}'=\frac{\mathrm{3}{v}}{{x}}+\mathrm{1} \\ $$$${equating}\:{coeffiients} \\ $$$${a}_{\mathrm{1}} =\mathrm{3}{a}_{\mathrm{1}} +\mathrm{1}\Rightarrow{a}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}{a}_{\mathrm{2}} =\mathrm{3}{a}_{\mathrm{2}} \Rightarrow{a}_{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{3}{a}_{\mathrm{3}} =\mathrm{3}{a}_{\mathrm{3}} \Rightarrow{a}_{\mathrm{3}} ={c} \\ $$$$\mathrm{4}{a}_{\mathrm{4}} =\mathrm{3}{a}_{\mathrm{4}} \Rightarrow{a}_{\mathrm{4}} =\mathrm{0}\:{also}\:{a}_{\mathrm{5}} ,...{a}_{{n}} =\mathrm{0} \\ $$$${v}={cx}^{\mathrm{3}} −\frac{{x}}{\mathrm{2}} \\ $$
