
Previous in Differential Equation Next in Differential Equation
Question Number 2050 by Yozzi last updated on 01/Nov/15
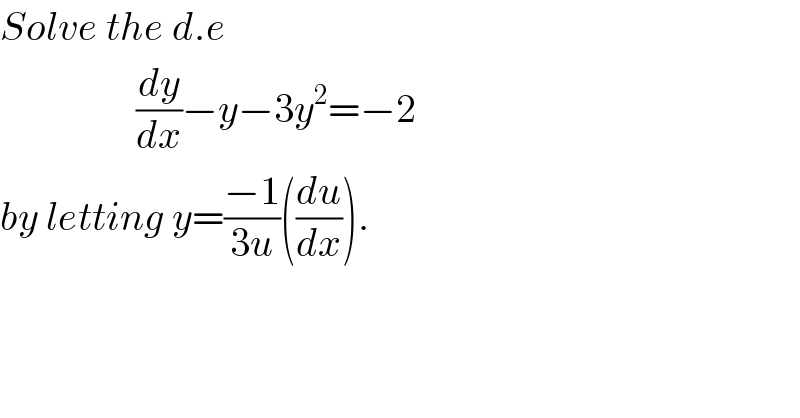
$${Solve}\:{the}\:{d}.{e} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{dy}}{{dx}}−{y}−\mathrm{3}{y}^{\mathrm{2}} =−\mathrm{2}\: \\ $$$${by}\:{letting}\:{y}=\frac{−\mathrm{1}}{\mathrm{3}{u}}\left(\frac{{du}}{{dx}}\right). \\ $$
Answered by 123456 last updated on 01/Nov/15
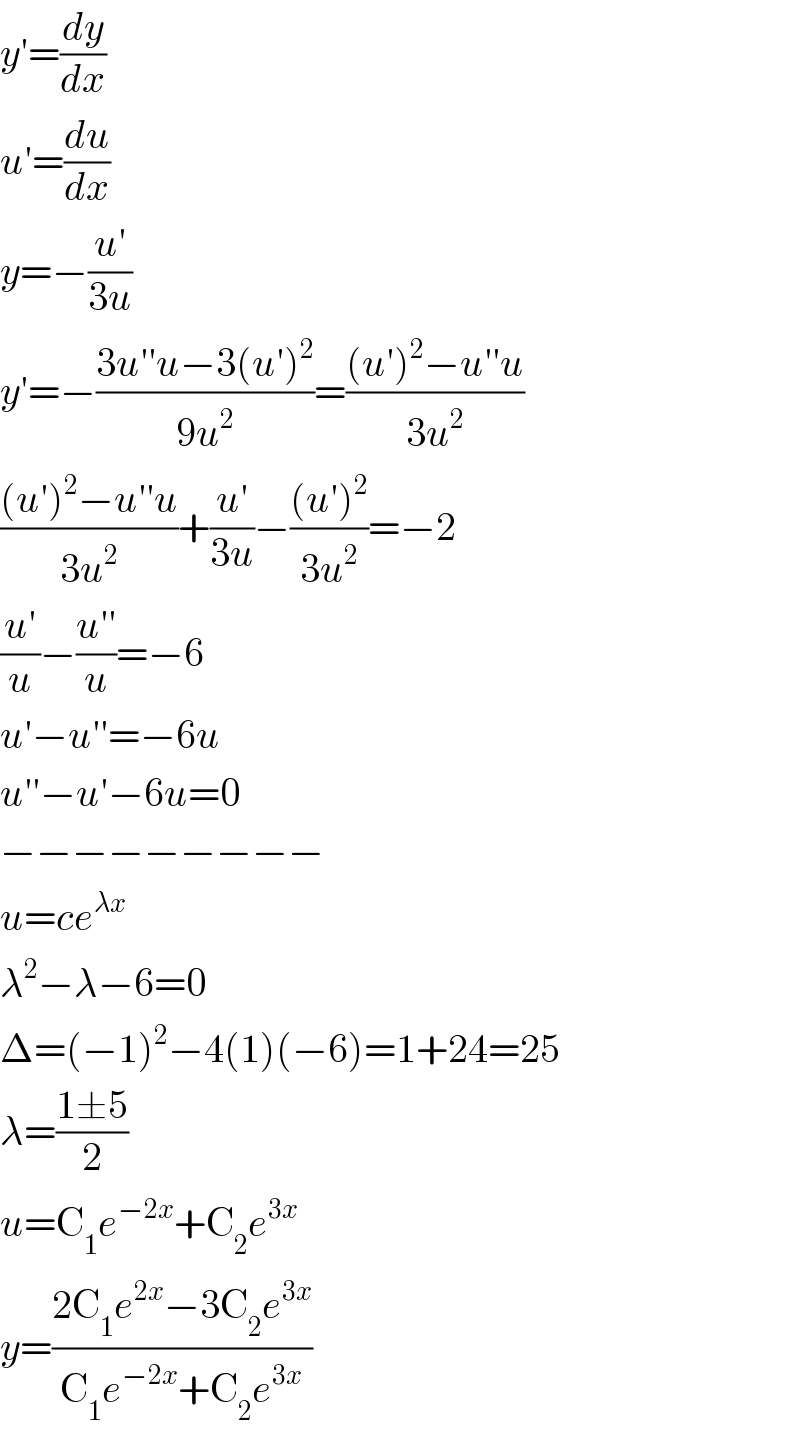
$${y}'=\frac{{dy}}{{dx}} \\ $$$${u}'=\frac{{du}}{{dx}} \\ $$$${y}=−\frac{{u}'}{\mathrm{3}{u}} \\ $$$${y}'=−\frac{\mathrm{3}{u}''{u}−\mathrm{3}\left({u}'\right)^{\mathrm{2}} }{\mathrm{9}{u}^{\mathrm{2}} }=\frac{\left({u}'\right)^{\mathrm{2}} −{u}''{u}}{\mathrm{3}{u}^{\mathrm{2}} } \\ $$$$\frac{\left({u}'\right)^{\mathrm{2}} −{u}''{u}}{\mathrm{3}{u}^{\mathrm{2}} }+\frac{{u}'}{\mathrm{3}{u}}−\frac{\left({u}'\right)^{\mathrm{2}} }{\mathrm{3}{u}^{\mathrm{2}} }=−\mathrm{2} \\ $$$$\frac{{u}'}{{u}}−\frac{{u}''}{{u}}=−\mathrm{6} \\ $$$${u}'−{u}''=−\mathrm{6}{u} \\ $$$${u}''−{u}'−\mathrm{6}{u}=\mathrm{0} \\ $$$$−−−−−−−−− \\ $$$${u}={ce}^{\lambda{x}} \\ $$$$\lambda^{\mathrm{2}} −\lambda−\mathrm{6}=\mathrm{0} \\ $$$$\Delta=\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(−\mathrm{6}\right)=\mathrm{1}+\mathrm{24}=\mathrm{25} \\ $$$$\lambda=\frac{\mathrm{1}\pm\mathrm{5}}{\mathrm{2}} \\ $$$${u}=\mathrm{C}_{\mathrm{1}} {e}^{−\mathrm{2}{x}} +\mathrm{C}_{\mathrm{2}} {e}^{\mathrm{3}{x}} \\ $$$${y}=\frac{\mathrm{2C}_{\mathrm{1}} {e}^{\mathrm{2}{x}} −\mathrm{3C}_{\mathrm{2}} {e}^{\mathrm{3}{x}} }{\mathrm{C}_{\mathrm{1}} {e}^{−\mathrm{2}{x}} +\mathrm{C}_{\mathrm{2}} {e}^{\mathrm{3}{x}} } \\ $$
