Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 204545 by hardmath last updated on 21/Feb/24

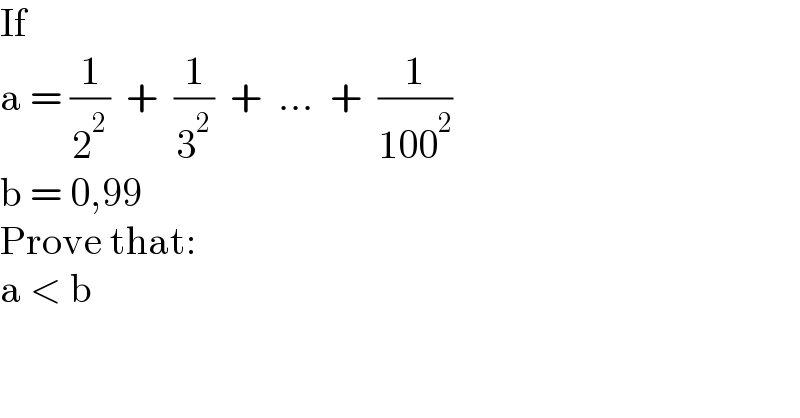
If a = (1/2^2 ) + (1/3^2 ) + ... + (1/(100^2 )) b = 0,99 Prove that: a < b

$$\mathrm{If} \\ $$$$\mathrm{a}\:=\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:\:+\:\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\:\:+\:\:...\:\:+\:\:\frac{\mathrm{1}}{\mathrm{100}^{\mathrm{2}} } \\ $$$$\mathrm{b}\:=\:\mathrm{0},\mathrm{99} \\ $$$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\mathrm{a}\:<\:\mathrm{b} \\ $$

Answered by mr W last updated on 21/Feb/24

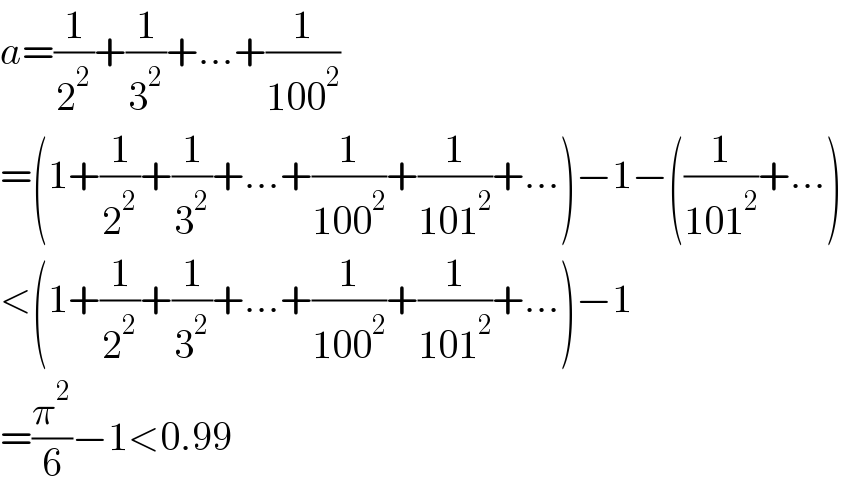
a=(1/2^2 )+(1/3^2 )+...+(1/(100^2 )) =(1+(1/2^2 )+(1/3^2 )+...+(1/(100^2 ))+(1/(101^2 ))+...)−1−((1/(101^2 ))+...) <(1+(1/2^2 )+(1/3^2 )+...+(1/(100^2 ))+(1/(101^2 ))+...)−1 =(π^2 /6)−1<0.99

$${a}=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+...+\frac{\mathrm{1}}{\mathrm{100}^{\mathrm{2}} } \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+...+\frac{\mathrm{1}}{\mathrm{100}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{101}^{\mathrm{2}} }+...\right)−\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{101}^{\mathrm{2}} }+...\right) \\ $$$$<\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+...+\frac{\mathrm{1}}{\mathrm{100}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{101}^{\mathrm{2}} }+...\right)−\mathrm{1} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1}<\mathrm{0}.\mathrm{99} \\ $$

Answered by witcher3 last updated on 21/Feb/24

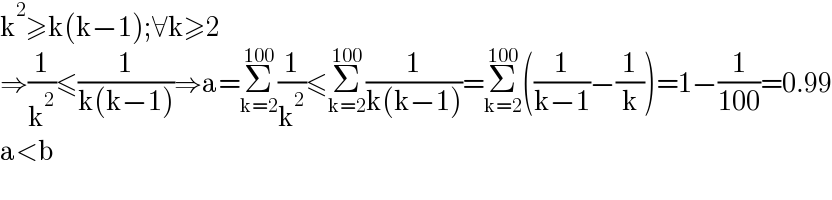
k^2 ≥k(k−1);∀k≥2 ⇒(1/k^2 )≤(1/(k(k−1)))⇒a=Σ_(k=2) ^(100) (1/k^2 )≤Σ_(k=2) ^(100) (1/(k(k−1)))=Σ_(k=2) ^(100) ((1/(k−1))−(1/k))=1−(1/(100))=0.99 a<b

$$\mathrm{k}^{\mathrm{2}} \geqslant\mathrm{k}\left(\mathrm{k}−\mathrm{1}\right);\forall\mathrm{k}\geqslant\mathrm{2} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }\leqslant\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{k}−\mathrm{1}\right)}\Rightarrow\mathrm{a}=\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{100}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }\leqslant\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{100}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{k}−\mathrm{1}\right)}=\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{100}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{k}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{100}}=\mathrm{0}.\mathrm{99} \\ $$$$\mathrm{a}<\mathrm{b} \\ $$

Commented by mr W last updated on 21/Feb/24

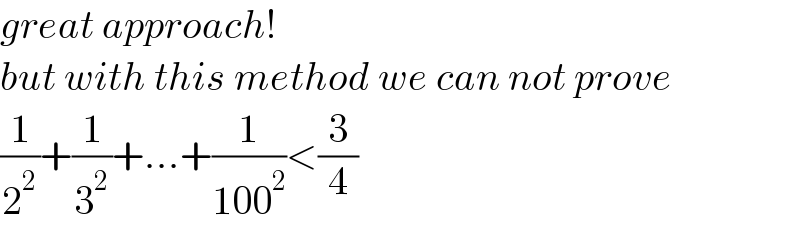
great approach! but with this method we can not prove (1/2^2 )+(1/3^2 )+...+(1/(100^2 ))<(3/4)

$${great}\:{approach}! \\ $$$${but}\:{with}\:{this}\:{method}\:{we}\:{can}\:{not}\:{prove} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+...+\frac{\mathrm{1}}{\mathrm{100}^{\mathrm{2}} }<\frac{\mathrm{3}}{\mathrm{4}} \\ $$

Commented by witcher3 last updated on 22/Feb/24

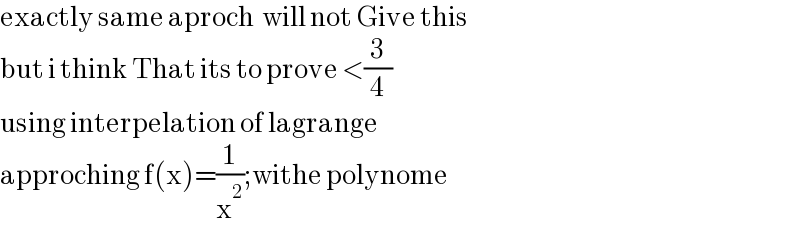
exactly same aproch will not Give this but i think That its to prove <(3/4) using interpelation of lagrange approching f(x)=(1/x^2 );withe polynome

$$\mathrm{exactly}\:\mathrm{same}\:\mathrm{aproch}\:\:\mathrm{will}\:\mathrm{not}\:\mathrm{Give}\:\mathrm{this} \\ $$$$\mathrm{but}\:\mathrm{i}\:\mathrm{think}\:\mathrm{That}\:\mathrm{its}\:\mathrm{to}\:\mathrm{prove}\:<\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{using}\:\mathrm{interpelation}\:\mathrm{of}\:\mathrm{lagrange} \\ $$$$\mathrm{approching}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} };\mathrm{withe}\:\mathrm{polynome} \\ $$

Commented by mr W last updated on 22/Feb/24

thanks alot!

$${thanks}\:{alot}! \\ $$

Commented by hardmath last updated on 23/Feb/24

thank you dear professors

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professors} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com