
Question Number 204518 by Abdullahrussell last updated on 20/Feb/24
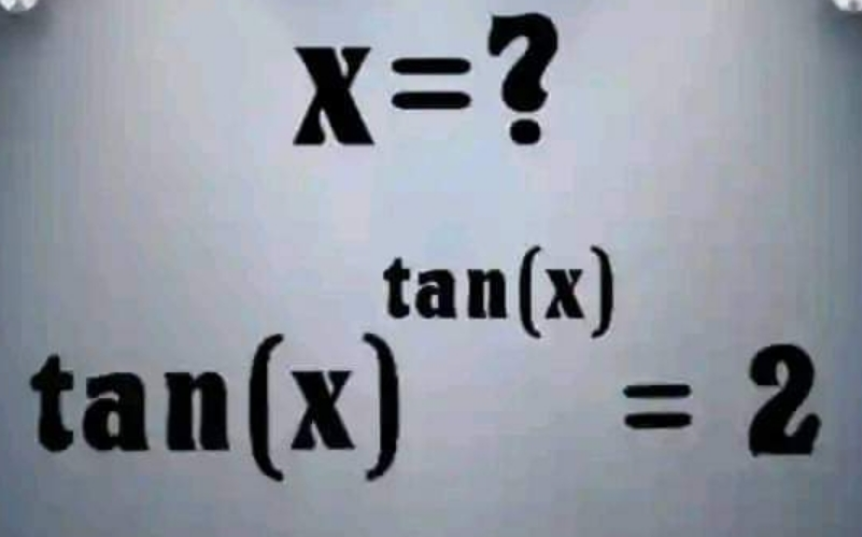
Answered by TonyCWX08 last updated on 20/Feb/24

$$ \\ $$$${let}\:{us}\:{solve}\:{y}^{{y}} =\mathrm{2}\:{first} \\ $$$${y}^{{y}} =\mathrm{2} \\ $$$${y}=\mathrm{2}^{\frac{\mathrm{1}}{{y}}} \\ $$$${y}=\left({e}^{{ln}\left(\mathrm{2}\right)} \right)^{\frac{\mathrm{1}}{{y}}} \\ $$$${y}={e}^{\frac{{ln}\left(\mathrm{2}\right)}{{y}}} \\ $$$${ln}\left(\mathrm{2}\right)=\frac{{ln}\left(\mathrm{2}\right)}{{y}}{e}^{\frac{{ln}\left(\mathrm{2}\right)}{{y}}} \\ $$$${Using}\:{LambertW}\:{function}, \\ $$$${W}\left({ln}\left(\mathrm{2}\right)\right)\:=\:\frac{{ln}\left(\mathrm{2}\right)}{{y}} \\ $$$${y}=\frac{{ln}\left(\mathrm{2}\right)}{{W}\left({ln}\left(\mathrm{2}\right)\right)} \\ $$$${y}\:=\:{e}^{{W}\left({ln}\left(\mathrm{2}\right)\right)} \\ $$$${According}\:{to}\:{WolframAlpha}, \\ $$$${e}^{{W}\left({ln}\left(\mathrm{2}\right)\right)} \approx\mathrm{1}.\mathrm{55961}={y} \\ $$$$ \\ $$$${So} \\ $$$${y}^{{y}} =\mathrm{2} \\ $$$$\mathrm{1}.\mathrm{55961}^{\mathrm{1}.\mathrm{55961}} =\mathrm{2} \\ $$$${tan}\left({x}\right)^{{tan}\left({x}\right)} =\mathrm{1}.\mathrm{55961}^{\mathrm{1}.\mathrm{55961}} \\ $$$${tan}\left({x}\right)=\mathrm{1}.\mathrm{55961} \\ $$$${x}=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}.\mathrm{55961}\right) \\ $$$${x}=\mathrm{1}.\mathrm{00064}+{k}\pi\:,\:{k}\in{Z} \\ $$
