
Question Number 2045 by prakash jain last updated on 31/Oct/15
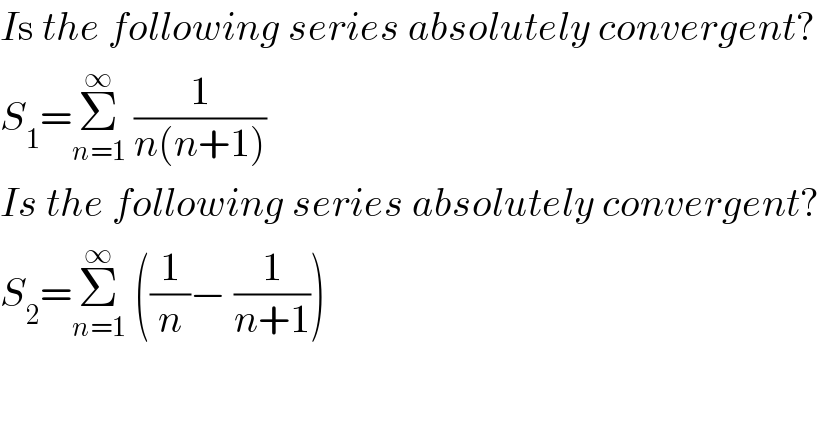
$${I}\mathrm{s}\:{the}\:{following}\:{series}\:{absolutely}\:{convergent}? \\ $$$${S}_{\mathrm{1}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)} \\ $$$${Is}\:{the}\:{following}\:{series}\:{absolutely}\:{convergent}? \\ $$$${S}_{\mathrm{2}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left(\frac{\mathrm{1}}{{n}}−\:\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$
Commented by 123456 last updated on 31/Oct/15
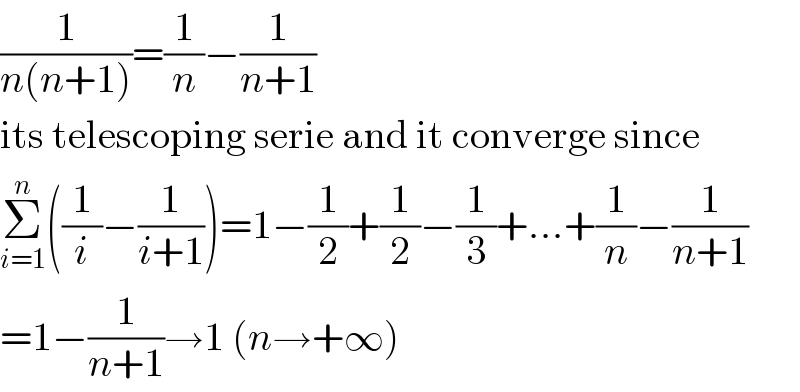
$$\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}=\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\mathrm{its}\:\mathrm{telescoping}\:\mathrm{serie}\:\mathrm{and}\:\mathrm{it}\:\mathrm{converge}\:\mathrm{since} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{{i}}−\frac{\mathrm{1}}{{i}+\mathrm{1}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+...+\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\rightarrow\mathrm{1}\:\left({n}\rightarrow+\infty\right) \\ $$
Commented by prakash jain last updated on 31/Oct/15

$$\mathrm{So}\:{S}_{\mathrm{1}} ={S}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{convergent}.\:\mathrm{Then}\:\mathrm{it}\:\mathrm{has}\:\mathrm{to}\:\mathrm{be}\:\mathrm{absolutely} \\ $$$$\mathrm{convergent},\:\mathrm{since}\:\mathrm{each}\:\mathrm{term}\:\mathrm{is}\:+\mathrm{ve}. \\ $$
