
Question Number 204039 by hardmath last updated on 04/Feb/24
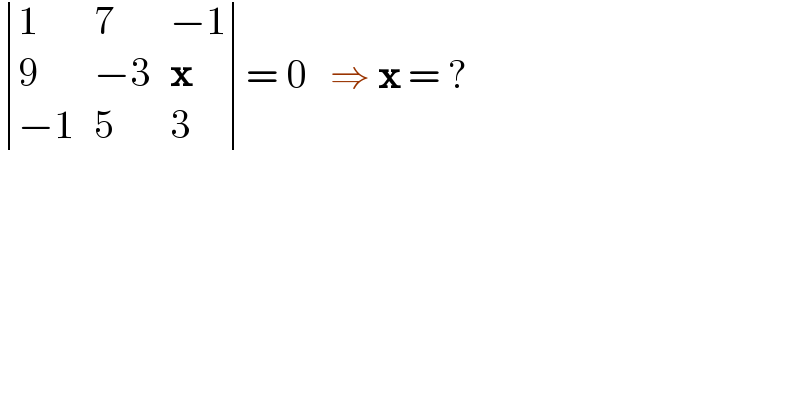
$$\begin{vmatrix}{\mathrm{1}}&{\mathrm{7}}&{−\mathrm{1}}\\{\mathrm{9}}&{−\mathrm{3}}&{\boldsymbol{\mathrm{x}}}\\{−\mathrm{1}}&{\mathrm{5}}&{\mathrm{3}}\end{vmatrix}=\:\mathrm{0}\:\:\:\Rightarrow\:\boldsymbol{\mathrm{x}}\:=\:? \\ $$
Answered by deleteduser1 last updated on 04/Feb/24
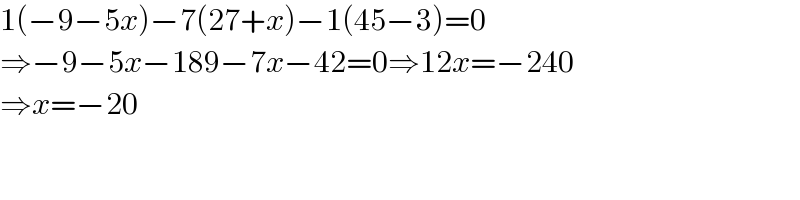
$$\mathrm{1}\left(−\mathrm{9}−\mathrm{5}{x}\right)−\mathrm{7}\left(\mathrm{27}+{x}\right)−\mathrm{1}\left(\mathrm{45}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow−\mathrm{9}−\mathrm{5}{x}−\mathrm{189}−\mathrm{7}{x}−\mathrm{42}=\mathrm{0}\Rightarrow\mathrm{12}{x}=−\mathrm{240} \\ $$$$\Rightarrow{x}=−\mathrm{20} \\ $$
Answered by Rasheed.Sindhi last updated on 05/Feb/24
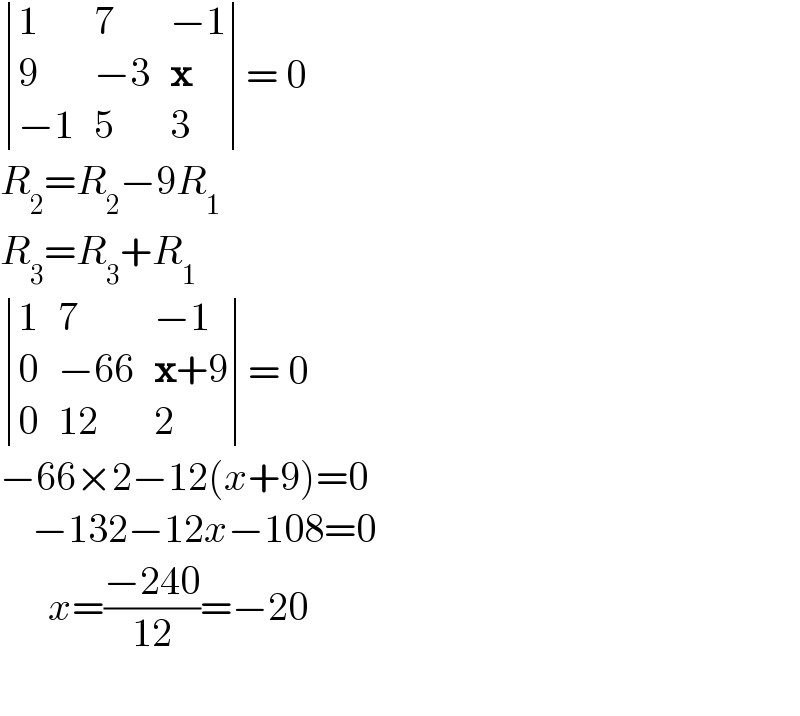
$$\begin{vmatrix}{\mathrm{1}}&{\mathrm{7}}&{−\mathrm{1}}\\{\mathrm{9}}&{−\mathrm{3}}&{\boldsymbol{\mathrm{x}}}\\{−\mathrm{1}}&{\mathrm{5}}&{\mathrm{3}}\end{vmatrix}=\:\mathrm{0} \\ $$$${R}_{\mathrm{2}} ={R}_{\mathrm{2}} −\mathrm{9}{R}_{\mathrm{1}} \\ $$$${R}_{\mathrm{3}} ={R}_{\mathrm{3}} +{R}_{\mathrm{1}} \\ $$$$\begin{vmatrix}{\mathrm{1}}&{\mathrm{7}}&{−\mathrm{1}}\\{\mathrm{0}}&{−\mathrm{66}}&{\boldsymbol{\mathrm{x}}+\mathrm{9}}\\{\mathrm{0}}&{\mathrm{12}}&{\mathrm{2}}\end{vmatrix}=\:\mathrm{0} \\ $$$$−\mathrm{66}×\mathrm{2}−\mathrm{12}\left({x}+\mathrm{9}\right)=\mathrm{0} \\ $$$$\:\:\:\:−\mathrm{132}−\mathrm{12}{x}−\mathrm{108}=\mathrm{0} \\ $$$$\:\:\:\:\:\:{x}=\frac{−\mathrm{240}}{\mathrm{12}}=−\mathrm{20} \\ $$$$ \\ $$
Commented by hardmath last updated on 05/Feb/24
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professors} \\ $$
