
Question Number 204018 by mnjuly1970 last updated on 04/Feb/24
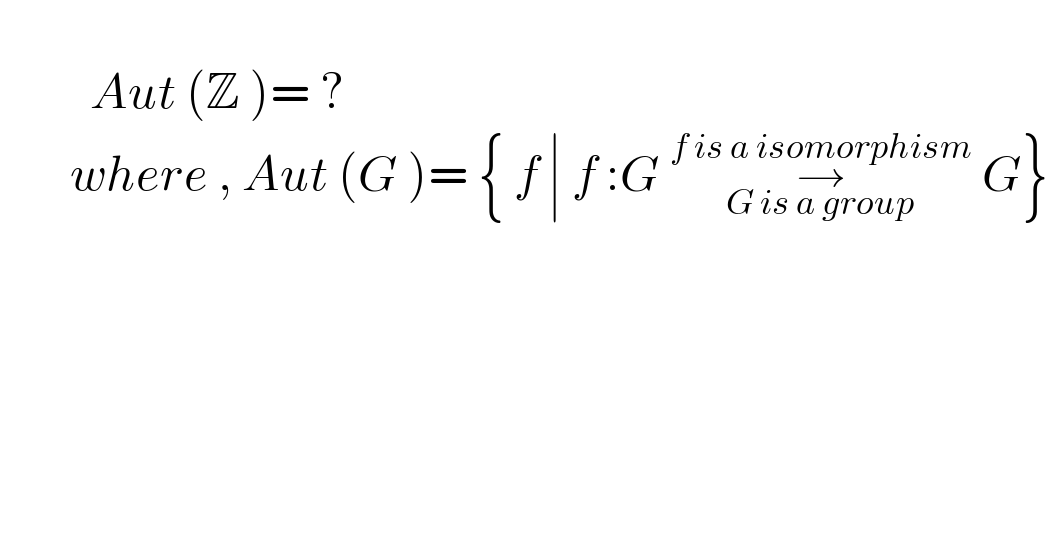
$$ \\ $$$$\:\:\:\:\:\:\:\:\:{Aut}\:\left(\mathbb{Z}\:\right)=\:? \\ $$$$\:\:\:\:\:\:\:{where}\:,\:{Aut}\:\left({G}\:\right)=\:\left\{\:{f}\:\mid\:{f}\::{G}\:\underset{{G}\:{is}\:{a}\:{group}} {\overset{{f}\:{is}\:{a}\:{isomorphism}} {\rightarrow}}\:{G}\right\} \\ $$
Answered by witcher3 last updated on 04/Feb/24

$$\mathrm{f}\in\mathrm{Aut}\left(\mathrm{G}\right) \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{1}\right)=\mathrm{a}\in\mathbb{Z} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{n}\right)=\mathrm{na}\: \\ $$$$\mathrm{suppose}\:\mid\mathrm{a}\mid>\mathrm{1}\Rightarrow\exists\mathrm{p}\in\mathrm{IP}\:\:\mathrm{p}\mid\mathrm{a} \\ $$$$\Rightarrow\mathrm{1}\notin\mathrm{f}\left(\mathbb{Z}\right)?\mathrm{since}\:\:\mathrm{1}=\mathrm{ap}\Rightarrow\mathrm{p}\mid\mathrm{1}\:\mathrm{impossibl} \\ $$$$\Rightarrow\mid\mathrm{a}\mid\leqslant\mathrm{1} \\ $$$$\mathrm{a}=\mathrm{0}\Rightarrow\mathrm{f}=\mathrm{0}\:\mathrm{not}\:\mathrm{bijective} \\ $$$$\Rightarrow\mathrm{a}\in\left\{\mathrm{1},−\mathrm{1}\right\} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\begin{cases}{\mathrm{x}}\\{−\boldsymbol{\mathrm{x}}}\end{cases} \\ $$$$\boldsymbol{\mathrm{f}}=\boldsymbol{\mathrm{id}};−\mathrm{id}\:\mathrm{worcks} \\ $$
Commented by mnjuly1970 last updated on 04/Feb/24

$$ \\ $$
Commented by witcher3 last updated on 04/Feb/24

$$\mathrm{withe}\:\mathrm{Pleasur} \\ $$
