
Question Number 203807 by aba last updated on 28/Jan/24
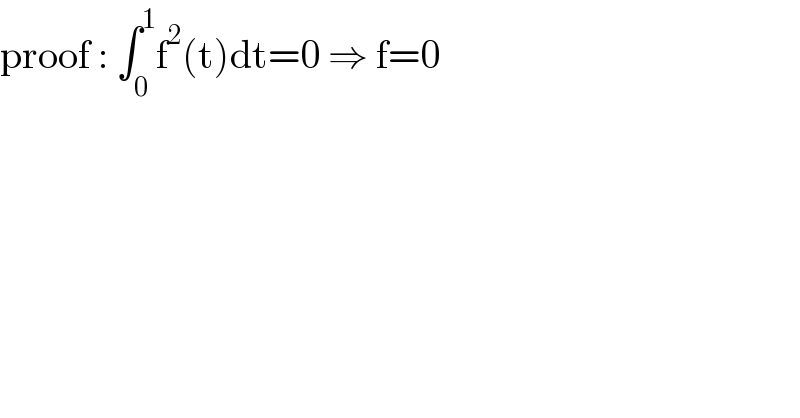
$$\mathrm{proof}\::\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{f}^{\mathrm{2}} \left(\mathrm{t}\right)\mathrm{dt}=\mathrm{0}\:\Rightarrow\:\mathrm{f}=\mathrm{0} \\ $$
Answered by JDamian last updated on 28/Jan/24

$$ \\ $$$$\mathrm{f}^{\mathrm{2}} \left(\mathrm{t}\right)\geqslant\mathrm{0}\:\:\:\:\forall{t} \\ $$$$ \\ $$
Answered by witcher3 last updated on 29/Jan/24
![f is continus we can f(x)= { ((1 is x∈IQ)),((0 if x∉IQ)) :} ∫_0 ^1 f^2 (x)dx=∫_(x∈IQ ∩[0,1]) 1 dx=μ[[0,1]∩Q]=0 or f≠0 if f is continus in[0,1] suppse f≠0 ⇒∃a∈]0,1[ ∣f(a)≠0 ⇒∃ ε>0 such ∀x∈“I=[a−ε,a+ε] f(x)≠0 ⇒∀x∈I f^2 (x)>0 since f is continus is bounded in compact interval ⇒y∈I such f^2 (x)≥f^2 (y)>0 0≥∫_0 ^1 f^2 (x)dx≥∫_I f^2 (x)dx≥∫_I f^2 (y)=f^2 (y).(2ε) ⇒f^2 (y).2ε=0⇒f(y)=0 absurd ⇒f=0](Q203820.png)
$$\mathrm{f}\:\mathrm{is}\:\mathrm{continus}\: \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{f}\left(\mathrm{x}\right)=\begin{cases}{\mathrm{1}\:\mathrm{is}\:\mathrm{x}\in\mathrm{IQ}}\\{\mathrm{0}\:\mathrm{if}\:\mathrm{x}\notin\mathrm{IQ}}\end{cases} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx}=\int_{\mathrm{x}\in\mathrm{IQ}\:\cap\left[\mathrm{0},\mathrm{1}\right]} \mathrm{1}\:\mathrm{dx}=\mu\left[\left[\mathrm{0},\mathrm{1}\right]\cap\mathrm{Q}\right]=\mathrm{0} \\ $$$$\mathrm{or}\:\mathrm{f}\neq\mathrm{0} \\ $$$$\mathrm{if}\:\mathrm{f}\:\mathrm{is}\:\mathrm{continus}\:\mathrm{in}\left[\mathrm{0},\mathrm{1}\right] \\ $$$$\left.\mathrm{suppse}\:\mathrm{f}\neq\mathrm{0}\:\Rightarrow\exists\mathrm{a}\in\right]\mathrm{0},\mathrm{1}\left[\:\mid\mathrm{f}\left(\mathrm{a}\right)\neq\mathrm{0}\right. \\ $$$$\Rightarrow\exists\:\epsilon>\mathrm{0}\:\mathrm{such}\:\forall\mathrm{x}\in``\mathrm{I}=\left[\mathrm{a}−\epsilon,\mathrm{a}+\epsilon\right]\:\mathrm{f}\left(\mathrm{x}\right)\neq\mathrm{0} \\ $$$$\Rightarrow\forall\mathrm{x}\in\mathrm{I}\:\:\:\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)>\mathrm{0}\:\mathrm{since}\:\mathrm{f}\:\mathrm{is}\:\mathrm{continus}\:\mathrm{is}\:\mathrm{bounded}\:\mathrm{in}\:\mathrm{compact} \\ $$$$\mathrm{interval}\:\Rightarrow\mathrm{y}\in\mathrm{I}\:\mathrm{such}\:\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)\geqslant\mathrm{f}^{\mathrm{2}} \left(\mathrm{y}\right)>\mathrm{0} \\ $$$$\mathrm{0}\geqslant\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx}\geqslant\int_{\mathrm{I}} \:\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx}\geqslant\int_{\mathrm{I}} \mathrm{f}^{\mathrm{2}} \left(\mathrm{y}\right)=\mathrm{f}^{\mathrm{2}} \left(\mathrm{y}\right).\left(\mathrm{2}\epsilon\right) \\ $$$$\Rightarrow\mathrm{f}^{\mathrm{2}} \left(\mathrm{y}\right).\mathrm{2}\epsilon=\mathrm{0}\Rightarrow\mathrm{f}\left(\mathrm{y}\right)=\mathrm{0}\:\mathrm{absurd} \\ $$$$\Rightarrow\mathrm{f}=\mathrm{0} \\ $$
