
Question Number 203533 by Mastermind last updated on 21/Jan/24
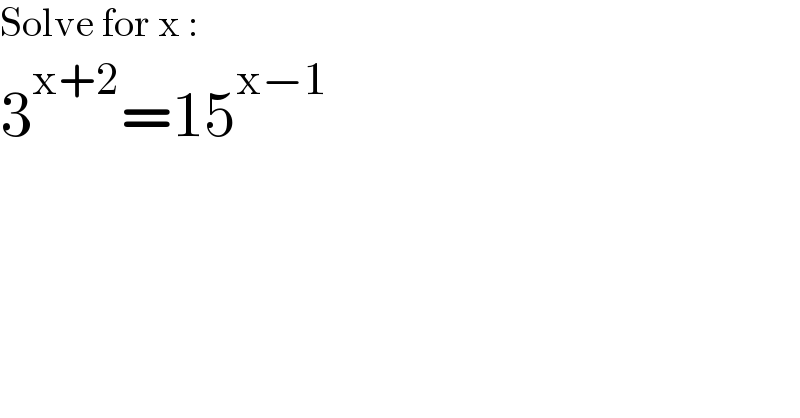
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{x}\:: \\ $$$$\mathrm{3}^{\mathrm{x}+\mathrm{2}} =\mathrm{15}^{\mathrm{x}−\mathrm{1}} \\ $$
Answered by Rasheed.Sindhi last updated on 21/Jan/24
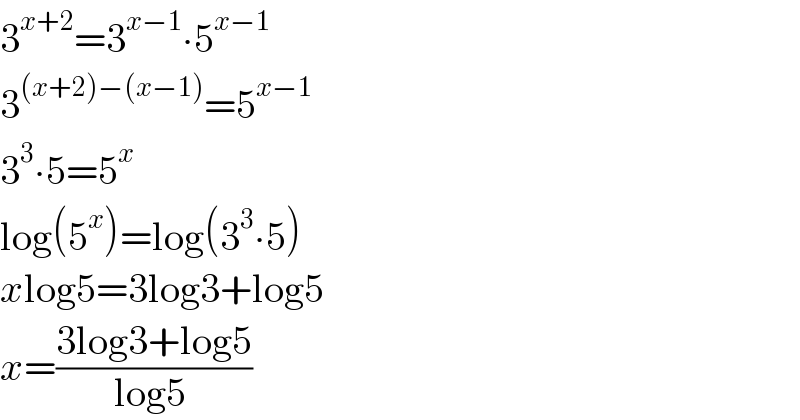
$$\mathrm{3}^{{x}+\mathrm{2}} =\mathrm{3}^{{x}−\mathrm{1}} \centerdot\mathrm{5}^{{x}−\mathrm{1}} \\ $$$$\mathrm{3}^{\left({x}+\mathrm{2}\right)−\left({x}−\mathrm{1}\right)} =\mathrm{5}^{{x}−\mathrm{1}} \\ $$$$\mathrm{3}^{\mathrm{3}} \centerdot\mathrm{5}=\mathrm{5}^{{x}} \\ $$$$\mathrm{log}\left(\mathrm{5}^{{x}} \right)=\mathrm{log}\left(\mathrm{3}^{\mathrm{3}} \centerdot\mathrm{5}\right) \\ $$$${x}\mathrm{log5}=\mathrm{3log3}+\mathrm{log5} \\ $$$${x}=\frac{\mathrm{3log3}+\mathrm{log5}}{\mathrm{log5}\:}\:\:\: \\ $$
Commented by Mastermind last updated on 21/Jan/24
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much},\:\mathrm{man} \\ $$$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate} \\ $$
Answered by Skabetix last updated on 21/Jan/24

$${x}={log}_{\mathrm{5}} \left(\mathrm{135}\right) \\ $$
Commented by Mastermind last updated on 21/Jan/24

$$\mathrm{Thank}\:\mathrm{you} \\ $$
