Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 203171 by a.lgnaoui last updated on 11/Jan/24

Ratio of green blue and Red triangles? Evaluate these Area for 𝛂=25° and length of aquart=1

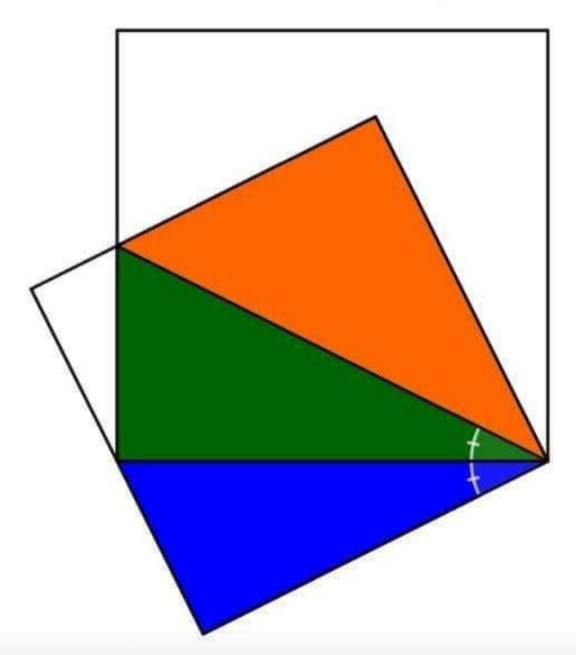
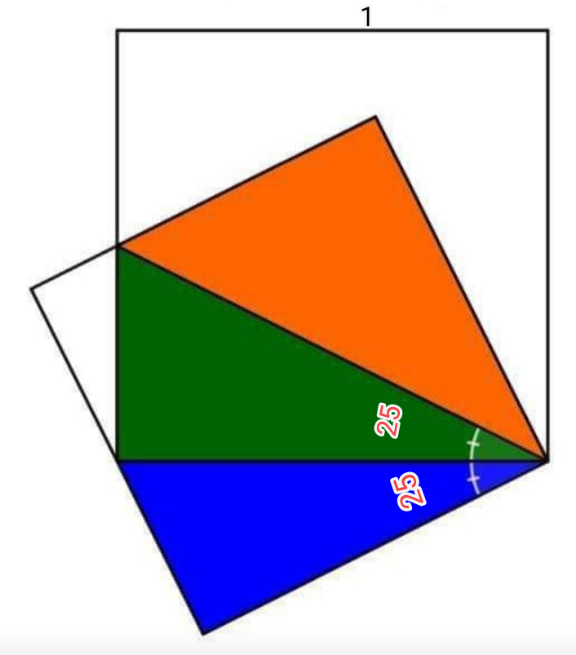
$$\mathrm{Ratio}\:\mathrm{of}\:\mathrm{green}\:\mathrm{blue}\:\mathrm{and}\:\mathrm{Red}\:\mathrm{triangles}? \\ $$$$\mathrm{Evaluate}\:\mathrm{these}\:\mathrm{Area}\:\mathrm{for}\:\boldsymbol{\alpha}=\mathrm{25}°\:\:\mathrm{and} \\ $$$$\mathrm{length}\:\mathrm{of}\:\mathrm{aquart}=\mathrm{1} \\ $$

Commented by a.lgnaoui last updated on 11/Jan/24

Commented by a.lgnaoui last updated on 11/Jan/24

Answered by Rasheed.Sindhi last updated on 13/Jan/24

Commented by Rasheed.Sindhi last updated on 13/Jan/24

Blue △: cos(25)=(a/c)=(a/1)⇒a=cos(25) sin(25)=(b/c) =(b/1)⇒b=sin(25) Blue▲=((ab)/2)=((cos(25)sin(25))/2) determinant (((Blue▲=((ab)/2)=m((cos(25)sin(25))/2)))) Green △: tan(25)=(d/c)=(d/1)⇒d=tan(25) ▲=(dc/2)=((tan(25)(1))/2)=((tan(25))/2) Green▲=(dc/2)=((tan(25))/2) determinant (((Green▲=(dc/2)=((tan(25))/2)))) Red △: angle between h & g=90−2(25)=40 cos(40)=(h/g)=(h/( (√(c^2 +d^2 ))))=(h/( (√(1+tan^2 (25))))) ⇒h=(√(1+tan^2 (25))) (cos(40)) sin(40)=(i/g)=(i/( (√(c^2 +d^2 )))) =(i/( (√(1+tan^2 (25))))) ⇒i=(√(1+tan^2 (25))) (sin(40)) ▲=((hi)/2)=(((√(1+tan^2 (25))) (cos(40))(√(1+tan^2 (25))) (sin(40)))/2) Red▲=((hi)/2)=(( (cos(40))(sin(40))(1+tan^2 (25)))/2) determinant ((( Red▲=((hi)/2)=(( (cos(40))(sin(40))(1+tan^2 (25)))/2)))) Green▲:Blue▲:Red▲ =((tan(25))/2):((cos(25)sin(25))/2):(( (cos(40))(sin(40))(1+tan^2 (25)))/2) =tan(25):cos(25)sin(25): (cos(40))(sin(40))(1+tan^2 (25))

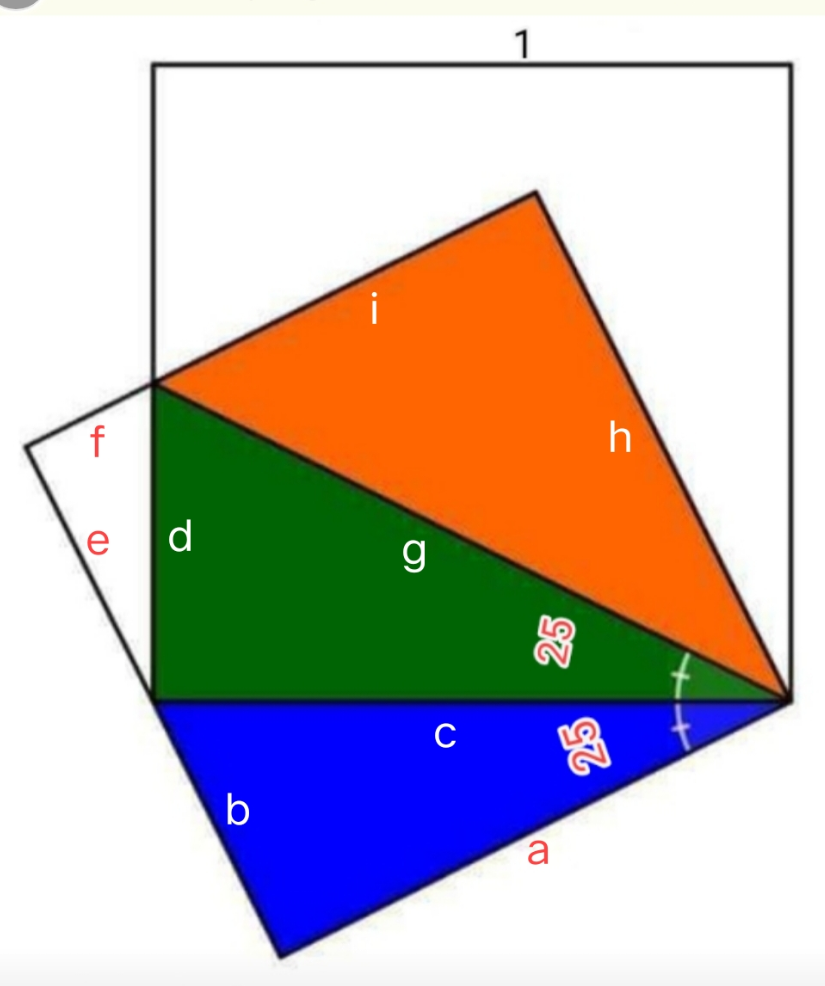
$$\mathrm{Blue}\:\bigtriangleup: \\ $$$$\:\:\:\mathrm{cos}\left(\mathrm{25}\right)=\frac{{a}}{{c}}=\frac{{a}}{\mathrm{1}}\Rightarrow{a}=\mathrm{cos}\left(\mathrm{25}\right) \\ $$$$\:\:\:\mathrm{sin}\left(\mathrm{25}\right)=\frac{{b}}{{c}}\:=\frac{{b}}{\mathrm{1}}\Rightarrow{b}=\mathrm{sin}\left(\mathrm{25}\right) \\ $$$$\:\:\:\mathrm{Blue}\blacktriangle=\frac{{ab}}{\mathrm{2}}=\frac{\mathrm{cos}\left(\mathrm{25}\right)\mathrm{sin}\left(\mathrm{25}\right)}{\mathrm{2}} \\ $$$$\begin{array}{|c|}{\mathrm{Blue}\blacktriangle=\frac{{ab}}{\mathrm{2}}={m}\frac{\mathrm{cos}\left(\mathrm{25}\right)\mathrm{sin}\left(\mathrm{25}\right)}{\mathrm{2}}}\\\hline\end{array} \\ $$$$\mathrm{Green}\:\bigtriangleup: \\ $$$$\:\:\mathrm{tan}\left(\mathrm{25}\right)=\frac{{d}}{{c}}=\frac{{d}}{\mathrm{1}}\Rightarrow{d}=\mathrm{tan}\left(\mathrm{25}\right) \\ $$$$\:\:\:\blacktriangle=\frac{{dc}}{\mathrm{2}}=\frac{\mathrm{tan}\left(\mathrm{25}\right)\left(\mathrm{1}\right)}{\mathrm{2}}=\frac{\mathrm{tan}\left(\mathrm{25}\right)}{\mathrm{2}} \\ $$$$\:\:\:\mathrm{Green}\blacktriangle=\frac{{dc}}{\mathrm{2}}=\frac{\mathrm{tan}\left(\mathrm{25}\right)}{\mathrm{2}}\: \\ $$$$\:\:\:\begin{array}{|c|}{\mathrm{Green}\blacktriangle=\frac{{dc}}{\mathrm{2}}=\frac{\mathrm{tan}\left(\mathrm{25}\right)}{\mathrm{2}}}\\\hline\end{array} \\ $$$$\mathrm{Red}\:\bigtriangleup: \\ $$$$\:\:\:\:\:{angle}\:{between}\:{h}\:\&\:{g}=\mathrm{90}−\mathrm{2}\left(\mathrm{25}\right)=\mathrm{40} \\ $$$$\:\:\:\:\mathrm{cos}\left(\mathrm{40}\right)=\frac{{h}}{{g}}=\frac{{h}}{\:\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }}=\frac{{h}}{\:\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{25}\right)}} \\ $$$$\:\:\:\:\:\Rightarrow{h}=\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{25}\right)}\:\left(\mathrm{cos}\left(\mathrm{40}\right)\right) \\ $$$$\:\:\:\:\:\mathrm{sin}\left(\mathrm{40}\right)=\frac{{i}}{{g}}=\frac{{i}}{\:\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }}\:=\frac{{i}}{\:\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{25}\right)}} \\ $$$$\:\:\:\:\:\:\Rightarrow{i}=\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{25}\right)}\:\left(\mathrm{sin}\left(\mathrm{40}\right)\right) \\ $$$$\:\:\:\:\:\:\blacktriangle=\frac{{hi}}{\mathrm{2}}=\frac{\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{25}\right)}\:\left(\mathrm{cos}\left(\mathrm{40}\right)\right)\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{25}\right)}\:\left(\mathrm{sin}\left(\mathrm{40}\right)\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\mathrm{Red}\blacktriangle=\frac{{hi}}{\mathrm{2}}=\frac{\:\left(\mathrm{cos}\left(\mathrm{40}\right)\right)\left(\mathrm{sin}\left(\mathrm{40}\right)\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{25}\right)\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\begin{array}{|c|}{\:\:\:\:\mathrm{Red}\blacktriangle=\frac{{hi}}{\mathrm{2}}=\frac{\:\left(\mathrm{cos}\left(\mathrm{40}\right)\right)\left(\mathrm{sin}\left(\mathrm{40}\right)\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{25}\right)\right)}{\mathrm{2}}}\\\hline\end{array} \\ $$$$\: \\ $$$$\mathrm{Green}\blacktriangle:\mathrm{Blue}\blacktriangle:\mathrm{Red}\blacktriangle \\ $$$$=\frac{\mathrm{tan}\left(\mathrm{25}\right)}{\mathrm{2}}:\frac{\mathrm{cos}\left(\mathrm{25}\right)\mathrm{sin}\left(\mathrm{25}\right)}{\mathrm{2}}:\frac{\:\left(\mathrm{cos}\left(\mathrm{40}\right)\right)\left(\mathrm{sin}\left(\mathrm{40}\right)\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{25}\right)\right)}{\mathrm{2}} \\ $$$$=\mathrm{tan}\left(\mathrm{25}\right):\mathrm{cos}\left(\mathrm{25}\right)\mathrm{sin}\left(\mathrm{25}\right):\:\left(\mathrm{cos}\left(\mathrm{40}\right)\right)\left(\mathrm{sin}\left(\mathrm{40}\right)\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{25}\right)\right) \\ $$

Commented by a.lgnaoui last updated on 13/Jan/24

Merci

$$\mathrm{Merci}\: \\ $$

Commented by a.lgnaoui last updated on 13/Jan/24

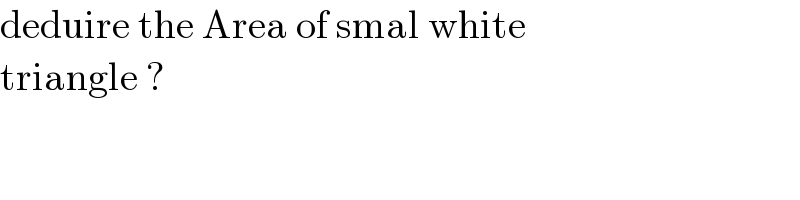
deduire the Area of smal white triangle ?

$$\mathrm{deduire}\:\mathrm{the}\:\mathrm{Area}\:\mathrm{of}\:\mathrm{smal}\:\mathrm{white} \\ $$$$\mathrm{triangle}\:? \\ $$

Commented by Rasheed.Sindhi last updated on 14/Jan/24

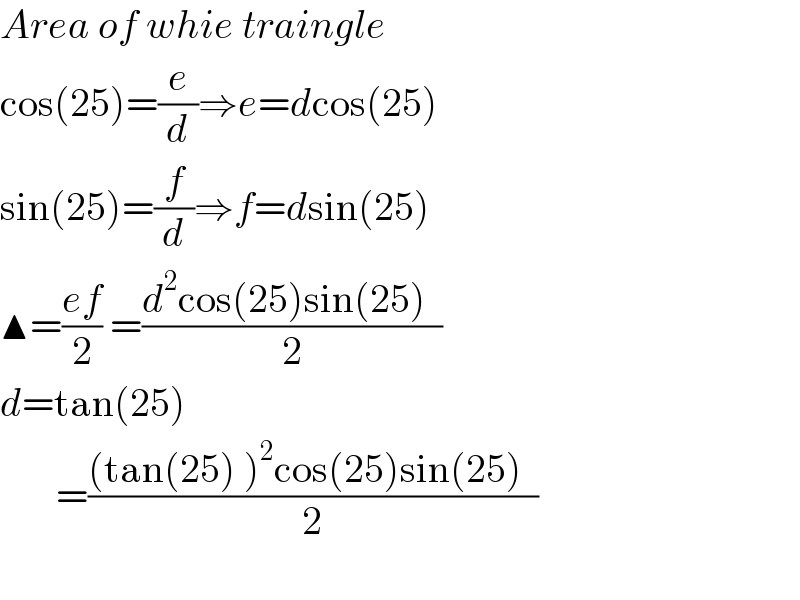
Area of whie traingle cos(25)=(e/d)⇒e=dcos(25) sin(25)=(f/d)⇒f=dsin(25) ▲=((ef)/2) =((d^2 cos(25)sin(25) )/2) d=tan(25) =(((tan(25) )^2 cos(25)sin(25) )/2)

$${Area}\:{of}\:{whie}\:{traingle} \\ $$$$\mathrm{cos}\left(\mathrm{25}\right)=\frac{{e}}{{d}}\Rightarrow{e}={d}\mathrm{cos}\left(\mathrm{25}\right)\: \\ $$$$\mathrm{sin}\left(\mathrm{25}\right)=\frac{{f}}{{d}}\Rightarrow{f}={d}\mathrm{sin}\left(\mathrm{25}\right) \\ $$$$\blacktriangle=\frac{{ef}}{\mathrm{2}}\:=\frac{{d}^{\mathrm{2}} \mathrm{cos}\left(\mathrm{25}\right)\mathrm{sin}\left(\mathrm{25}\right)\:\:}{\mathrm{2}}\: \\ $$$${d}=\mathrm{tan}\left(\mathrm{25}\right)\: \\ $$$$\:\:\:\:\:\:\:=\frac{\left(\mathrm{tan}\left(\mathrm{25}\right)\:\right)^{\mathrm{2}} \mathrm{cos}\left(\mathrm{25}\right)\mathrm{sin}\left(\mathrm{25}\right)\:\:}{\mathrm{2}}\: \\ $$$$ \\ $$

Commented by MathematicalUser2357 last updated on 20/Jan/24

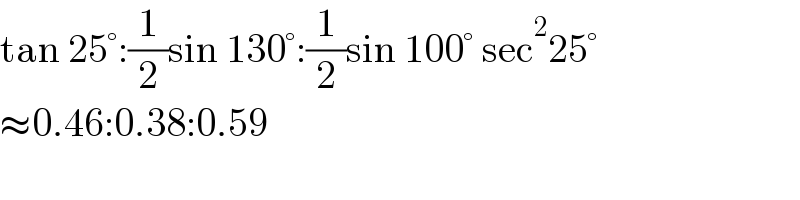
tan 25°:(1/2)sin 130°:(1/2)sin 100° sec^2 25° ≈0.46:0.38:0.59

$$\mathrm{tan}\:\mathrm{25}°:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{130}°:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{100}°\:\mathrm{sec}^{\mathrm{2}} \mathrm{25}° \\ $$$$\approx\mathrm{0}.\mathrm{46}:\mathrm{0}.\mathrm{38}:\mathrm{0}.\mathrm{59} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com