Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 203158 by hardmath last updated on 11/Jan/24

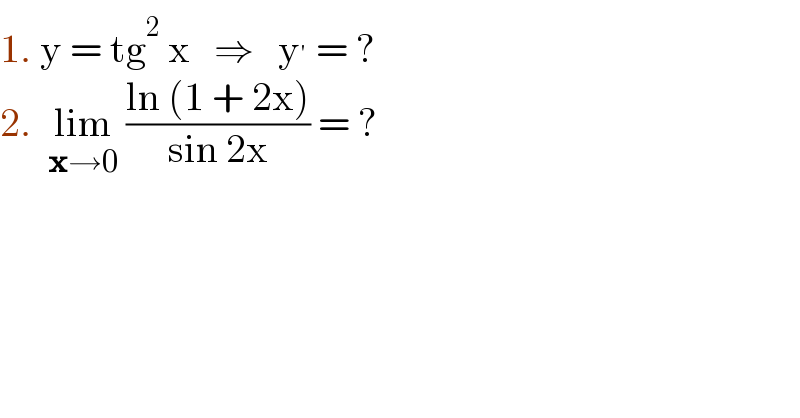
1. y = tg^2 x ⇒ y^′ = ? 2. lim_(x→0) ((ln (1 + 2x))/(sin 2x)) = ?

$$\mathrm{1}.\:\mathrm{y}\:=\:\mathrm{tg}^{\mathrm{2}} \:\mathrm{x}\:\:\:\Rightarrow\:\:\:\mathrm{y}^{'} \:=\:? \\ $$$$\mathrm{2}.\:\:\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\mathrm{1}\:+\:\mathrm{2x}\right)}{\mathrm{sin}\:\mathrm{2x}}\:=\:? \\ $$

Answered by shunmisaki007 last updated on 11/Jan/24

1. Are t, g, and x all variable or one or two of them constant? 2. Because lim_(x→0) ln(1+2x) = 0 and lim_(x→0) sin(2x) = 0, by L′hopital′s rule, lim_(x→0) ((ln(1+2x))/(sin(2x))) = lim_(x→0) (((d/dx)(ln(1+2x)))/((d/dx)(sin(2x)))) = lim_(x→0) ((2/(1+2x))/(2cos(2x))) = 1. ★

$$\mathrm{1}.\:\mathrm{Are}\:{t},\:{g},\:\mathrm{and}\:{x}\:\mathrm{all}\:\mathrm{variable}\:\mathrm{or}\:\mathrm{one}\:\mathrm{or}\:\mathrm{two}\:\mathrm{of}\:\mathrm{them}\:\mathrm{constant}? \\ $$$$\mathrm{2}.\:\mathrm{Because}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{ln}\left(\mathrm{1}+\mathrm{2}{x}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{and}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{sin}\left(\mathrm{2}{x}\right)\:=\:\mathrm{0}, \\ $$$$\mathrm{by}\:\mathrm{L}'\mathrm{hopital}'\mathrm{s}\:\mathrm{rule}, \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{2}{x}\right)}{\mathrm{sin}\left(\mathrm{2}{x}\right)}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{d}}{{dx}}\left(\mathrm{ln}\left(\mathrm{1}+\mathrm{2}{x}\right)\right)}{\frac{{d}}{{dx}}\left(\mathrm{sin}\left(\mathrm{2}{x}\right)\right)} \\ $$$$\:\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{2}}{\mathrm{1}+\mathrm{2}{x}}}{\mathrm{2cos}\left(\mathrm{2}{x}\right)} \\ $$$$\:\:\:=\:\mathrm{1}.\:\bigstar \\ $$

Commented by Frix last updated on 11/Jan/24

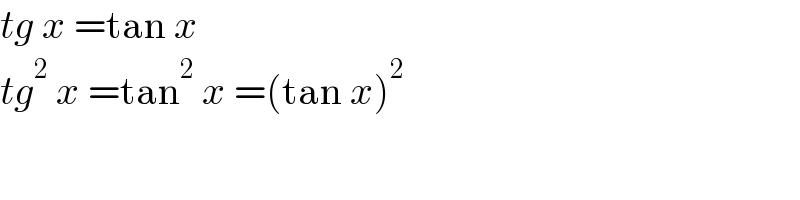
tg x =tan x tg^2 x =tan^2 x =(tan x)^2

$${tg}\:{x}\:=\mathrm{tan}\:{x} \\ $$$${tg}^{\mathrm{2}} \:{x}\:=\mathrm{tan}^{\mathrm{2}} \:{x}\:=\left(\mathrm{tan}\:{x}\right)^{\mathrm{2}} \\ $$

Answered by witcher3 last updated on 11/Jan/24

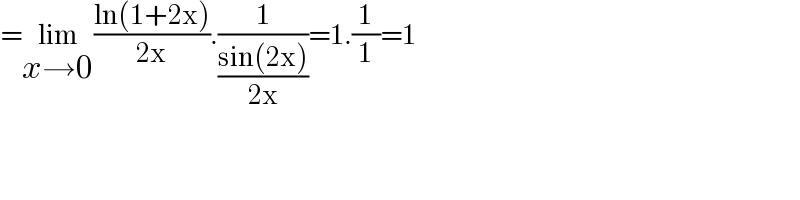
=lim_(x→0) ((ln(1+2x))/(2x)).(1/((sin(2x))/(2x)))=1.(1/1)=1

$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{2x}\right)}{\mathrm{2x}}.\frac{\mathrm{1}}{\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{2x}}}=\mathrm{1}.\frac{\mathrm{1}}{\mathrm{1}}=\mathrm{1} \\ $$

Answered by shunmisaki007 last updated on 11/Jan/24

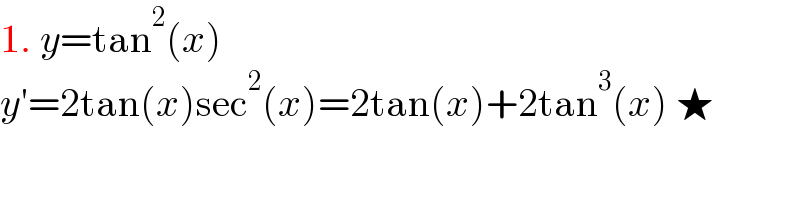
1. y=tan^2 (x) y′=2tan(x)sec^2 (x)=2tan(x)+2tan^3 (x) ★

$$\mathrm{1}.\:{y}=\mathrm{tan}^{\mathrm{2}} \left({x}\right) \\ $$$${y}'=\mathrm{2tan}\left({x}\right)\mathrm{sec}^{\mathrm{2}} \left({x}\right)=\mathrm{2tan}\left({x}\right)+\mathrm{2tan}^{\mathrm{3}} \left({x}\right)\:\bigstar \\ $$

Commented by Frix last updated on 11/Jan/24

��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com