
Question Number 202868 by hardmath last updated on 04/Jan/24
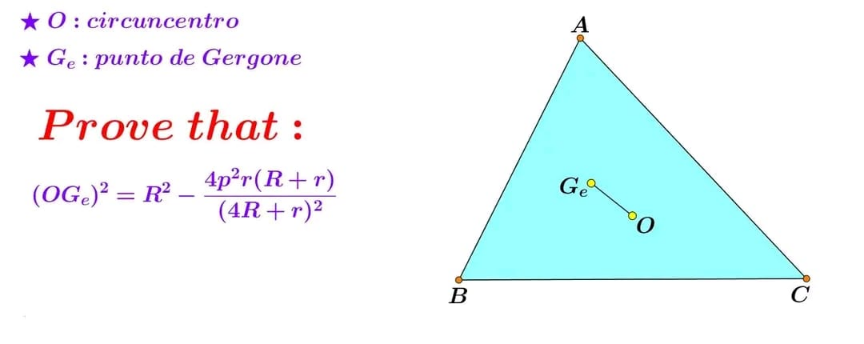
Commented by mr W last updated on 04/Jan/24
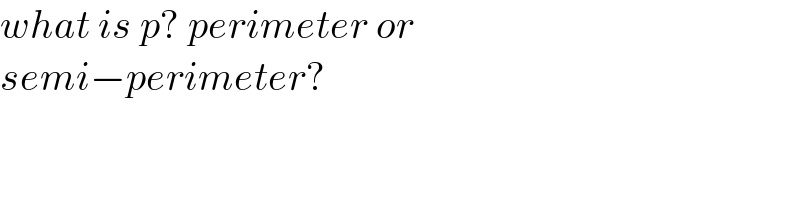
$${what}\:{is}\:{p}?\:{perimeter}\:{or}\: \\ $$$${semi}−{perimeter}? \\ $$
Commented by hardmath last updated on 04/Jan/24

$$\mathrm{My}\:\mathrm{dear}\:\mathrm{professor},\:\mathrm{semi}-\mathrm{perimeter} \\ $$
Answered by mr W last updated on 05/Jan/24
Commented by hardmath last updated on 05/Jan/24
$$\mathrm{My}\:\mathrm{darling}\:\mathrm{professor},\:\mathrm{you}\:\mathrm{are}\:\mathrm{perfect}... \\ $$
Commented by mr W last updated on 05/Jan/24
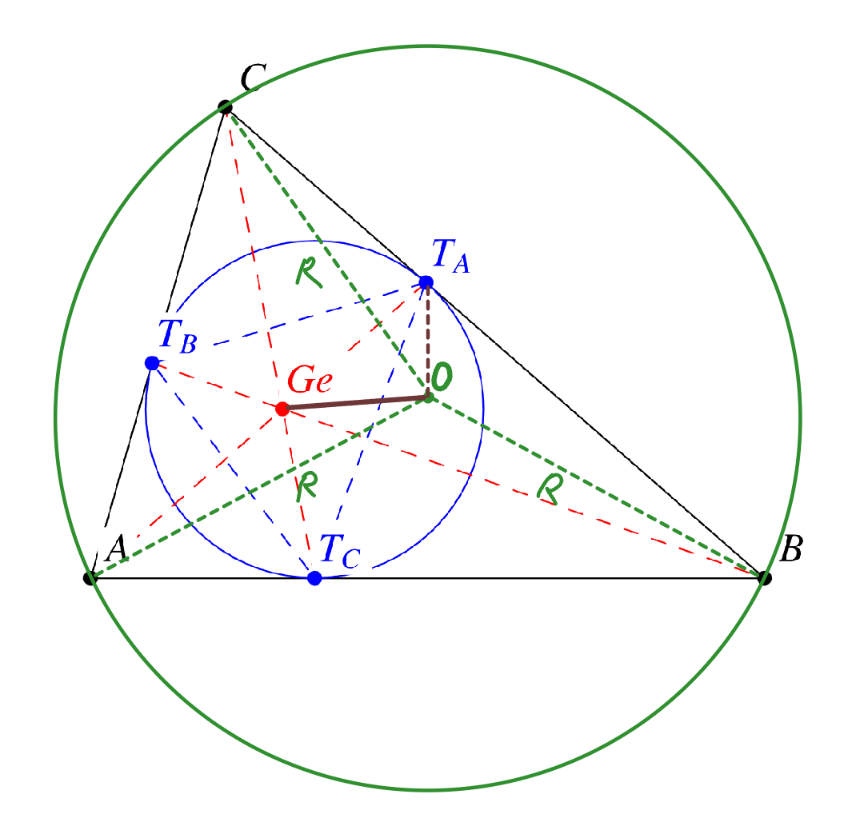
![p=((a+b+c)/2) AT_B =AT_C =p−a BT_A =BT_C =p−b CT_A =CT_B =p−c S=area of ΔABC =pr=((abc)/(4R))=(√(p(p−a)(p−b)(p−c))) in ΔABC: aAT_A ^2 =(p−b)b^2 +(p−c)c^2 −a(p−b)(p−c) AT_A ^2 =(((p−b)b^2 +(p−c)c^2 )/a)−(p−b)(p−c) AT_A ^2 =(((p−a)a^2 +(p−b)b^2 +(p−c)c^2 −abc)/a)+(p−a)^2 AT_A ^2 =((p(a^2 +b^2 +c^2 )−(a^3 +b^3 +c^3 )−abc)/a)+(p−a)^2 AT_A ^2 =((p(2p^2 −2r^2 −8Rr)−(2p^3 −6r^2 p−12Rrp)−abc)/a)+(p−a)^2 AT_A ^2 =((4r^2 p+4Rrp−abc)/a)+(p−a)^2 AT_A ^2 =((4pr^2 +4RS−4RS)/a)+(p−a)^2 AT_A ^2 =((4pr^2 )/a)+(p−a)^2 ⇒AT_A =(√(((4pr^2 )/a)+(p−a)^2 )) similarly BT_B =(√(((4pr^2 )/b)+(p−b)^2 )) CT_C =(√(((4pr^2 )/c)+(p−c)^2 )) ((AG_e )/(G_e T_A ))×((BT_A )/(BC))×((CT_B )/(T_B A))=1 ((AG_e )/(G_e T_A ))×((p−b)/a)×((p−c)/(p−a))=1 ⇒((AG_e )/(G_e T_A ))=((a(p−a))/((p−b)(p−c))) ⇒AG_e =((a(p−a))/(a(p−a)+(p−b)(p−c)))×AT_A =((4a(p−a))/(2(ab+bc+ca)−(a^2 +b^2 +c^2 )))×AT_A =((4a(p−a))/(2(p^2 +r^2 +4Rr)−(2p^2 −2r^2 −8Rr)))×AT_A =((a(p−a))/(r^2 +4Rr))×AT_A ⇒G_e T_A =(((p−b)(p−c))/(a(p−a)+(p−b)(p−c)))×AT_A =(((p−b)(p−c))/(r^2 +4Rr))×AT_A in ΔOBC: aOT_A ^2 =(p−b)R^2 +(p−c)R^2 −a(p−b)(p−c) ⇒OT_A ^2 =R^2 −(p−b)(p−c) in ΔOAT_A : AT_A ×OG_e ^2 =AG_e ×OT_A ^2 +G_e T_A ×OA^2 −AT_A ×AG_e ×G_e T_A OG_e ^2 =((AG_e )/(AT_A ))×OT_A ^2 +((G_e T_A )/(AT_A ))×OA^2 −AG_e ×G_e T_A OG_e ^2 =((a(p−a))/(r^2 +4Rr))×[R^2 −(p−b)(p−c)]+(((p−b)(p−c)R^2 )/(r^2 +4Rr))−((a(p−a))/(r^2 +4Rr))×(((p−b)(p−c))/(r^2 +4Rr))×AT_A ^2 OG_e ^2 =(([a(p−a)+(p−b)(p−c)]R^2 )/(r^2 +4Rr))−((a(p−a)(p−b)(p−c))/(r^2 +4Rr))−((a(p−a)(p−b)(p−c))/((r^2 +4Rr)^2 ))×AT_A ^2 OG_e ^2 =(((r^2 +4Rr)R^2 )/(r^2 +4Rr))−((aS^2 )/((r^2 +4Rr)p))−((aS^2 )/((r^2 +4Rr)^2 p))×AT_A ^2 OG_e ^2 =R^2 −((aS^2 )/((r^2 +4Rr)^2 p))(r^2 +4Rr+AT_A ^2 ) OG_e ^2 =R^2 −((apr^2 )/((r^2 +4Rr)^2 ))[r^2 +4Rr+((4pr^2 )/a)+(p−a)^2 ] OG_e ^2 =R^2 −((ap)/((r+4R)^2 ))(p^2 +r^2 +4Rr+((4pr^2 )/a)+a^2 −2pa) OG_e ^2 =R^2 −((ap)/((r+4R)^2 ))(ab+bc+ca+((4pr^2 )/a)+a^2 −a^2 −ab−ca) OG_e ^2 =R^2 −((ap)/((r+4R)^2 ))(bc+((4pr^2 )/a)) OG_e ^2 =R^2 −(p/((r+4)^2 ))(abc+4pr^2 ) OG_e ^2 =R^2 −(p/((r+4R)^2 ))(4Rpr+4pr^2 ) OG_e ^2 =R^2 −((4p^2 r(R+r))/((4R+r)^2 )) ✓](Q202910.png)
$${p}=\frac{{a}+{b}+{c}}{\mathrm{2}} \\ $$$${AT}_{{B}} ={AT}_{{C}} ={p}−{a} \\ $$$${BT}_{{A}} ={BT}_{{C}} ={p}−{b} \\ $$$${CT}_{{A}} ={CT}_{{B}} ={p}−{c} \\ $$$${S}={area}\:{of}\:\Delta{ABC} \\ $$$$\:\:\:={pr}=\frac{{abc}}{\mathrm{4}{R}}=\sqrt{{p}\left({p}−{a}\right)\left({p}−{b}\right)\left({p}−{c}\right)} \\ $$$$ \\ $$$${in}\:\Delta{ABC}: \\ $$$${aAT}_{{A}} ^{\mathrm{2}} =\left({p}−{b}\right){b}^{\mathrm{2}} +\left({p}−{c}\right){c}^{\mathrm{2}} −{a}\left({p}−{b}\right)\left({p}−{c}\right) \\ $$$${AT}_{{A}} ^{\mathrm{2}} =\frac{\left({p}−{b}\right){b}^{\mathrm{2}} +\left({p}−{c}\right){c}^{\mathrm{2}} }{{a}}−\left({p}−{b}\right)\left({p}−{c}\right) \\ $$$${AT}_{{A}} ^{\mathrm{2}} =\frac{\left({p}−{a}\right){a}^{\mathrm{2}} +\left({p}−{b}\right){b}^{\mathrm{2}} +\left({p}−{c}\right){c}^{\mathrm{2}} −{abc}}{{a}}+\left({p}−{a}\right)^{\mathrm{2}} \\ $$$${AT}_{{A}} ^{\mathrm{2}} =\frac{{p}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \right)−{abc}}{{a}}+\left({p}−{a}\right)^{\mathrm{2}} \\ $$$${AT}_{{A}} ^{\mathrm{2}} =\frac{{p}\left(\mathrm{2}{p}^{\mathrm{2}} −\mathrm{2}{r}^{\mathrm{2}} −\mathrm{8}{Rr}\right)−\left(\mathrm{2}{p}^{\mathrm{3}} −\mathrm{6}{r}^{\mathrm{2}} {p}−\mathrm{12}{Rrp}\right)−{abc}}{{a}}+\left({p}−{a}\right)^{\mathrm{2}} \\ $$$${AT}_{{A}} ^{\mathrm{2}} =\frac{\mathrm{4}{r}^{\mathrm{2}} {p}+\mathrm{4}{Rrp}−{abc}}{{a}}+\left({p}−{a}\right)^{\mathrm{2}} \\ $$$${AT}_{{A}} ^{\mathrm{2}} =\frac{\mathrm{4}{pr}^{\mathrm{2}} +\mathrm{4}{RS}−\mathrm{4}{RS}}{{a}}+\left({p}−{a}\right)^{\mathrm{2}} \\ $$$${AT}_{{A}} ^{\mathrm{2}} =\frac{\mathrm{4}{pr}^{\mathrm{2}} }{{a}}+\left({p}−{a}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{AT}_{{A}} =\sqrt{\frac{\mathrm{4}{pr}^{\mathrm{2}} }{{a}}+\left({p}−{a}\right)^{\mathrm{2}} } \\ $$$${similarly} \\ $$$${BT}_{{B}} =\sqrt{\frac{\mathrm{4}{pr}^{\mathrm{2}} }{{b}}+\left({p}−{b}\right)^{\mathrm{2}} } \\ $$$${CT}_{{C}} =\sqrt{\frac{\mathrm{4}{pr}^{\mathrm{2}} }{{c}}+\left({p}−{c}\right)^{\mathrm{2}} } \\ $$$$\frac{{AG}_{{e}} }{{G}_{{e}} {T}_{{A}} }×\frac{{BT}_{{A}} }{{BC}}×\frac{{CT}_{{B}} }{{T}_{{B}} {A}}=\mathrm{1} \\ $$$$\frac{{AG}_{{e}} }{{G}_{{e}} {T}_{{A}} }×\frac{{p}−{b}}{{a}}×\frac{{p}−{c}}{{p}−{a}}=\mathrm{1} \\ $$$$\Rightarrow\frac{{AG}_{{e}} }{{G}_{{e}} {T}_{{A}} }=\frac{{a}\left({p}−{a}\right)}{\left({p}−{b}\right)\left({p}−{c}\right)} \\ $$$$\Rightarrow{AG}_{{e}} =\frac{{a}\left({p}−{a}\right)}{{a}\left({p}−{a}\right)+\left({p}−{b}\right)\left({p}−{c}\right)}×{AT}_{{A}} \\ $$$$\:\:\:\:=\frac{\mathrm{4}{a}\left({p}−{a}\right)}{\mathrm{2}\left({ab}+{bc}+{ca}\right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)}×{AT}_{{A}} \\ $$$$\:\:\:\:=\frac{\mathrm{4}{a}\left({p}−{a}\right)}{\mathrm{2}\left({p}^{\mathrm{2}} +{r}^{\mathrm{2}} +\mathrm{4}{Rr}\right)−\left(\mathrm{2}{p}^{\mathrm{2}} −\mathrm{2}{r}^{\mathrm{2}} −\mathrm{8}{Rr}\right)}×{AT}_{{A}} \\ $$$$\:\:\:\:=\frac{{a}\left({p}−{a}\right)}{{r}^{\mathrm{2}} +\mathrm{4}{Rr}}×{AT}_{{A}} \\ $$$$\Rightarrow{G}_{{e}} {T}_{{A}} =\frac{\left({p}−{b}\right)\left({p}−{c}\right)}{{a}\left({p}−{a}\right)+\left({p}−{b}\right)\left({p}−{c}\right)}×{AT}_{{A}} \\ $$$$\:\:\:\:=\frac{\left({p}−{b}\right)\left({p}−{c}\right)}{{r}^{\mathrm{2}} +\mathrm{4}{Rr}}×{AT}_{{A}} \\ $$$$ \\ $$$${in}\:\Delta{OBC}: \\ $$$${aOT}_{{A}} ^{\mathrm{2}} =\left({p}−{b}\right){R}^{\mathrm{2}} +\left({p}−{c}\right){R}^{\mathrm{2}} −{a}\left({p}−{b}\right)\left({p}−{c}\right) \\ $$$$\Rightarrow{OT}_{{A}} ^{\mathrm{2}} ={R}^{\mathrm{2}} −\left({p}−{b}\right)\left({p}−{c}\right) \\ $$$$ \\ $$$${in}\:\Delta{OAT}_{{A}} : \\ $$$${AT}_{{A}} ×{OG}_{{e}} ^{\mathrm{2}} ={AG}_{{e}} ×{OT}_{{A}} ^{\mathrm{2}} +{G}_{{e}} {T}_{{A}} ×{OA}^{\mathrm{2}} −{AT}_{{A}} ×{AG}_{{e}} ×{G}_{{e}} {T}_{{A}} \\ $$$${OG}_{{e}} ^{\mathrm{2}} =\frac{{AG}_{{e}} }{{AT}_{{A}} }×{OT}_{{A}} ^{\mathrm{2}} +\frac{{G}_{{e}} {T}_{{A}} }{{AT}_{{A}} }×{OA}^{\mathrm{2}} −{AG}_{{e}} ×{G}_{{e}} {T}_{{A}} \\ $$$${OG}_{{e}} ^{\mathrm{2}} =\frac{{a}\left({p}−{a}\right)}{{r}^{\mathrm{2}} +\mathrm{4}{Rr}}×\left[{R}^{\mathrm{2}} −\left({p}−{b}\right)\left({p}−{c}\right)\right]+\frac{\left({p}−{b}\right)\left({p}−{c}\right){R}^{\mathrm{2}} }{{r}^{\mathrm{2}} +\mathrm{4}{Rr}}−\frac{{a}\left({p}−{a}\right)}{{r}^{\mathrm{2}} +\mathrm{4}{Rr}}×\frac{\left({p}−{b}\right)\left({p}−{c}\right)}{{r}^{\mathrm{2}} +\mathrm{4}{Rr}}×{AT}_{{A}} ^{\mathrm{2}} \\ $$$${OG}_{{e}} ^{\mathrm{2}} =\frac{\left[{a}\left({p}−{a}\right)+\left({p}−{b}\right)\left({p}−{c}\right)\right]{R}^{\mathrm{2}} }{{r}^{\mathrm{2}} +\mathrm{4}{Rr}}−\frac{{a}\left({p}−{a}\right)\left({p}−{b}\right)\left({p}−{c}\right)}{{r}^{\mathrm{2}} +\mathrm{4}{Rr}}−\frac{{a}\left({p}−{a}\right)\left({p}−{b}\right)\left({p}−{c}\right)}{\left({r}^{\mathrm{2}} +\mathrm{4}{Rr}\right)^{\mathrm{2}} }×{AT}_{{A}} ^{\mathrm{2}} \\ $$$${OG}_{{e}} ^{\mathrm{2}} =\frac{\left({r}^{\mathrm{2}} +\mathrm{4}{Rr}\right){R}^{\mathrm{2}} }{{r}^{\mathrm{2}} +\mathrm{4}{Rr}}−\frac{{aS}^{\mathrm{2}} }{\left({r}^{\mathrm{2}} +\mathrm{4}{Rr}\right){p}}−\frac{{aS}^{\mathrm{2}} }{\left({r}^{\mathrm{2}} +\mathrm{4}{Rr}\right)^{\mathrm{2}} {p}}×{AT}_{{A}} ^{\mathrm{2}} \\ $$$${OG}_{{e}} ^{\mathrm{2}} ={R}^{\mathrm{2}} −\frac{{aS}^{\mathrm{2}} }{\left({r}^{\mathrm{2}} +\mathrm{4}{Rr}\right)^{\mathrm{2}} {p}}\left({r}^{\mathrm{2}} +\mathrm{4}{Rr}+{AT}_{{A}} ^{\mathrm{2}} \right) \\ $$$${OG}_{{e}} ^{\mathrm{2}} ={R}^{\mathrm{2}} −\frac{{apr}^{\mathrm{2}} }{\left({r}^{\mathrm{2}} +\mathrm{4}{Rr}\right)^{\mathrm{2}} }\left[{r}^{\mathrm{2}} +\mathrm{4}{Rr}+\frac{\mathrm{4}{pr}^{\mathrm{2}} }{{a}}+\left({p}−{a}\right)^{\mathrm{2}} \right] \\ $$$${OG}_{{e}} ^{\mathrm{2}} ={R}^{\mathrm{2}} −\frac{{ap}}{\left({r}+\mathrm{4}{R}\right)^{\mathrm{2}} }\left({p}^{\mathrm{2}} +{r}^{\mathrm{2}} +\mathrm{4}{Rr}+\frac{\mathrm{4}{pr}^{\mathrm{2}} }{{a}}+{a}^{\mathrm{2}} −\mathrm{2}{pa}\right) \\ $$$${OG}_{{e}} ^{\mathrm{2}} ={R}^{\mathrm{2}} −\frac{{ap}}{\left({r}+\mathrm{4}{R}\right)^{\mathrm{2}} }\left({ab}+{bc}+{ca}+\frac{\mathrm{4}{pr}^{\mathrm{2}} }{{a}}+{a}^{\mathrm{2}} −{a}^{\mathrm{2}} −{ab}−{ca}\right) \\ $$$${OG}_{{e}} ^{\mathrm{2}} ={R}^{\mathrm{2}} −\frac{{ap}}{\left({r}+\mathrm{4}{R}\right)^{\mathrm{2}} }\left({bc}+\frac{\mathrm{4}{pr}^{\mathrm{2}} }{{a}}\right) \\ $$$${OG}_{{e}} ^{\mathrm{2}} ={R}^{\mathrm{2}} −\frac{{p}}{\left({r}+\mathrm{4}\right)^{\mathrm{2}} }\left({abc}+\mathrm{4}{pr}^{\mathrm{2}} \right) \\ $$$${OG}_{{e}} ^{\mathrm{2}} ={R}^{\mathrm{2}} −\frac{{p}}{\left({r}+\mathrm{4}{R}\right)^{\mathrm{2}} }\left(\mathrm{4}{Rpr}+\mathrm{4}{pr}^{\mathrm{2}} \right) \\ $$$${OG}_{{e}} ^{\mathrm{2}} ={R}^{\mathrm{2}} −\frac{\mathrm{4}{p}^{\mathrm{2}} {r}\left({R}+{r}\right)}{\left(\mathrm{4}{R}+{r}\right)^{\mathrm{2}} }\:\checkmark \\ $$
Commented by hardmath last updated on 05/Jan/24

$$\mathrm{My}\:\mathrm{darling}\:\mathrm{professor},\:\mathrm{this}\:\mathrm{is}\:\mathrm{excellent} \\ $$$$\mathrm{evidence},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}... \\ $$
