Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 202392 by MATHEMATICSAM last updated on 26/Dec/23

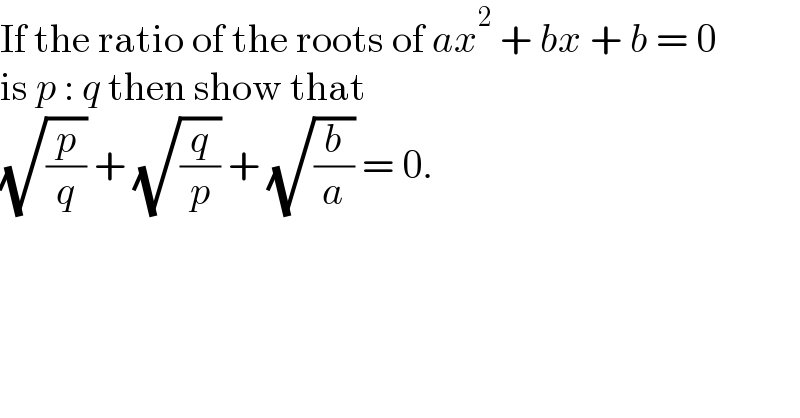
If the ratio of the roots of ax^2 + bx + b = 0 is p : q then show that (√(p/q)) + (√(q/p)) + (√(b/a)) = 0.

$$\mathrm{If}\:\mathrm{the}\:\mathrm{ratio}\:\mathrm{of}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:{ax}^{\mathrm{2}} \:+\:{bx}\:+\:{b}\:=\:\mathrm{0} \\ $$$$\mathrm{is}\:{p}\::\:{q}\:\mathrm{then}\:\mathrm{show}\:\mathrm{that} \\ $$$$\sqrt{\frac{{p}}{{q}}}\:+\:\sqrt{\frac{{q}}{{p}}}\:+\:\sqrt{\frac{{b}}{{a}}}\:=\:\mathrm{0}. \\ $$

Commented by MATHEMATICSAM last updated on 26/Dec/23

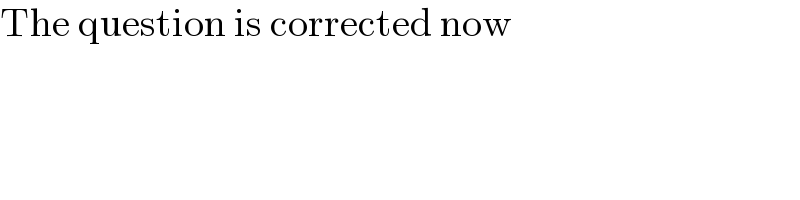
The question is corrected now

$$\mathrm{The}\:\mathrm{question}\:\mathrm{is}\:\mathrm{corrected}\:\mathrm{now} \\ $$

Commented by Frix last updated on 27/Dec/23

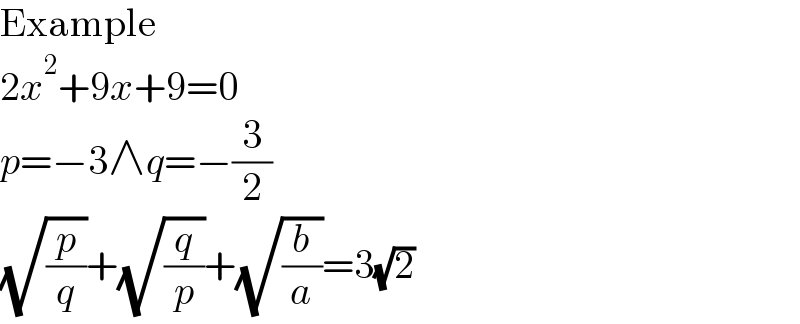
Example 2x^2 +9x+9=0 p=−3∧q=−(3/2) (√(p/q))+(√(q/p))+(√(b/a))=3(√2)

$$\mathrm{Example} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{9}{x}+\mathrm{9}=\mathrm{0} \\ $$$${p}=−\mathrm{3}\wedge{q}=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\sqrt{\frac{{p}}{{q}}}+\sqrt{\frac{{q}}{{p}}}+\sqrt{\frac{{b}}{{a}}}=\mathrm{3}\sqrt{\mathrm{2}} \\ $$

Commented by MATHEMATICSAM last updated on 27/Dec/23

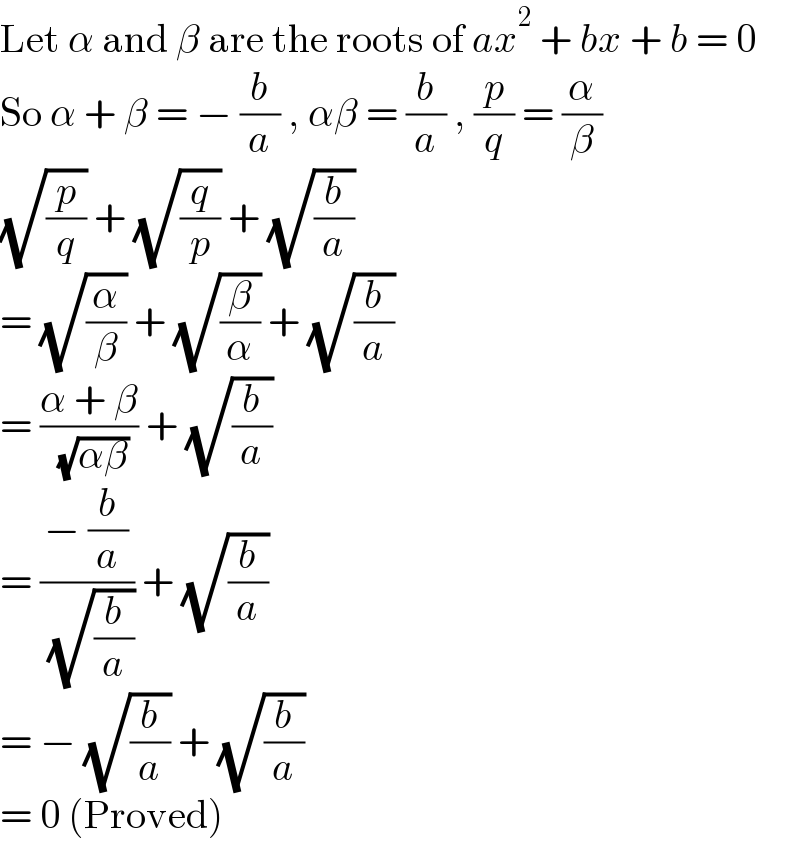
Let α and β are the roots of ax^2 + bx + b = 0 So α + β = − (b/a) , αβ = (b/a) , (p/q) = (α/β) (√(p/q)) + (√(q/p)) + (√(b/a)) = (√(α/β)) + (√(β/α)) + (√(b/a)) = ((α + β)/( (√(αβ)))) + (√(b/a)) = ((− (b/a))/( (√(b/a)))) + (√(b/a)) = − (√(b/a)) + (√(b/a)) = 0 (Proved)

$$\mathrm{Let}\:\alpha\:\mathrm{and}\:\beta\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:{ax}^{\mathrm{2}} \:+\:{bx}\:+\:{b}\:=\:\mathrm{0} \\ $$$$\mathrm{So}\:\alpha\:+\:\beta\:=\:−\:\frac{{b}}{{a}}\:,\:\alpha\beta\:=\:\frac{{b}}{{a}}\:,\:\frac{{p}}{{q}}\:=\:\frac{\alpha}{\beta} \\ $$$$\sqrt{\frac{{p}}{{q}}}\:+\:\sqrt{\frac{{q}}{{p}}}\:+\:\sqrt{\frac{{b}}{{a}}}\: \\ $$$$=\:\sqrt{\frac{\alpha}{\beta}}\:+\:\sqrt{\frac{\beta}{\alpha}}\:+\:\sqrt{\frac{{b}}{{a}}} \\ $$$$=\:\frac{\alpha\:+\:\beta}{\:\sqrt{\alpha\beta}}\:+\:\sqrt{\frac{{b}}{{a}}} \\ $$$$=\:\frac{−\:\frac{{b}}{{a}}}{\:\sqrt{\frac{{b}}{{a}}}}\:+\:\sqrt{\frac{{b}}{{a}}} \\ $$$$=\:−\:\sqrt{\frac{{b}}{{a}}}\:+\:\sqrt{\frac{{b}}{{a}}} \\ $$$$=\:\mathrm{0}\:\left(\mathrm{Proved}\right) \\ $$

Commented by MATHEMATICSAM last updated on 27/Dec/23

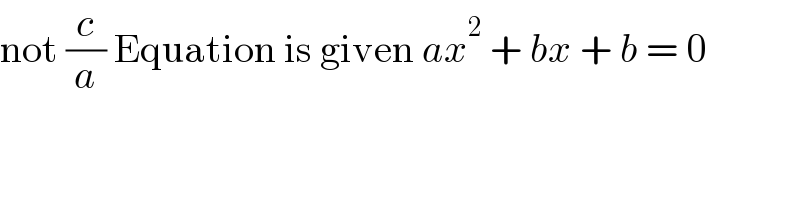
not (c/a) Equation is given ax^2 + bx + b = 0

$$\mathrm{not}\:\frac{{c}}{{a}}\:\mathrm{Equation}\:\mathrm{is}\:\mathrm{given}\:{ax}^{\mathrm{2}} \:+\:{bx}\:+\:{b}\:=\:\mathrm{0} \\ $$

Commented by Rasheed.Sindhi last updated on 27/Dec/23

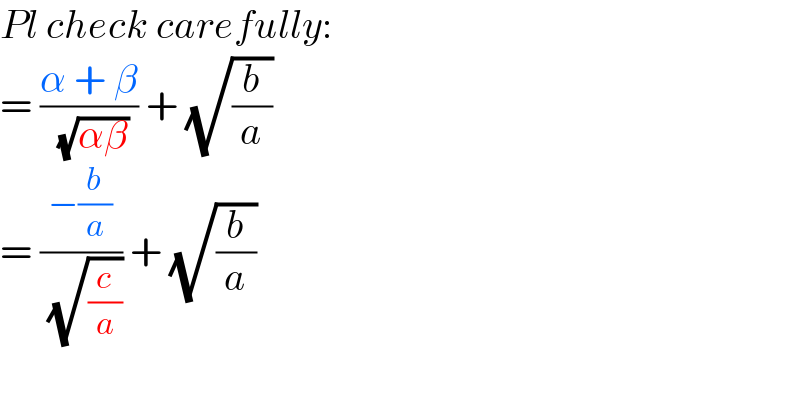
Pl check carefully: = ((α + β)/( (√(αβ)))) + (√(b/a)) = ((−(b/a))/( (√(c/a)))) + (√(b/a))

$${Pl}\:{check}\:{carefully}: \\ $$$$=\:\frac{\alpha\:+\:\beta}{\:\sqrt{\alpha\beta}}\:+\:\sqrt{\frac{{b}}{{a}}}\: \\ $$$$=\:\frac{−\frac{{b}}{{a}}}{\:\sqrt{\frac{{c}}{{a}}}}\:+\:\sqrt{\frac{{b}}{{a}}} \\ $$$$ \\ $$

Commented by Rasheed.Sindhi last updated on 27/Dec/23

Ok

$${Ok} \\ $$

Commented by Frix last updated on 27/Dec/23

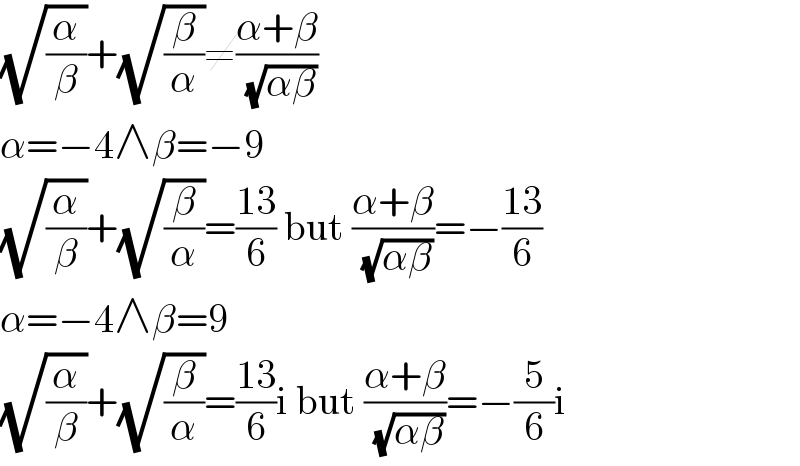
(√(α/β))+(√(β/α))≠((α+β)/( (√(αβ)))) α=−4∧β=−9 (√(α/β))+(√(β/α))=((13)/6) but ((α+β)/( (√(αβ))))=−((13)/6) α=−4∧β=9 (√(α/β))+(√(β/α))=((13)/6)i but ((α+β)/( (√(αβ))))=−(5/6)i

$$\sqrt{\frac{\alpha}{\beta}}+\sqrt{\frac{\beta}{\alpha}}\neq\frac{\alpha+\beta}{\:\sqrt{\alpha\beta}} \\ $$$$\alpha=−\mathrm{4}\wedge\beta=−\mathrm{9} \\ $$$$\sqrt{\frac{\alpha}{\beta}}+\sqrt{\frac{\beta}{\alpha}}=\frac{\mathrm{13}}{\mathrm{6}}\:\mathrm{but}\:\frac{\alpha+\beta}{\:\sqrt{\alpha\beta}}=−\frac{\mathrm{13}}{\mathrm{6}} \\ $$$$\alpha=−\mathrm{4}\wedge\beta=\mathrm{9} \\ $$$$\sqrt{\frac{\alpha}{\beta}}+\sqrt{\frac{\beta}{\alpha}}=\frac{\mathrm{13}}{\mathrm{6}}\mathrm{i}\:\mathrm{but}\:\frac{\alpha+\beta}{\:\sqrt{\alpha\beta}}=−\frac{\mathrm{5}}{\mathrm{6}}\mathrm{i} \\ $$

Commented by Frix last updated on 27/Dec/23

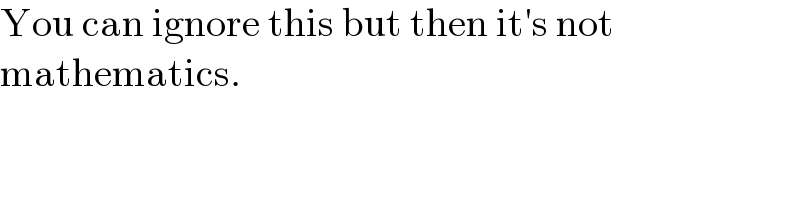
You can ignore this but then it′s not mathematics.

$$\mathrm{You}\:\mathrm{can}\:\mathrm{ignore}\:\mathrm{this}\:\mathrm{but}\:\mathrm{then}\:\mathrm{it}'\mathrm{s}\:\mathrm{not} \\ $$$$\mathrm{mathematics}. \\ $$

Commented by Rasheed.Sindhi last updated on 27/Dec/23

Sir, you′re very right!

$$\boldsymbol{\mathrm{Sir}},\:\mathrm{you}'\mathrm{re}\:\mathrm{very}\:\mathrm{right}! \\ $$

Commented by MATHEMATICSAM last updated on 27/Dec/23

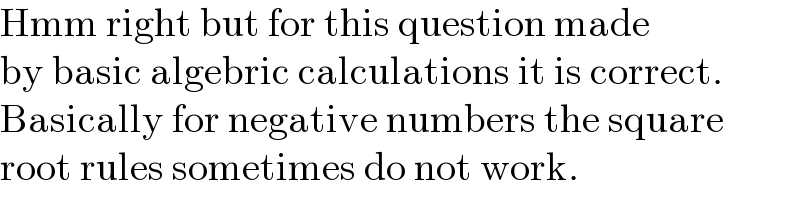
Hmm right but for this question made by basic algebric calculations it is correct. Basically for negative numbers the square root rules sometimes do not work.

$$\mathrm{Hmm}\:\mathrm{right}\:\mathrm{but}\:\mathrm{for}\:\mathrm{this}\:\mathrm{question}\:\mathrm{made} \\ $$$$\mathrm{by}\:\mathrm{basic}\:\mathrm{algebric}\:\mathrm{calculations}\:\mathrm{it}\:\mathrm{is}\:\mathrm{correct}. \\ $$$$\mathrm{Basically}\:\mathrm{for}\:\mathrm{negative}\:\mathrm{numbers}\:\mathrm{the}\:\mathrm{square} \\ $$$$\mathrm{root}\:\mathrm{rules}\:\mathrm{sometimes}\:\mathrm{do}\:\mathrm{not}\:\mathrm{work}. \\ $$

Commented by Frix last updated on 27/Dec/23

If it′s wrong it′s wrong. You′d have to restrict the values to get a valid solution.

$$\mathrm{If}\:\mathrm{it}'\mathrm{s}\:\mathrm{wrong}\:\mathrm{it}'\mathrm{s}\:\mathrm{wrong}. \\ $$$$\mathrm{You}'\mathrm{d}\:\mathrm{have}\:\mathrm{to}\:\mathrm{restrict}\:\mathrm{the}\:\mathrm{values}\:\mathrm{to}\:\mathrm{get} \\ $$$$\mathrm{a}\:\mathrm{valid}\:\mathrm{solution}. \\ $$

Answered by Rasheed.Sindhi last updated on 27/Dec/23

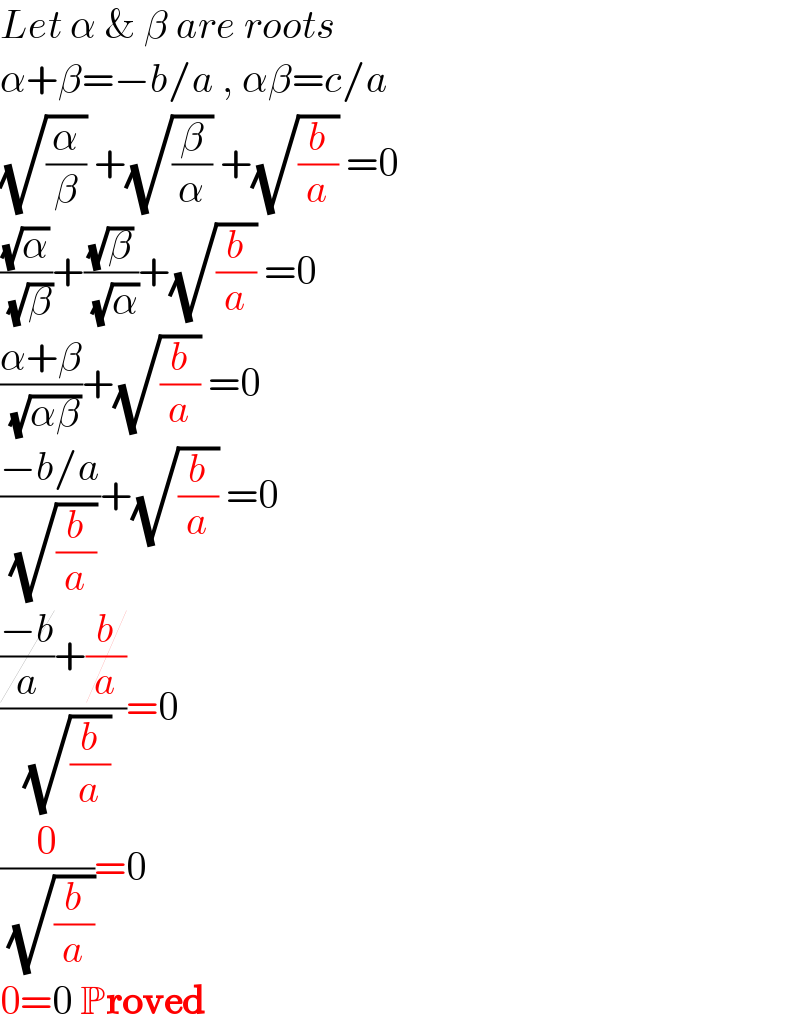
Let α & β are roots α+β=−b/a , αβ=c/a (√(α/β)) +(√(β/α)) +(√(b/a)) =0 ((√α)/( (√β)))+((√β)/( (√α)))+(√(b/a)) =0 ((α+β)/( (√(αβ))))+(√(b/a)) =0 ((−b/a)/( (√(b/a))))+(√(b/a)) =0 ((((−b)/a)+(b/a))/( (√(b/a))))=0 (0/( (√(b/a))))=0 0=0 Proved

$${Let}\:\alpha\:\&\:\beta\:{are}\:{roots} \\ $$$$\alpha+\beta=−{b}/{a}\:,\:\alpha\beta={c}/{a} \\ $$$$\sqrt{\frac{\alpha}{\beta}}\:+\sqrt{\frac{\beta}{\alpha}}\:+\sqrt{\frac{{b}}{{a}}}\:=\mathrm{0} \\ $$$$\frac{\sqrt{\alpha}}{\:\sqrt{\beta}}+\frac{\sqrt{\beta}}{\:\sqrt{\alpha}}+\sqrt{\frac{{b}}{{a}}}\:=\mathrm{0} \\ $$$$\frac{\alpha+\beta}{\:\sqrt{\alpha\beta}}+\sqrt{\frac{{b}}{{a}}}\:=\mathrm{0} \\ $$$$\frac{−{b}/{a}}{\:\sqrt{\frac{{b}}{{a}}}}+\sqrt{\frac{{b}}{{a}}}\:=\mathrm{0} \\ $$$$\frac{\cancel{\frac{−{b}}{{a}}}+\cancel{\frac{{b}}{{a}}}}{\:\sqrt{\frac{{b}}{{a}}}}=\mathrm{0} \\ $$$$\frac{\mathrm{0}}{\:\sqrt{\frac{{b}}{{a}}}}=\mathrm{0} \\ $$$$\mathrm{0}=\mathrm{0}\:\mathbb{P}\boldsymbol{\mathrm{roved}} \\ $$

Answered by Frix last updated on 26/Dec/23

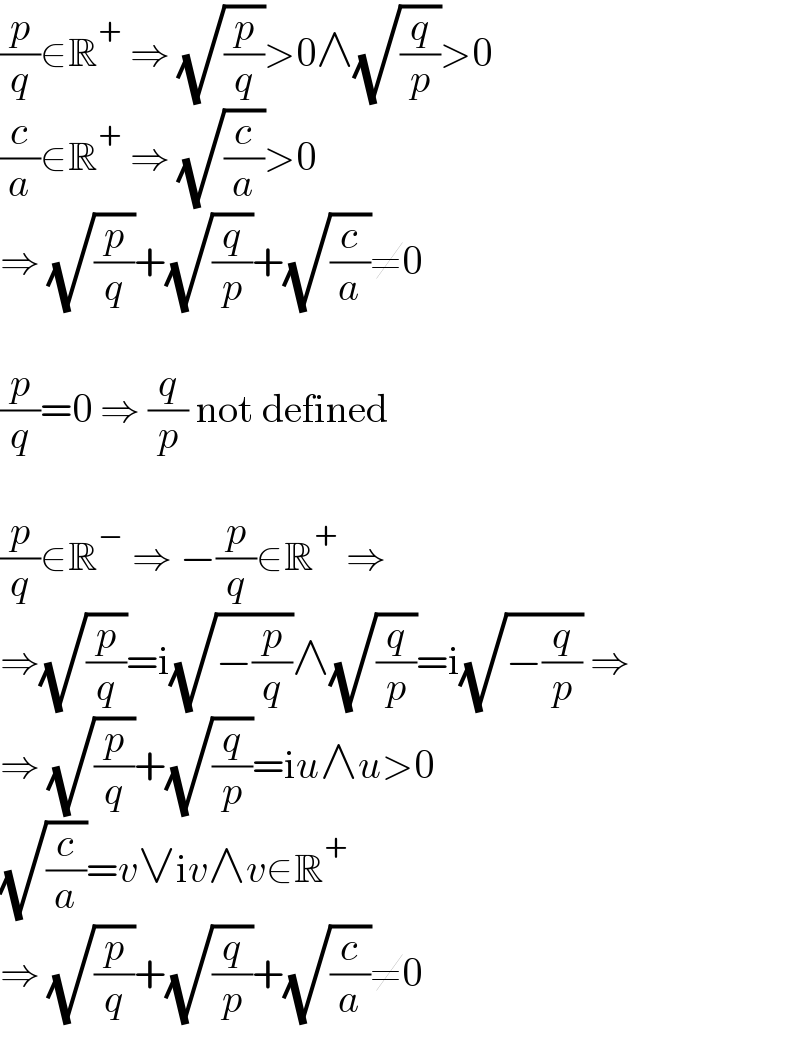
(p/q)∈R^+ ⇒ (√(p/q))>0∧(√(q/p))>0 (c/a)∈R^+ ⇒ (√(c/a))>0 ⇒ (√(p/q))+(√(q/p))+(√(c/a))≠0 (p/q)=0 ⇒ (q/p) not defined (p/q)∈R^− ⇒ −(p/q)∈R^+ ⇒ ⇒(√(p/q))=i(√(−(p/q)))∧(√(q/p))=i(√(−(q/p))) ⇒ ⇒ (√(p/q))+(√(q/p))=iu∧u>0 (√(c/a))=v∨iv∧v∈R^+ ⇒ (√(p/q))+(√(q/p))+(√(c/a))≠0

$$\frac{{p}}{{q}}\in\mathbb{R}^{+} \:\Rightarrow\:\sqrt{\frac{{p}}{{q}}}>\mathrm{0}\wedge\sqrt{\frac{{q}}{{p}}}>\mathrm{0} \\ $$$$\frac{{c}}{{a}}\in\mathbb{R}^{+} \:\Rightarrow\:\sqrt{\frac{{c}}{{a}}}>\mathrm{0} \\ $$$$\Rightarrow\:\sqrt{\frac{{p}}{{q}}}+\sqrt{\frac{{q}}{{p}}}+\sqrt{\frac{{c}}{{a}}}\neq\mathrm{0} \\ $$$$ \\ $$$$\frac{{p}}{{q}}=\mathrm{0}\:\Rightarrow\:\frac{{q}}{{p}}\:\mathrm{not}\:\mathrm{defined} \\ $$$$ \\ $$$$\frac{{p}}{{q}}\in\mathbb{R}^{−} \:\Rightarrow\:−\frac{{p}}{{q}}\in\mathbb{R}^{+} \:\Rightarrow\: \\ $$$$\Rightarrow\sqrt{\frac{{p}}{{q}}}=\mathrm{i}\sqrt{−\frac{{p}}{{q}}}\wedge\sqrt{\frac{{q}}{{p}}}=\mathrm{i}\sqrt{−\frac{{q}}{{p}}}\:\Rightarrow \\ $$$$\Rightarrow\:\sqrt{\frac{{p}}{{q}}}+\sqrt{\frac{{q}}{{p}}}=\mathrm{i}{u}\wedge{u}>\mathrm{0} \\ $$$$\sqrt{\frac{{c}}{{a}}}={v}\vee\mathrm{i}{v}\wedge{v}\in\mathbb{R}^{+} \\ $$$$\Rightarrow\:\sqrt{\frac{{p}}{{q}}}+\sqrt{\frac{{q}}{{p}}}+\sqrt{\frac{{c}}{{a}}}\neq\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com