Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 202324 by hardmath last updated on 24/Dec/23

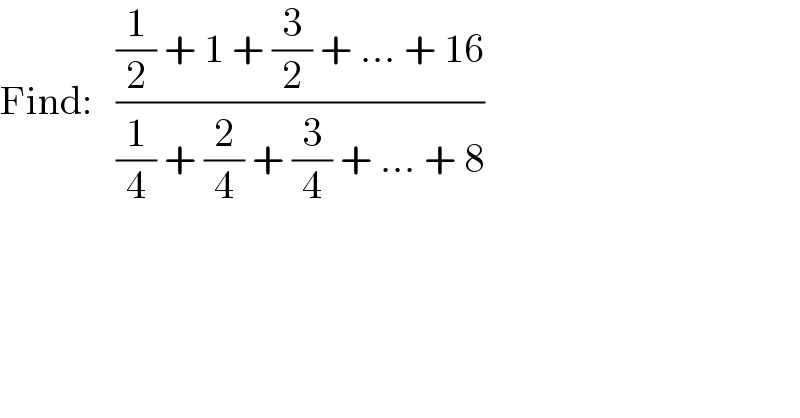
Find: (((1/2) + 1 + (3/2) + ... + 16)/((1/4) + (2/4) + (3/4) + ... + 8))

$$\mathrm{Find}:\:\:\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\:+\:\mathrm{1}\:+\:\frac{\mathrm{3}}{\mathrm{2}}\:+\:...\:+\:\mathrm{16}}{\frac{\mathrm{1}}{\mathrm{4}}\:+\:\frac{\mathrm{2}}{\mathrm{4}}\:+\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:...\:+\:\mathrm{8}} \\ $$

Answered by MATHEMATICSAM last updated on 24/Dec/23

(((1/2) + 1 + (3/2) + .... + 16)/((1/4) + (2/4) + (3/4) + .... + 8)) = (((1/2) + (2/2) + (3/2) + (4/2) + .... + ((32)/2))/((1/4) + (2/4) + (3/4) + (4/4) + .... + ((32)/4))) = (((1/2)[1 + 2 + 3 + 4 + .... + 32])/((1/4)[1 + 2 + 3 + 4 + .... + 32])) = (1/2) × 4 = 2

$$\frac{\frac{\mathrm{1}}{\mathrm{2}}\:+\:\mathrm{1}\:+\:\frac{\mathrm{3}}{\mathrm{2}}\:+\:....\:+\:\mathrm{16}}{\frac{\mathrm{1}}{\mathrm{4}}\:+\:\frac{\mathrm{2}}{\mathrm{4}}\:+\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:....\:+\:\mathrm{8}} \\ $$$$=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{2}}{\mathrm{2}}\:+\:\frac{\mathrm{3}}{\mathrm{2}}\:+\:\frac{\mathrm{4}}{\mathrm{2}}\:+\:....\:+\:\frac{\mathrm{32}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{4}}\:+\:\frac{\mathrm{2}}{\mathrm{4}}\:+\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:\frac{\mathrm{4}}{\mathrm{4}}\:+\:....\:+\:\frac{\mathrm{32}}{\mathrm{4}}} \\ $$$$=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{1}\:+\:\mathrm{2}\:+\:\mathrm{3}\:+\:\mathrm{4}\:+\:....\:+\:\mathrm{32}\right]}{\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{1}\:+\:\mathrm{2}\:+\:\mathrm{3}\:+\:\mathrm{4}\:+\:....\:+\:\mathrm{32}\right]} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:×\:\mathrm{4} \\ $$$$=\:\mathrm{2}\: \\ $$

Commented by hardmath last updated on 24/Dec/23

thankyou dear professor/

$$\mathrm{thankyou}\:\mathrm{dear}\:\mathrm{professor}/ \\ $$

Answered by Rasheed.Sindhi last updated on 25/Dec/23

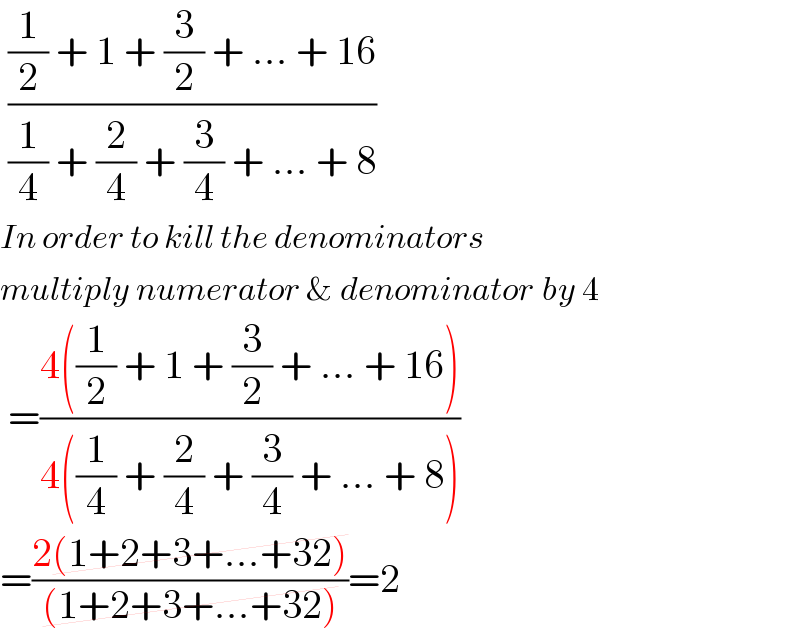
(((1/2) + 1 + (3/2) + ... + 16)/((1/4) + (2/4) + (3/4) + ... + 8)) In order to kill the denominators multiply numerator & denominator by 4 =((4((1/2) + 1 + (3/2) + ... + 16))/(4((1/4) + (2/4) + (3/4) + ... + 8))) =((2(1+2+3+...+32))/((1+2+3+...+32)))=2

$$\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\:+\:\mathrm{1}\:+\:\frac{\mathrm{3}}{\mathrm{2}}\:+\:...\:+\:\mathrm{16}}{\frac{\mathrm{1}}{\mathrm{4}}\:+\:\frac{\mathrm{2}}{\mathrm{4}}\:+\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:...\:+\:\mathrm{8}} \\ $$$${In}\:{order}\:{to}\:{kill}\:{the}\:{denominators} \\ $$$${multiply}\:{numerator}\:\&\:{denominator}\:{by}\:\mathrm{4} \\ $$$$\:=\frac{\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{2}}\:+\:\mathrm{1}\:+\:\frac{\mathrm{3}}{\mathrm{2}}\:+\:...\:+\:\mathrm{16}\right)}{\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{4}}\:+\:\frac{\mathrm{2}}{\mathrm{4}}\:+\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:...\:+\:\mathrm{8}\right)} \\ $$$$=\frac{\mathrm{2}\cancel{\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\mathrm{32}\right)}}{\cancel{\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\mathrm{32}\right)}}=\mathrm{2} \\ $$

Commented by MathematicalUser2357 last updated on 26/Dec/23

denominators isn′t humans

$$\mathrm{denominators}\:\mathrm{isn}'\mathrm{t}\:\mathrm{humans} \\ $$

Commented by Rasheed.Sindhi last updated on 26/Dec/23

😀

😀

Terms of Service

Privacy Policy

Contact: info@tinkutara.com