
Question Number 201352 by cortano12 last updated on 05/Dec/23

$$\:\:\:\mathrm{2023}^{\mathrm{2023}} \:=\:...\:\left(\mathrm{mod}\:\mathrm{13}\right) \\ $$
Answered by Rasheed.Sindhi last updated on 05/Dec/23
![2023^(2023) ≡ ... (mod 13) 2023^(2023) ≡8^(2023) ≡x(mod 13) [∵ 2023≡8(mod 13)] ∵8^4 ≡1(mod 13 ∴ 8^(2023) =(8^4 )^(505) (8^3 )≡8^3 ≡5(mod 13)](Q201360.png)
$$\:\:\:\mathrm{2023}^{\mathrm{2023}} \:\equiv\:...\:\left(\mathrm{mod}\:\mathrm{13}\right) \\ $$$$\mathrm{2023}^{\mathrm{2023}} \\ $$$$\:\:\:\:\:\equiv\mathrm{8}^{\mathrm{2023}} \equiv{x}\left(\mathrm{mod}\:\mathrm{13}\right)\:\:\:\:\:\:\left[\because\:\mathrm{2023}\equiv\mathrm{8}\left(\mathrm{mod}\:\mathrm{13}\right)\right] \\ $$$$\because\mathrm{8}^{\mathrm{4}} \equiv\mathrm{1}\left({mod}\:\mathrm{13}\right. \\ $$$$\therefore\:\mathrm{8}^{\mathrm{2023}} =\left(\mathrm{8}^{\mathrm{4}} \right)^{\mathrm{505}} \left(\mathrm{8}^{\mathrm{3}} \right)\equiv\mathrm{8}^{\mathrm{3}} \equiv\mathrm{5}\left(\mathrm{mod}\:\mathrm{13}\right) \\ $$
Answered by mr W last updated on 05/Dec/23
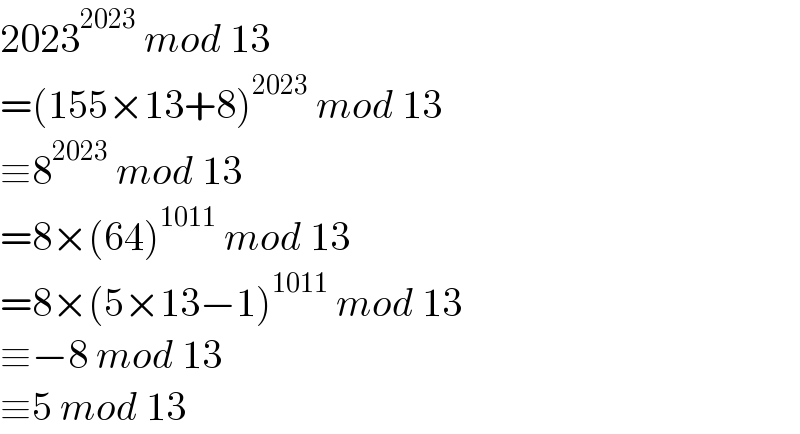
$$\mathrm{2023}^{\mathrm{2023}} \:{mod}\:\mathrm{13} \\ $$$$=\left(\mathrm{155}×\mathrm{13}+\mathrm{8}\right)^{\mathrm{2023}} \:{mod}\:\mathrm{13} \\ $$$$\equiv\mathrm{8}^{\mathrm{2023}} \:{mod}\:\mathrm{13} \\ $$$$=\mathrm{8}×\left(\mathrm{64}\right)^{\mathrm{1011}} \:{mod}\:\mathrm{13} \\ $$$$=\mathrm{8}×\left(\mathrm{5}×\mathrm{13}−\mathrm{1}\right)^{\mathrm{1011}} \:{mod}\:\mathrm{13} \\ $$$$\equiv−\mathrm{8}\:{mod}\:\mathrm{13} \\ $$$$\equiv\mathrm{5}\:{mod}\:\mathrm{13} \\ $$
Answered by BaliramKumar last updated on 05/Dec/23
![2023^(2023) = x (mod13) [φ(13)= 12] (13×155+8)^((12×168+7)) = x(mod13) (8)^((7)) = x(mod13) (8^2 )^3 ×8^1 = x(mod13) (64)^3 ×8^1 = x(mod13) (−1)^3 ×8^1 = x(mod13) −8 = x(mod13) 1×13−8 = x(mod13) 5 = 5(mod13) x = 5](Q201369.png)
$$\mathrm{2023}^{\mathrm{2023}} \:=\:\mathrm{x}\:\left(\mathrm{mod13}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\phi\left(\mathrm{13}\right)=\:\mathrm{12}\right] \\ $$$$\left(\mathrm{13}×\mathrm{155}+\mathrm{8}\right)^{\left(\mathrm{12}×\mathrm{168}+\mathrm{7}\right)} \:=\:\mathrm{x}\left(\mathrm{mod13}\right) \\ $$$$\left(\mathrm{8}\right)^{\left(\mathrm{7}\right)} \:=\:\mathrm{x}\left(\mathrm{mod13}\right) \\ $$$$\left(\mathrm{8}^{\mathrm{2}} \right)^{\mathrm{3}} ×\mathrm{8}^{\mathrm{1}} \:=\:\mathrm{x}\left(\mathrm{mod13}\right) \\ $$$$\left(\mathrm{64}\right)^{\mathrm{3}} ×\mathrm{8}^{\mathrm{1}} \:=\:\mathrm{x}\left(\mathrm{mod13}\right) \\ $$$$\left(−\mathrm{1}\right)^{\mathrm{3}} ×\mathrm{8}^{\mathrm{1}} \:=\:\mathrm{x}\left(\mathrm{mod13}\right) \\ $$$$−\mathrm{8}\:=\:\mathrm{x}\left(\mathrm{mod13}\right) \\ $$$$\mathrm{1}×\mathrm{13}−\mathrm{8}\:=\:\mathrm{x}\left(\mathrm{mod13}\right) \\ $$$$\mathrm{5}\:=\:\mathrm{5}\left(\mathrm{mod13}\right) \\ $$$$\mathrm{x}\:=\:\mathrm{5} \\ $$
